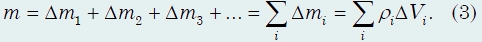
Обратите внимание на проведенные рассуждения о плотности неоднородного тела. Масса тела − характеристика конкретного тела, неважно, из чего оно сделано, является ли оно однородным или состоит из частей, изготовленных из различных материалов. Можно сказать, что масса характеризует тело целиком. Плотность же есть характеристика вещества, из которого изготовлено данное тело или его часть. Иными словами, плотность − «точечная» характеристика в том смысле, что мы приписываем эту характеристику каждой точке тела.
Вспомните наши рассуждения о переходе от средней к мгновенной скорости. Тогда мы критиковали, с физической точки зрения, понятие мгновенной (в математическом смысле) скорости как неизмеримую, в принципе, физическую величину. Аналогичные претензии можно высказать и по поводу «точечной» плотности. Не имеет смысла говорить о сколь угодно малом объеме вещества − все тела состоят из атомов и молекул. Поэтому малость объема ограничена, по крайней мере, размером атома. Тем не менее понятие плотности оказывается удобным для описания распределения масс внутри тела − математическая простота окупает определенные логические проблемы. Поэтому мы и в данном случае, и во многих других будем пользоваться подобными «точечными» характеристиками веществ и процессов. Часто такой подход объясняют введением своеобразного физико-математического «кентавра». Будем называть ΔV физически малым объемом, малым, с математической точки зрения, настолько, что можно пользоваться анализом2бесконечно малых величин, и достаточно большим, чтобы содержать значительное число атомов и молекул. 1Именно так определял массу И. Ньютон.
2Более точно − интегральным и дифференциальным исчислением, но не пугайтесь − мы обойдемся без этого замечательного раздела математики.
7. Законы Ньютона и их применение. Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любоймеханической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированыИсааком Ньютоном в книге «Математические начала натуральной философии» (1687 год). Первый закон Ньютона Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как Закон инерции. Инерция — это свойство тела сохранять свою скорость движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают разной инертностью. Инертность — это свойство тел сопротивляться изменению их скорости. Величина инертности характеризуется массой тела. Современная формулировка В современной физике первый закон Ньютона принято формулировать в следующем виде: | Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакиесилы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. |
Историческая формулировка Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде: Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. | С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета. |
 Скачать 5.42 Mb.
Скачать 5.42 Mb.