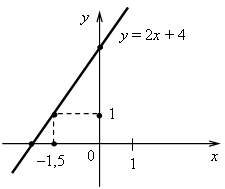Домашняя работа. Домашняя контрольная работа. 1. Функция задана формулой

• Название: 1. Функция задана формулой
• Анкор: Домашняя работа
• Дата: 24.07.2022
• Размер: 56.39 Kb.
• Имя файла: Домашняя контрольная работа.docx
• Тип: Документы; #635490

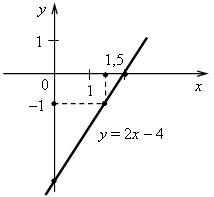
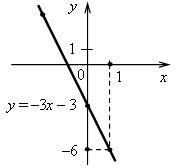
Вариант 1

1. Функция задана формулой у = 6х + 19. Определите:

а) значение у, если х = 0,5;

б) значение х, при котором у = 1;

в) проходит ли график функции через точку А (–2; 7).

2. а) Постройте график функции у = 2х – 4.

б) Укажите с помощью графика, чему равно значение у при х = 1,5.

3. В одной и той же системе координат постройте графики функций:

а) у = –2х; б) у = 3.

4. Найдите координаты точки пересечения графиков функций
у = 47х – 37 и у = –13х + 23.

5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.

Вариант 2

1. Функция задана формулой у = 4х – 30. Определите:

а) значение у, если х = –2,5;

б) значение х, при котором у = –6;

в) проходит ли график функции через точку В (7; –3).

2. а) Постройте график функции у = –3х + 3.

б) Укажите с помощью графика, при каком значении х значение у равно 6.

3. В одной и той же системе координат постройте графики функций:

а) у = 0,5х; б) у = –4.

4. Найдите координаты точки пересечения графиков функций
у = –38х + 15 и у = –21х – 36.

5. Задайте формулой линейную функцию, график которой параллелен прямой
у = –5х + 8 и проходит через начало координат.
Вариант 3

1. Функция задана формулой у = 5х + 18. Определите:

а) значение у, если х = 0,4;

б) значение х, при котором у = 3;

в) проходит ли график функции через точку С (–6; –12).

2. а) Постройте график функции у = 2х + 4.

б) Укажите с помощью графика, чему равно значение у при х = –1,5.

3. В одной и той же системе координат постройте графики функций:

а) у = –0,5х; б) у = 5.

4. Найдите координаты точки пересечения графиков функций
у = –14х + 32 и у = 26х – 8.

5. Задайте формулой линейную функцию, график которой параллелен прямой
у = 2х + 9 и проходит через начало координат.
Вариант 4

1. Функция задана формулой у = 2х – 15. Определите:

а) значение у, если х = –3,5;

б) значение х, при котором у = –5;

в) проходит ли график функции через точку K (10; –5).

2. а) Постройте график функции у = –3х – 3.

б) Укажите с помощью графика, при каком значении х значение у равно –6.

3. В одной и той же системе координат постройте график функций:

а) у = 2х; б) у = –4.

4. Найдите координаты точки пересечения графиков функций
у = –10х – 9 и у = –24х + 19.

5. Задайте формулой линейную функцию, график которой параллелен прямой у = –8х + 11 и проходит через начало координат.
Вариант 1

1. Функция задана формулой у = 6х + 19. Определите:

а) значение у, если х = 0,5;

б) значение х, при котором у = 1;

в) проходит ли график функции через точку А (–2; 7).

2. а) Постройте график функции у = 2х – 4.

б) Укажите с помощью графика, чему равно значение у при х = 1,5.

3. В одной и той же системе координат постройте графики функций:

а) у = –2х; б) у = 3.

4. Найдите координаты точки пересечения графиков функций
у = 47х – 37 и у = –13х + 23.

5. Задайте формулой линейную функцию, график которой параллелен прямой
у = 3х – 7 и проходит через начало координат.

Вариант 2

1. Функция задана формулой у = 4х – 30. Определите:

а) значение у, если х = –2,5;

б) значение х, при котором у = –6;

в) проходит ли график функции через точку В (7; –3).

2. а) Постройте график функции у = –3х + 3.

б) Укажите с помощью графика, при каком значении х значение у равно 6.

3. В одной и той же системе координат постройте графики функций:

а) у = 0,5х; б) у = –4.

4. Найдите координаты точки пересечения графиков функций
у = –38х + 15 и у = –21х – 36.

5. Задайте формулой линейную функцию, график которой параллелен прямой
у = –5х + 8 и проходит через начало координат.

Решение заданий контрольной работы

Вариант 1

1. у = 6х + 19.

а) Если х = 0,5, то у = 6 · 0,5 + 19 = 3 + 19 = 22;

б) если у = 1, то 6х + 19 = 1;

6х = 1 – 19;

6х = –18;

х = –18 : 6;

х = –3;

в) 7 = 6 · (–2) + 19;

7 = –12 + 19;

7 = 7 – верно, значит, график функции проходит через точку
А (–2; 7).

Ответ: а) 22; б) –3; в) проходит.

2. а) у = 2х – 4. Построим две точки, принадлежащие графику. Если х = 0, то у = 2 · 0 – 4 = –4; если х = 2, то у = 2 · 2 – 4 = 0. (0; –4), (2; 0). б) При х = 1,5 у = –1.
3. а) у = –2х. Графиком является прямая, проходящая через начало координат и точку (2; –4). б) у = 3. Графиком является прямая, проходящая через точку (0; 3) и параллельная оси х. 4. Решим уравнение: 47х – 37 = –13х + 23. 47х + 13х = 23 + 37;

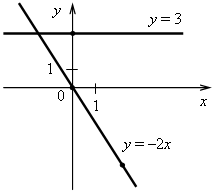
60х = 60;

х = 1, значит, абсцисса точки пересечения графиков функций равна 1. Найдем соответствующее значение ординаты:

если х = 1, то у = 47 · 1 – 37 = 10.

Точка пересечения имеет координаты (1; 10).

Ответ: (1; 10).

5. График параллелен прямой у = 3х – 7, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 3х.

Ответ: у = 3х.

Вариант 2

1. у = 4х – 30.

а) Если х = –2,5, то у = 4 · (–2,5) – 30 = –10 – 30 = –40;

б) если у = –6, то 4х – 30 = –6;

4х = –6 + 30;

4х = 24;

х = 24 : 4;

х = 6;

в) –3 = 4 · 7 – 30;

–3 = 28 – 30;

–3 = –2 – неверно, значит, график функции не проходит через точку В (7; –3).

Ответ: а) –40; б) 6; в) не проходит.

2. а) у = –3х + 3. Построим две точки, принадлежащие графику. Если х = 0, то у = –3 · 0 + 3 = 3; если х = 2, то у = –3 · 2 + 3 = –3; (0; 3), (2; –3) б) Если у = 6, то х = –1.

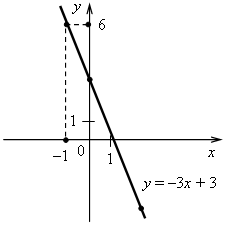
3. а) у = 0,5х. Графиком является прямая, проходящая через начало координат и точку (4; 2).

б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.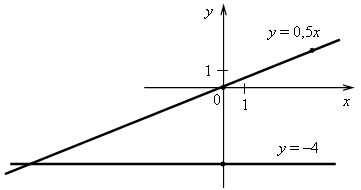



4. Решим уравнение:

–38х + 15 = –21х – 36;

–38х + 21х = –36 – 15;

–17х = –51;

х = (–51) : (–17);

х = 3, значит, абсцисса точки пересечения графиков функций равна 3.

Найдем соответствующее значение ординаты:

если х = 3, то у = –38 · 3 + 15 = –99.

Точка пересечения имеет координаты (3; –99).

Ответ: (3; –99).

5. График параллелен прямой у = –5х + 8, значит, угловые координаты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = –5х.

Ответ: у = –5х.

Вариант 3

1. у = 5х + 18.

а) Если х = 0,4, то у = 5 · 0,4 + 18 = 2 + 18 = 20;

б) если у = 3, то 5х + 18 = 3;

5х = 3 – 18;

5х = –15;

х = –15 : 5;

х = –3;

в) –12 = 5 · (–6) + 18;

–12 = –30 + 18;

–12 = –12 – верно, значит, график функции проходит через точку
С (–6; –12).

Ответ: а) 20; б) –3; в) проходит.

2. а) у = 2х + 4. Построим две точки, принадлежащие графику. Если х = 0, то у = 2 · 0 + 4 = 4; если х = –2, то 2 · (–2) + 4 = 0. (0; 4), (–2; 0) б) Если х = –1,5, то у = 1.

3. а) у = –0,5х. Графиком является прямая, проходящая через начало координат и точку (4; –2).

б) у = 5. Графиком является прямая, проходящая через точку (0; 5) и параллельная оси х.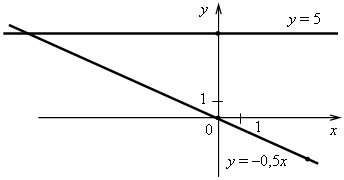



4. Решим уравнение:

–14х + 32 = 26х – 8;

–14х – 26х = –8 – 32;

–40х = –40;

х = 1, значит, абсцисса точки пересечения графиков равна 1. Найдем соответствующее значение ординаты:

если х = 1, то у = –14 · 1 + 32 = 18.

Точка пересечения имеет координаты (1; 18).

Ответ: (1; 18).

5. График параллелен прямой у = 2х + 9, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это прямая пропорциональность. Значит, у = 2х.

Ответ: у = 2х.

Вариант 4

1. у = 2х – 15.

а) Если х = –3,5, то у = 2 · (–3,5) – 15 = –7 – 15 = –22;

б) если у = –5, то 2х – 15 = –5;

2х = –5 + 15;

2х = 10;

х = 5;

в) –5 = 2 · 10 – 15;

–5 = 20 – 15;

–5 = 5 – неверно, значит, график функции не проходит через точку
K (10; –5).

Ответ: а) –22; б) 5; в) не проходит.

2. а) у = –3х – 3. Построим две точки, принадлежащие графику: если х = 0, то у = –3 · 0 – 3 = –3; если х = –2, то у = (–3) · (–2) – 3 = 3. (0; –3), (–2; 3). б) Если у = –6, то х = 1.
3. а) у = 2х. Графиком является прямая, проходящая через начало координат и точку (2; 4). б) у = –4. Графиком является прямая, проходящая через точку (0; –4) и параллельная оси х.

4. Решим уравнение:

–10х – 9 = –24х + 19;

–10х + 24х = 19 + 9;

14х = 28;

х = 28 : 14;

х = 2, значит, абсцисса точки пересечения графиков равна 2. Найдем соответствующее значение ординаты:

если х = 2, то у = –10 · 2 – 9 = –29.

Точка пересечения имеет координаты (2; –29).

Ответ: (2; –29).

5. График параллелен прямой у = –8х + 11, значит, угловые коэффициенты равны. Так как прямая проходит через начало координат, то это – прямая пропорциональность. Значит, у = –8х.

Ответ: у = –8х.