вопросы. 5) Вопросы для зачета (1). 1. Группировка исходных данных в ппп statistica
 Скачать 105.3 Kb. Скачать 105.3 Kb.
|
|
Вопросы к зачету (закрепление компетенций ОПК-4 ПК- 2 ПК-8): 1. Группировка исходных данных в ППП Statistica. ППП STATISTICA – это универсальная интегрированная система, предназначенная для статистического анализа и обработки данных. Содержит многофункциональную систему для работы с данными, широкий набор статистических модулей, в которых собраны группы логически связанных между собой статистических процедур, специальный инструментарий для подготовки отчетов, мощную графическую систему для визуализации данных, систему обмена данными с другими Windows-приложениями. Группировка, в которой для характеристики групп применяется численность группы, называется рядом распределения. Ряд распределения состоит из двух элементов: варианты – отдельного значения варьирующего признака, которое он принимает в ряду распределения, и частоты – численность отдельных вариант, т.е. частота повторения каждой варианты. Если частота выражена в долях единицы или в процентах к итогу (к общей сумме частот), то это – частость. В пакете STATISTICA широкие возможности по проведению группировки, построению рядов распределения и их графиков предоставляют Frequency tables – Таблицы частот и Tables andbanners -Таблицы и заголовки в меню Analysis-Анализ модуля Basic Statistics and Tables – Основные статистики и таблицы. 2. Непараметрические методы оценки тесноты связи в ППП Statistica. Непараметрические методы статистики – это методы, независящие от характера распределения генеральной совокупности. Этим они отличаются от параметрических методов, к которым относят, например, корреляционно-регрессионный анализ. Именно отсутствие требования о знании закона распределения исследуемых показателей делают непараметрические методы особенно привлекательными и популярными в «западной» статистике. Пакет STATISTICA через диалоговое окно NonparametricStatistics предлагает следующие процедуры: 2x2 Tables–выявление связи между двумя качественными альтернативными признаками. ObservedversusexpectedXi – проверка согласия наблюдаемых и ожидаемых частот. Ожидаемые частоты – это частоты, вычисленные на основе предполагаемого закона распределения случайной величины. Correlations – выявление связи между двумя количественными признаками (коэффициенты ранговой корреляции Спирмена и Кендэла, гамма-коэффициент). Comparingtwoindependentsamples – проверка гипотезы о том, что две группы данных представляют собой случайные независимые выборки из одной генеральной совокупности и имеют равные средние и медианы. Предлагаются критерий серий Вальда Вольфовица (Wald-Wolfowitzrunstest), двухвыборочный тест Колмогорова-Смирного (Kolmogorov-Smirnovtwo-sampetest), критерий Манна-Уитни (Mann-WhitneyUtest). Comparingmultipleindep. samples – проверка гипотезы о том, что несколько выборок получены из одной генеральной совокупности. Используется критерий Краскела-Уоллиса (Summary: Kruskal-WallisANOVA). Comparingtwodependentsamples – проверка гипотезы об однородности генеральных совокупностей попарно связанным выборкам (например, сравнение работы двух одинаковых приборов). Предлагаются критерий знаков (Signtest) и критерий Вилкоксона (Wilcoxonwatchedpairtest). Comparingmultipledep. samples – двухфакторный анализ Фридмана и коэффициент конкордации Кендэла (Summary: Friedman ANOVA; Kendall'sconcordance). Проверяется гипотеза о том, что связанные выборки принадлежат однородным генеральным совокупностям. Коэффициент конкордацииКендэла показывает меру связи. Широко используется при оценке согласованности мнений экспертов. CochranQtest – Q-критерий Кохрена используется для анализа связанных выборок, содержащих значения качественного альтернативного признака. 3. Проведение многомерной группировки методом кластерного анализа в среде ППП Statistica. В программе STATISTICA реализованы агломеративные методы минимальной дисперсии – древовидная кластеризация и двухвходовая кластеризация, а также дивизивный метод k-средних. В методе древовидной кластеризации предусмотрены различные правила иерархического объединения в кластеры 1. Правило одиночной связи. На первом шаге объединяются два наиболее близких объекта, т.е. имеющие максимальную меру сходства. На следующем шаге к ним присоединяется объект с максимальной мерой сходства с одним из объектов кластера, т.е. для его включения в кластер требуется максимальное сходство лишь с одним членом кластера. Метод называют еще методом ближайшего соседа, так как расстояние между двумя кластерами определяется как расстояние между двумя наиболее близкими объектами в различных кластерах. Это правило «нанизывает» объекты для формирования кластеров. Недостаток данного метода – образование слишком больших продолговатых кластеров. 2. Правило полных связей. Метод позволяет устранить недостаток, присущий методу одиночной связи. Суть правила в том, что два объекта, принадлежащих одной и той же группе (кластеру), имеют коэффициент сходства, который больше некоторого порогового значения S. В терминах евклидова расстояния это означает, что расстояние между двумя точками (объектами) кластера не должно превышать некоторого порогового значения d. Таким образом, d определяет максимально допустимый диаметр подмножества, образующего кластер. Этот метод называют еще методом наиболее удаленных соседей, так как при достаточно большом пороговом значении d расстояние между кластерами определяется наибольшим расстоянием между любыми двумя объектами в различных кластерах. 3. Правило невзвешенного попарного среднего. Расстояние между двумя кластерами определяется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные группы, однако он работает одинаково хорошо и в случаях протяженных (цепочного типа) кластеров. 4. Правило взвешенное попарное среднее. Метод идентичен предыдущему, за исключением того, что при вычислении размер соответствующих кластеров используется в качестве весового коэффициента. Желательно этот метод использовать, когда предполагаются неравные размеры кластеров. 5. Невзвешенный центроидный метод. Расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. 6. Взвешенный центроидный метод. Идентичен предыдущему, за исключением того, что при вычислениях расстояния используют веса для учета разности между размерами кластеров. Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего. 7. Правило Уорда (Варда). В этом методе в качестве целевой функции применяют внуригрупповую сумму квадратов отклонений, которая есть не что иное, как сумма квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект. На каждом шаге объединяются такие два кластера, которые приводят к минимальному увеличению целевой функции, т.е. внутригрупповой суммы квадратов отклонений. Этот метод направлен на объединение близко расположенных кластеров. Замечено, что метод Уорда приводит к образованию кластеров примерно равных размеров и имеющих форму гиперсфер. 4. Наивные модели прогнозирования. «Наивная» модель прогнозирования предполагает, что последний период прогнозируемого временного ряда лучше всего описывает будущее этого ряда. В таких моделях прогноз, как правило, является довольно простой функцией от наблюдений прогнозируемой величины в недалеком прошлом. Простейшая модель описывается выражением: y(t+1)=y(t),где y(t) - последнее наблюдаемое значение, y(t+1) - прогноз. Данная модель не только не учитывает закономерности прогнозируемого процесса (что в той или мной степени свойственно многим статистическим методам прогнозирования), но и не защищена от случайных изменений в данных, а также не отражает сезонные колебания частоты и тренды.5. Оценивание и анализ парной линейной регрессии. Парная линейная регрессия описывается уравнением: 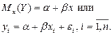 Для получения оценки параметров линейной функции регрессии взята выборка, состоящая из векторных переменных (xi, yi). Оценкой записанной выше модели является уравнение 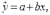 где где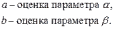 Классический подход к оцениванию параметров α и β основан на классическом (обычном или традиционном) методе наименьших квадратов (МНК). Чтобы регрессионный анализ давал достоверные результаты необходимо выполнить 4условия Гаусса - Маркова:  1. M(εi) = 0 – остатки имеют нулевое среднее для всех i = 1,…, n. 2. D(εi) = σ2 = const для всех i = 1,…, n – гомоскедастичность остатков, то есть их равноизменчивость. 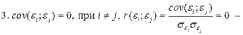 – отсутствие автокорреляции в остатках. 4. Объясняющая переменная X детерминирована, а объясняемая переменная Y – случайная величина и остатки не коррелируют с X: 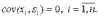 Объясняющая переменная в том случае, когда она стоит в уравнении регрессии, может называться регрессором. Наряду с этими четырьмя условиями Гаусса - Маркова применяют 5-е условие: остатки должны быть распределены нормально; это условие необходимо для обеспечения правильного оценивания значимости уравнения регрессии и его параметров. Наилучшие оценки называют BLUE – оценками (Best Linear Unbiased Estimators). Они обладают следующими свойствами: 1. Это оценки несмещённые: 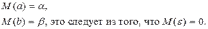 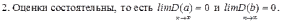 3. Оценки эффективны, то есть имеют наименьшие дисперсии среди всех возможных оценок. Если нарушаются 2-е и/или 3-е условия Гаусса – Маркова, то оценки не теряют свойства 1и 2, а свойство 3 (эффективность) теряют; дисперсии становятся смещёнными. 6. Оценивание и анализ парной нелинейной регрессии. Парная нелинейная регрессия применяется для описания нелинейных видов зависимостей результирующего фактора (у) от одного независимого фактора (.х). В общем случае такие регрессии принято делить на две группы: 1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные но оцениваемым параметрам; 2) регрессии, нелинейные по оцениваемым параметрам. К первой группе относятся следующие функции: • полиномы разных степеней у = а + Ьхх + Ь^х2 + 63х3+ ... • равносторонняя гипербола у = а + Ь/х. Ко второй группе относятся следующие функции: • степенная у = ахР • показательная у = аЪх • экспоненциальная у = еа+Ьх. Функции первой группы достаточно просто сводятся к линейным, например заменой переменных. Их параметры находятся методом наименьших квадратов Функции второй группы принято делить на две подгруппы: • внутренне линейные, которые могут быть приведены к линейному виду путем математических преобразований; • внутренне нелинейные, которые не могут быть сведены к линейному виду. 7. Оценивание и анализ множественной линейной регрессии. Множественная линейная регрессия - выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X1, X2, ..., Xm. Величину Y принято называть зависимой или результирующей переменной, а величины X1, X2, ..., Xm - независимыми или объясняющими переменными. В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель 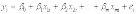 , ,где 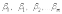 - коэффициенты функции линейной регрессии генеральной совокупности, - коэффициенты функции линейной регрессии генеральной совокупности,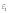 - случайная ошибка. - случайная ошибка.Функция множественной линейной регрессии для выборки имеет следующий вид: 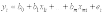 , ,где 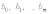 - коэффициенты модели регрессии выборки, - коэффициенты модели регрессии выборки,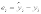 - ошибка. - ошибка.8. Оценивание и анализ множественной нелинейной регрессии. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: - регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; - регрессии, нелинейные по оцениваемым параметрам. Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: - полиномы разных степеней - 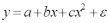 , , 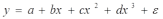 , … (анализ издержек от объема выпуска); , … (анализ издержек от объема выпуска);- равносторонняя гипербола - 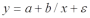 (зависимость между объемом выпуска и средними фиксированными издержками, между доходом и спросом на блага, между уровнем безработицы и процентным изменением заработной платы). (зависимость между объемом выпуска и средними фиксированными издержками, между доходом и спросом на блага, между уровнем безработицы и процентным изменением заработной платы).К нелинейным регрессиям по оцениваемым параметрам относятся функции: - степенная - 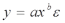 (зависимость между расходами и прибылью); (зависимость между расходами и прибылью);- показательная - 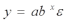 (производственная функция Кобба-Дугласа); (производственная функция Кобба-Дугласа);- экспоненциальная - 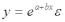 (при анализе изменений переменной с постоянным темпом прироста). (при анализе изменений переменной с постоянным темпом прироста).Нелинейные регрессии по включаемым переменным позволяют использовать МНК для оценки параметров, так как эти функции линейны по параметрам. Рассмотрим параболу 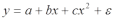 . Введем замену: . Введем замену: 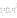 . Получим: . Получим: 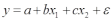 - уравнение множественной линейной регрессии. Парабола 2-й степени целесообразна к применению. Если для определенного интервала значений фактора меняется характер связи признаков: прямая связь меняется на обратную или наоборот. Кривая, для которой b > 0, c < 0 используется при изучении зависимости з/п работников физического труда от возраста. При b < 0, c > 0 – зависимость затрат на производство от объема выпуска. Часто можно использовать лишь сегмент параболы. - уравнение множественной линейной регрессии. Парабола 2-й степени целесообразна к применению. Если для определенного интервала значений фактора меняется характер связи признаков: прямая связь меняется на обратную или наоборот. Кривая, для которой b > 0, c < 0 используется при изучении зависимости з/п работников физического труда от возраста. При b < 0, c > 0 – зависимость затрат на производство от объема выпуска. Часто можно использовать лишь сегмент параболы.9. Применение многофакторных моделей в статистическом анализе. Многофакторные индексные модели можно применить при проведении факторного анализа различных сторон работы АПК: при изучении эффективности использования сельскохозяйственных земель, средств производства, рабочей силы, капитальных вложений; при анализе динамики производительности труда. Общие принципы построения многофакторных индексных моделей. 1. при построении необходимо руководствоваться экономическим содержанием показателей. 2. должна существовать возможность агрегации модели, т.е. полная модель должна распадаться на части. 3. все факторы в модели должны располагаться так, чтобы любые объединения внутри факторов внутри модели давали реальные экономические показатели. 10. Применение многофакторных моделей прогнозирования Множественная корреляция исследует статистическую зависимость результативного признака от нескольких факторных признаков. В общем виде уравнение регрессии имеет вид: 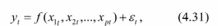 где / = 1,2,...и - количество наблюдений, р - количество параметров, st - возмущающая переменная. Для линейной зависимости 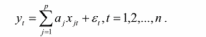 Выбор уравнения множественной регрессии включает следующие этапы: • отбор факторов-аргументов; • выбор уравнения связи; • определение числа наблюдений, необходимых для получения несмещенных оценок. Одним из важнейших требований является отбор наиболее существенных факторов. Также необходим традиционный экономический анализ, в ходе которого глубже и полнее выявляется существо, направленность и теснота связи между факторами. Последовательное введение всех конкурирующих факторов в уравнение регрессии следует осуществлять с точки зрения минимизации остаточной дисперсии. В процессе отбора факторных признаков особое внимание следует уделять выявлению и устранению мультиколлинсарности - тесной корреляционной связи между двумя (коллинеарности) и большим числом факторных признаков. Если в модель включаются две или несколько связанных между собой «независимых» переменных, то система нормальных уравнений не имеет однозначного решения, наряду с уравнением регрессии существуют и другие линейные соотношения. Последствия мультиколлинеарности: слабая обусловленность матрицы системы нормальных уравнений; неопределенное множество коэффициентов регрессии; сильная корреляция стандартных ошибок параметров и возрастание остаточных дисперсий; чувствительность коэффициентов регрессии к выборке. 11. Трендовые модели прогнозирования Трендовая модель наиболее популярна в прогнозировании. Она основана на том, что объем и особенно структура спроса характеризуются определенной степенью инерционности, т.е. потребление с запаздыванием приспосабливается к изменившимся условиям. Инерционность означает в данном случае невозможность произвольно в короткое время существенно изменить не только структуру, но и привычки потребления населения. Трендовая модель прогнозирования - это уравнение, формализующее закономерности развития спроса в базисном периоде. Модель применяется в том случае, если установлено, что найденные закономерности будут действовать на определенном отрезке времени в будущем. В этом случае ряд динамики рассматривается как функция времени и с известным приближением описывается различными математическими уравнениями. Из трендовых моделей в прогнозировании спроса наиболее широко используются следующие виды: а) уравнение прямой y = a + bx, (2.2) б) логарифмическая функция y = a + blgx, (2.3) в) экспоненциальная функция y = ax, (2.4) г) параболическая функция y = a + bx + cx (2.5) д) логистическая функция Прогноз спроса на базе трендовых моделей основывается на допущении, что все факторы, действовавшие в базисном периоде, и взаимосвязь этих факторов останутся неизменными и в прогнозном периоде. Однако такое условие в жизни часто нарушается. Поэтому метод трендовых моделей в прогнозировании спроса можно применять с упреждением на один, максимум на два интервала динамического ряда с детальным учетом всех факторов, влияющих на формирование покупательского спроса. В таком явлении, как спрос, когда наблюдается одновременное влияние многих разнородных факторов, тесно взаимодействующих друг с другом, довольно трудно создать точную модель с хорошо интерпретирующими функциональными связями. 12. Прогнозирование на основе методов усреднения В данном подходе прогнозирования, все будущие значения принимаются равными средним значениям исторических данных. Этот подход может быть использован для любых исторических данных. Метод усреднения позволяет разработать прогноз, основываясь на среднем значении прошлых наблюдений. 13. Прогнозирование на основе методов сглаживания динамических рядов Одной из задач анализа рядов динамики, является установление закономерностей изменения уровней изучаемого показателя во времени. В некоторых случаях эта закономерность развития объекта вполне ясно отображается уровнями динамического ряда. Однако часто приходится встречаться с такими рядами динамики, когда уровни ряда претерпевают самые различные изменения. В подобных случаях для определения основной тенденции развития, достаточно устойчивой на протяжении данного периода, используют особые приёмы обработки рядов динамики. Уровни ряда динамики формируются под совокупным влиянием множества длительных и кратковременных факторов, в том числе различных, случайных обстоятельств. В то же время выявление основной тенденции изменения уровня ряда предполагает её количественное выражение, которое свободно от случайных воздействий. Существуют различные методы выявления тенденции развития динамики. Одним из приёмов выявления основной тенденции является метод укрупнения интервалов. Этот способ основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. 14. Прогнозирование периодических колебаний Во многих временных рядах проявляется сезонный фактор в виде периодических регулярных колебаний, причем период таких колебаний не превышает года и равен кварталу, месяцу или неделе. Пусть выбрана аддитивная модель ряда. Представляется, что невозможно установить полностью объективное правило, разделяющее тренд и сезонность. Однако те или иные методы позволяют приближенно оценить сезонные колебания. Простейший путь оценки сезонности для ряда y1, y2, ..., yt, ..., yn с периодом сезонности l (l=12 для ежемесячных данных, l =4 для ежеквартальных данных) заключается в вычислении разности (отношения) между средним по всем одноименным месяцам (кварталам) и средним по всем данным. В результате получаем сезонную компоненту неизменную во времени. Если временной ряд содержит выраженную тенденцию развития, то перед выделением сезонных колебаний сначала должен быть выделен тренд. Обозначим число целых периодов h=n/l, тогда: 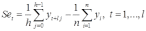 . .Если в последней формуле вычитание заменяется отношением, то получим так называемый индекс сезонности. Альтернативный метод оценивания сезонной волны состоит в выделении тренда скользящими средними, например, по формуле (m=l/2): 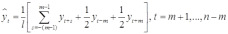 , ,и использовании отклонений от сглаженных значений в качестве оценок сезонности: 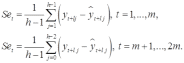 (9.30) (9.30)Если выбирается мультипликативная модель ряда, то в последней формуле вместо разностей берется отношение. Разные пределы суммирования объясняются тем, что при использовании скользящей средней с четным значением длины интервала сглаживания m первых и m последних уровней будут потеряны. Затем полученные значения сезонной компоненты корректируются так, чтобы суммарное воздействие сезонности на динамику было нейтральным. В случае аддитивной модели сумма значений сезонной составляющей для одного периода должна быть равна нулю. Поэтому окончательные оценки сезонности получаются по формуле: 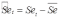 , t=1,…,l, (9.31) , t=1,…,l, (9.31)где 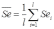 . В случае мультипликативной модели: . В случае мультипликативной модели: 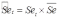 , , 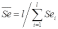 . .15. Прогнозирование спроса и предложения Прогнозы спроса и предложения составляют, используя методы планирования человеческих ресурсов и техники моделирования. В крупных организациях использование моделирования приносит особенно хорошие плоды, поскольку позволяет провести анализ чувствительности воздействия различных предположений относительно будущего (т. е. ответить на вопросы типа «А что, если?..»). Там, где существуют обширные базы данных относительно потока, требования к атрибутам (спецификации сотрудников) и оценки показателей труда и потенциала, можно пользоваться экспертными системами. Подобные системы позволяют установить отношения между возможностями и свойствами личности, которые необходимы для использования этих возможностей, поэтому консультанты по вопросам карьеры могут взять набор личностных характеристик и определить, какие возможности больше всего подходят для данного конкретного человека. На стадии планирования карьеры они могут также выявить людей с нужными способностями и навыками для конкретных рабочих мест и предоставить информацию относительно программ управления карьерой, которые обеспечат соответствие атрибутов и рабочих мест и развитие карьеры с надлежащей скоростью. Для этой цели были специально разработаны такие системы управления карьерой, как ExecuGROW (Control Data). Однако и у сложности есть предел. Существует так много переменных и непредсказуемых изменений факторов, как спроса, так и предложения, что можно проводить лишь ежегодную проверку, чтобы увидеть, какая взаимосвязь существует между числом менеджеров, которые определенно уйдут на пенсию в течение ближайших четырех-пяти лет, и количеством менеджеров, стоящих на ступеньку ниже, которые станут их преемниками. Если сравнение этих данных выявит серьезный дисбаланс, то необходимо предпринять шаги, направленные на уменьшение или устранение дефицита, или рассмотреть другие возможности использования тех, кто вряд ли пойдет на повышение. 16. Прогнозирование и анализ экономического роста на основе модели производственной функции Кобба-Дугласа Одной из важнейших проблем при анализе экономического роста является определение вклада каждого производственного вклада в увеличение выпуска продукции. Решение этой проблемы важно для определения оптимального сочетания факторов производства, обеспечивающего увеличение темпов экономического роста. В качестве инструмента факторного анализа обеспечения экономического роста в большинстве современных моделей используется производственная функция, отражающая связь не только между величиной выпуска и затратами факторов производства, но и уровнем технологического развития. Впервые такая модель была предложена в 20-х гг. XX века американским экономистом П.Дугласом и математиком Х.Коббом. Производственная функция Кобба-Дугласа является частным случаем производственной функции (1) и имеет следующий вид: 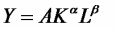 , (6) , (6)где: 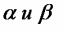 – коэффициенты эластичности объема выпуска по затратам, капитала (K) и труда (L) соответственно; – коэффициенты эластичности объема выпуска по затратам, капитала (K) и труда (L) соответственно;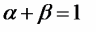 . .Параметры 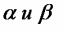 были определены авторами в результате эмпирического исследования обрабатывающей промышленности в США и составляют 0,25 и 0,75 соответственно. были определены авторами в результате эмпирического исследования обрабатывающей промышленности в США и составляют 0,25 и 0,75 соответственно.Это означает, что повышение затрат капитала (K) на 1% вызовет рост выпуска продукции (Y) на 0,25%, а повышение затрат труда (L) на 1% вызовет рост выпуска продукции на 0,75%. Таким образом, вклад труда в ВВП в три раза больше вклада физического капитала. Модель Кобба-Дугласа позволяет подойти к измерению вклада технологического прогресса (A) в экономический рост. Если уравнение (6) переписать в темпах прироста выпуска, то получим следующую формулу: 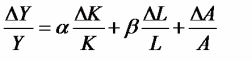 , (7) , (7)где: 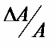 – показывает вклад прироста совокупной производительности факторов K и L, т.е. вклад технологического прогресса. – показывает вклад прироста совокупной производительности факторов K и L, т.е. вклад технологического прогресса.17. Подбор стационарной модели ARIMA для ряда наблюдений Структура модели ARIMA описывается тремя параметрами (р, q, k). Кроме того, разные по форме модели могут быть довольно близки друг другу. Поэтому весьма важно по возможности правильно определить структуру модели. Рассмотрим этапы идентификации. 1. Подбирается порядок модели k. Для этого используется либо метод последовательных разностей, либо анализ автокорреляционных функций процессов Dy(t), D2y(t), … - пока не достигнем быстрого затухания (стационарности) автокорреляционной функции для некоторого k. Дж.Бокс и Г.Дженкинс предлагают взять за визуальный критерий стационарности быстрое убывание значений выборочной АКФ. Использование завышенного порядка разности приводит к росту дисперсии ошибок и к заметному росту дисперсии прогноза. 2. Находим yk(t)=Dky(t) и идентифицируем ARMA(р, q) модель. 18. Нестационарные ARIMA модели В случае, когда временной ряд не является стационарным, необходимо оценить и исключить из временного ряда нестационарные особенности, прежде чем минимизировать ожидаемые потери в задаче (1). Таким образом, прогноз xˆT +1 нестационарного временного ряда будет складываться из двух частей: прогноз нестационарной компоненты xˆ ns T +1 и прогноз стационарной компоненты xˆ s T +1: xˆT +1 = ˆx ns T +1 + ˆx s T +1. Алгоритм прогнозирования нестационарной компоненты временного ряда должен быть таким, чтобы регрессионные остатки при прогнозе доступной для обучения истории x r = {(ri) T i=1 | ri = xi − xˆ ns i } были стационарным временным рядом, значения которого сгенерированы из одного распределения с плотностью γ(u). В качестве алгоритма прогнозирования нестационарной части ряда предлагается использовать ARIMA. Для оптимизации параметров этот алгоритм использует квадратичную функцию потерь Lsq(ˆx, x) = (ˆx − x) 2 , по которой строится функционал потерь: Q(f ns , x) = 1 T X T i=1 Lsq(f ns(w, xi , 1), xi+1); xi = {x1 · · · xi}. 19. Прогнозирование с учетом сезонной составляющей в ППП Excel. Для прогнозирования объема продаж, имеющего сезонный характер, предлагается следующий алгоритм построения прогнозной модели: 1.Определяется тренд, наилучшим образом аппроксимирующий фактические данные. Существенным моментом при этом является предложение использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели. 2.Вычитая из фактических значений объёмов продаж значения тренда, определяют величины сезонной компоненты и корректируют таким образом, чтобы их сумма была равна нулю. 3.Рассчитываются ошибки модели как разности между фактическими значениями и значениями модели. 4.Строится модель прогнозирования: F = T + S ± E где: F– прогнозируемое значение; Т– тренд; S – сезонная компонента; Е - ошибка модели. 5.На основе модели строится окончательный прогноз объёма продаж. Для этого предлагается использовать методы экспоненциального сглаживания, что позволяет учесть возможное будущее изменение экономических тенденций, на основе которых построена трендовая модель. Сущность данной поправки заключается в том, что она нивелирует недостаток адаптивных моделей, а именно, позволяет быстро учесть наметившиеся новые экономические тенденции. Fпр t = a Fф t-1 + (1-а) Fм t где: Fпр t - прогнозное значение объёма продаж; Fф t-1 – фактическое значение объёма продаж в предыдущем году; Fм t- значение модели; а –константа сглаживания Практическая реализация данного метода выявила следующие его особенности: для составления прогноза необходимо точно знать величину сезона. Исследования показывают, что множество продуктов имеют сезонный характер, величина сезона при этом может быть различной и колебаться от одной недели до десяти лет и более; применение полиномиального тренда вместо линейного позволяет значительно сократить ошибку модели; при наличии достаточного количества данных метод даёт хорошую аппроксимацию и может быть эффективно использован при прогнозировании объема продаж в инвестиционном проектировании. 20. Адаптивные методы прогнозирования ППП Statistica. Адаптивные методы используются в условиях сильной колеблемости уровней динамического ряда и позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда. К адаптивным методам относят: - методы скользящих и экспоненциальных средних, - метод гармонических весов, - методы авторегрессионных преобразований. Адаптивный метод относится к краткосрочному прогнозированию. Методы прогнозирования - экстраполяция тренда, регрессионно - корреляционный метод не всегда применимы. Тренд, регрессия описывают экономические процессы в среднем. Существуют такие нестационарные экономические процессы, математическое ожидание изменяется или экономический процесс описывается короткими динамическими рядами. Для увеличения надежности прогноза экономического развития в быстроизменяющихся условиях неполной информации возможно применение адаптивных моделей. Эти модели отражают текущие свойства динамического ряда и способны непрерывно учитывать эволюцию динамических характеристик, изучаемых процессов. Эти методы базируются на самокорреляционных моделях, которые учитывают результаты прогнозов, сделанных на предыдущем шаге. Модель постоянно впитывает новую информацию, приспосабливается к ней, поэтому отражает тенденцию развития, существующую в данный момент. Именно поэтому адаптивные модели особенно удачно используются при краткосрочном прогнозировании. Адаптивные методы позволяют учесть различную информационную ценность уровней временного ряда, а также степень устаревания данных. Начало адаптивному направлению в прогнозировании положила модель экспоненциального сглаживания. Например: Дан динамический ряд показателей хt.Модель можно записать следующим образом:  (5.13) (5.13)A, B – параметры модели, A оценивает информацию настоящего, B – прошлого. 0–A<1; А+В=1  . (5.14) . (5.14)Новый прогноз получается в результате корректировки предыдущего на 1 шаг. Для увеличения веса свежих наблюдений необходимо увеличить параметр адаптации А. Для сглаживания случайных отклонений уровней заданного динамического ряда параметр А необходимо снижать. Если эти 2 требования противоречат друг к другу, значит модель нуждается в оптимизации. Достигается это подбором параметра адаптации А: А=0,3 – принимают во всех случаях, но это оспаривается, для каждой модели параметр должен быть свой.  (5.15) (5.15)Каждый параметр адаптации А дает свою стандартную ошибку S. График с увеличением А увеличится и ст. от А. 21. Модели стационарных и нестационарных временных рядов ППП Statistica. Стационарные временные ряды. Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени. Временной ряд yt (t=1, 2, …, n) называется строго стационарным, если совместное распределение вероятностей n наблюдений y1, y2,…, yn такое же, как и n наблюдений y1+τ, y2+τ,…, yn+τ при любых n, t, и τ. Таким образом, свойства строго стационарных рядов не зависят от момента времени t. Нестационарные временные ряды. Пусть имеется временной ряд yt = ρyt-1+ ξt. Предположим, что ошибки ξt независимы и одинаково распределены, т.е. образуют белый шум. Перейдем к разностным величинам: Δyt = λyt-1+ ξt, где Δyt = yt – yt-1, λ= ρ-1. Если ряд Δytявляется стационарным, то исходный нестационарный ряд ytназывается интегрируемым (или однородным). Нестационарный ряд ytназывается интегрируемым (однородным) k-го порядка, если после k-кратного перехода к приращениям dkyt = dk-1yt – dk-1yt-1, где d1yt = Δyt, получается стационарный ряд dkyt. Если при этом стационарный ряд dkyt корректно идентифицируется как АРСС(p,q), то нестационарный ряд yt обозначается как АРПСС(p,k,q). Это означает модель авторегрессии – проинтегрированной скользящей средней (другое обозначение - ARIMA(p,k,q)) порядков p, k, q, которая известна как модель Бокса-Дженкинса. Процедура подбора такой модели реализована во многих эконометрических пакетах. 22. Построение уравнения множественной регрессии в ППП Excel и ППП Statistica. 1. Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии y=a+bx. Порядок вычисления следующий: 1) введите исходные данные:
2) выделите область пустых ячеек 5´2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1´2 – для получения только оценок коэффициентов регрессии; 3) активизируйте Мастер функций любым из способов: а) в главном меню выберите Вставка/Функция; б) на панели инструментов Стандартная щелкните по кнопке Вставка функции; 4) в окне Категория выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните по кнопке ОК; 5) заполните аргументы функции следующим образом: Известные_значения_y – диапазон, содержащий данные результативного признака (С2:С13); Известные_значения_x – диапазон, содержащий данные факторов независимого признака (В2:В13); Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении: если Константа=1, то свободный член рассчитывается обычным образом, если Константа=0, то свободный член равен 0 (указать 1); Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет: Статистика=1 - дополнительная информация выводится, Статистика=0 - выводятся только оценки параметров уравнения (указать 1). Щелкните по кнопке ОК; 6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем – на комбинацию клавиш CTRL + SHIFT + ENTER. 23. Применение ППП Excel и ППП Statistica в регрессионном анализе. Регрессионный анализ в STATISTICAКогда вы выбираете команду Множественной регрессии с помощью меню Анализ, открывается стартовая панель модуля Множественная регрессия. Вы можете задать регрессионное уравнение щелчком мыши по кнопке Переменные во вкладке Быстрый стартовой панели модуля Множественная регрессия. В появившемся окне Выбора переменных выберите Pt_Poor в качестве зависимой переменной, а все остальные переменные набора данных - в качестве независимых. Во вкладке Дополнительно отметьте также опции Показывать описательные статистики, корр. матрицы. Теперь нажмите OK этого диалогового окна, после чего откроется диалоговое окно Просмотр описательных статистик. Здесь вы можете просмотреть средние и стандартные отклонения, корреляции и ковариации между переменными. Отметим, что это диалоговое окно доступно практически из всех последующих окон модуля Множественная регрессия, так что вы всегда сможете вернуться назад, чтобы посмотреть на описательные статистики определенных переменных. Регрессионный анализ в Excel Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП. Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения. 24. Оценивание параметров производственных функций с применением ППП Excel и ППП Statistica. Получение уравнения регрессии происходит в два этапа: подбор вида функции и вычисление параметров функции. Выбор функции, в большинстве случаев, производятся среди линейной, квадратичной, степенной и др. видов функций. К функции предъявляются следующие требования: она должна быть достаточно простой для использования ее в дальнейших вычислениях и график этой функции должен проходить вблизи экспериментальных точек так, чтобы сумма квадратов отклонений y-координаты всех экспериментальных точек от y-координат графика функции была ба минимальной (метод наименьших квадратов). Для количественной оценки точности построения уравнения регрессии предназначен коэффициент детерминации R2, равный квадрату коэффициента корреляции и указывающий, какой процент изменения функции у объясняется воздействием факторов хk. Чем его значение ближе к 1, тем уравнение точнее описывает исследуемую зависимость. 25. Применение ППП Excel и ППП Statistica в статистическом анализе и прогнозировании. Наборы файлов данных системы STATISTICA (расширение *.sta) можно рассматривать как “рабочие книги” файлов, поскольку они содержат и автоматически сохраняют информацию обо всех дополнительных файлах (например, графиках, отчетах и программах), которые используются с текущим набором данных. STATISTICA использует стандартный интерфейс электронных таблиц. Текущий файл данных всегда отображается в виде электронной таблицы. Данные организованы в виде наблюдений и переменных. Наблюдения можно рассматривать как эквивалент столбцов электронной таблицы. Каждое наблюдение состоит из набора значений переменной. Система состоит из ряда модулей, работающих независимо. Каждый модуль включает определенный класс процедур. Почти все процедуры являются интерактивными, т.е. для запуска обработки необходимо выбрать из меню переменные и ответить на ряд вопросов системы. Это очень удобно для начинающего пользователя, однако резко замедляет деятельность опытного и не позволяет эффективно повторять одну и ту же процедуру несколько раз. |
