Главная страница
Навигация по странице:

  • Признак 1 Признак 2 Вектор 1

  • Вектор 2 1 3 Вектор 3

  • Вектор 4 2 4 Вектор 5

  • Вектор 6 2 5 Вектор 7

  • Вектор 8 5 2 Вектор 9

  • Вектор 10 7 2 Вектор 11

  • Вектор 12 7 3 Вектор 13

  • Методические указания Алгоритм таксономии

    		•

    Задание 2. Занятие 2 Решение задачи обучения методом kближайших соседей


    Скачать 77.5 Kb.
    НазваниеЗанятие 2 Решение задачи обучения методом kближайших соседей
    Дата22.10.2022
    Размер77.5 Kb.
    Формат файлаdoc
    Имя файлаЗадание 2.doc
    ТипЗанятие
    #749100




    Распознавание образов

    Практическое занятие 2-3. Решение задачи обучения методом k-ближайших соседей


    Цель работы

    Запрограммировать алгоритм обучения методом «k-ближайших соседей».
    Порядок выполнения

    1. В рамках создаваемого приложения, разработать программный модуль, для решения задачи таксономии. Результатом работы алгоритма должен стать список таксонов, сформированных при данном значении R:
      При пороговом расстоянии R сформировано yy таксонов:
      - Таксон №1 включает       xx векторов: 1,2,3,5,6
      - Таксон №2 включает       xx векторов: 7,9,11,12,15



    2. Протестировать работу алгоритма на проверочном наборе векторов:
    Признак 1
    Признак 2

    Вектор 1
    2
    2

    Вектор 2
    1
    3

    Вектор 3
    2
    3

    Вектор 4
    2
    4

    Вектор 5
    3
    4

    Вектор 6
    2
    5

    Вектор 7
    6
    1

    Вектор 8
    5
    2

    Вектор 9
    6
    2

    Вектор 10
    7
    2

    Вектор 11
    5
    1

    Вектор 12
    7
    3

    Вектор 13
    5
    4

    Вектор 14
    5
    5




    где, при пороговом расстоянии R=1 выделяются 3 таксона:

    • таксон №1: векторы 1-6

    • таксон №2: векторы 7-12

    • таксон №3: векторы 12-14




    1. Ввести в программу анкетные данные.




    1. Выполнить нормировку данных и сформировать таксоны при различных пороговых расстояниях R. Найти R, при котором сформировались наиболее адекватные группировки векторов.




    1. Дать интерпретацию полученных таксонов.


    Методические указания
    Алгоритм таксономии

    1. Задается некоторое пороговое расстояние R.

    2. Выбирается один из векторов таксономируемого множества, например, первый из них, и включается в таксон.

    3. В таксономируемом множестве ищутся векторы, удаленные от выбранного не больше, чем на R. Если таких векторов не обнаружено, формирование этого таксона заканчивается. Если такие векторы обнаружены, они включаются в таксон.

    4. Затем для каждого из вновь включенных в таксон векторов таким же образом ищутся ближайшие и тоже включаются в таксон и т. д. до тех пор, пока близкие векторы перестанут находиться. На этом формирования таксона заканчивается.

    5. Если остались векторы, не включенные в таксон, выбирается один из таких векторов, с которого начнется формирование нового таксона в соответствии с пунктами 3 и 4 и так до тех пор, пока все векторы не будут включены в таксоны.


    Количество таксонов, получаемых в результате работы алгоритма, зависит от величины R. При очень малых значениях R каждый таксон будет состоять из одного объекта, при слишком больших R все объекты могут объединиться в один таксон. Следующий рисунок иллюстрирует работу алгоритма для некоторого заданного R.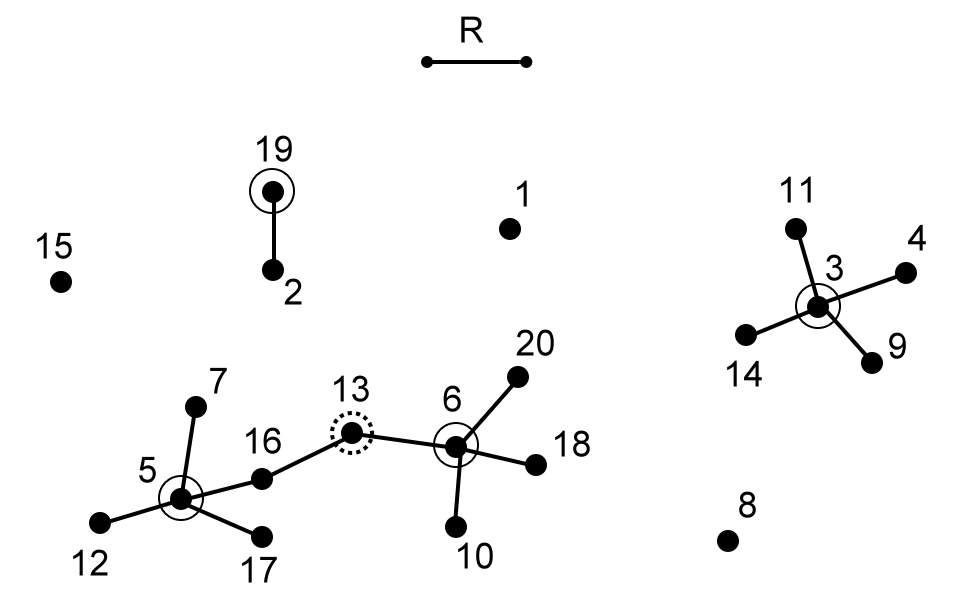



    Для вычисления расстояния между векторами используют метрику Евклида. При этом, если для описания объектов используются n признаков, то расстояние R между двумя векторами и вычисляется следующим образом:

    .
    (3.13)

    Приведенная формула применяется для вычисления расстояния межу векторами, координатами которых являются произвольные вещественные числа. При работе с векторами, координаты которых представлены в двоичном виде, применяется метрика Хемминга:

    .
    (3.14)


    Реализация алгоритма:

    1) задаем пороговое расстояние r_porog = 1

    написать администратору сайта