1. Характеристика предприятия электрических сетей как объекта исследования
 Скачать 264.41 Kb.
|
|
Поясним на примере обозначенную выше взаимосвязь между потерями мощности и значениями напряжения в узлах, реактивной мощности источников и коэффициентов трансформации. Рассмотрим фрагмент сети, схема замещения которого в общем случае содержит следующие комплексные параметры (рис. 2): продольное сопротивление  (проводимость  ) с нагрузочными потерями при протекании тока нагрузки  по линиям и трансформаторам и поперечную проводимость (шунт проводимости)  , отражающую преимущественно потери холостого хода трансформаторов, компенсирующих устройств и линий. В схеме замещения учтен идеальный трансформатор с действительным оэффициентом трансформации  ( ), поскольку в данных сетях производится только продольное регулирование напряжения и перераспределение реактивной мощности. Комплексные значения напряжения в начале участка  и в его конце  , различается падением напряжения  и объединенные трансформацией в виде ,определяются из расчетов исходного и оптимального режимов. В электрических сетях 35-110 кВ потери напряжения в основном определяются продольной составляющей падения напряжения  ,величина которой, а следовательно и значения напряжений в узлах в силу соотношения 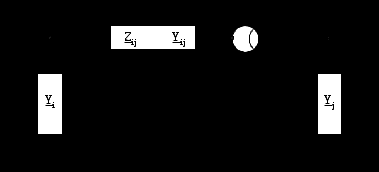 преимущественно определяется потоками реактивной мощности. Рисунок 2 – Общий фрагмент схемы замещения электрической сети Взаимосвязь параметров данной оптимизационной задачи можно представить с помощью известных формул. Потери активной мощности  ,  ,зависят от величины тока в продольной части схемы замещения (рис. 2)  ,и в ее поперечной части  .Анализируемые потери мощности выразим через модули напряжений и потери напряжения: в продольной части схемы замещения в виде  ,или иначе  ,а также в виде  ;в поперечной части  ,  .Отметим также зависимость потоков активной и реактивной мощностей  , ,и зарядной (емкостной) мощности шунтов  ,  ,от оптимизируемых значений напряжений и трансформаций. В итоге для электрической сети с n узлами суммарные потери мощности предстают в виде  ,Точное суммирование (интегрирование) потерь мощности в сети с m – ветвями и n – узлами при неизменном в период времени  составе и схеме позволяет определить суммарные потери электроэнергии в виде .Из выражений (2.22) следует, что для снижения нагрузочных потерь необходимо увеличить напряжение в узлах сети и в целом уровень (среднее значение) напряжения в ней. В то же время для снижения потерь холостого хода (2.23) уровень напряжения необходимо снижать. Воздействовать на напряжения и нагрузочные потери согласно выражениям (2.15), (2.16), (2.17) можно также путем снижения реактивных нагрузок продольных элементов сети, что достигается компенсацией реактивных нагрузок потребителей либо более благоприятным перераспределением перетоков  реактивной мощности в ветвях замкнутой сети /4, 7, 8/. Оба указанных мероприятия могут быть реализованы в ПЭС с помощью местных источников реактивной мощности, регулируемых трансформаторов в замкнутых контурах и оптимальным размыканием контуров. Поскольку потери мощности зависят от режима напряжений (2.20) - (2.23), а последний тесно связан с распределением реактивной мощности и трансформациями в сетях (2.15), (2.26), (2.27), понятие регулирования напряжения, реактивной мощности и коэффициентов трансформации объединяют, а соответствующую задачу решают совместно /9, 10/.Таким образом анализ составляющих потерь (2.20), (2.21), (2.22) в составе выражения их суммарных значений (2.26), (2.27), показывает, что экономичность режимов работы сетей в значительной мере зависит от сочетания коэффициентов трансформации и реактивных мощностей источников, влияющих на напряжения узлов, правильный выбор которых позволяет улучшить режим напряжений узлов и снизить потери мощности и энергии. В итоге возникает оптимизационная задача определения таких взаимосвязанных напряжений, коэффициентов трансформации и реактивных мощностей источников, при реализации которых суммарные потери активной мощности или электроэнергии сети (2.26) будут минимальны. При этом задача оптимизации режимов ЭС, относится к классической задаче нелинейного математического программирования, в общем случае имеет следующую формулировку /11, 12/: для (n+1) узлов ЭЭС найти минимум целевой функции  ,соответствующей функции суммарных потерь активной мощности (2.26) или ЭЭ (2.27) при условии баланса мощностей в узлах  ,  ,  ; , ,  ,  ;и при выполнении эксплуатационных и технических ограничений в виде неравенств  ,  ; , ; ,  .Предусмотрено разделение переменных  на зависимые (базисные)  и независимые (регулируемые)  переменные.Ограничения в виде равенств (2.29), (2.30) накладываются на активные и реактивные мощности в узлах потребления (нагрузки)  и активные мощности в узлах генерации  . Простые режимные ограничения (2.31) - (2.33), удерживающие оптимизируемые переменные в допустимых пределах, накладываются на реактивные мощности источников , напряжения во всех  пунктах сети и коэффициенты трансформации в  регулируемых трансформаторах.В общем случае балансовые ограничения (2.29), (2.30) контролируются на каждом шаге оптимизации с помощью уравнений установившихся режимов, нарушение простых ограничений (2.31) - (2.33) – добавкой к целевой функции (2.28) штрафной составляющей или (и) фиксацией переменных на нарушенных граничных значениях, сопровождаемых сменой состава зависимых и независимых переменных (смена базиса). Так при нарушении ограничений (2.31), реактивная мощность источников закрепляется на нарушенных пределах с увеличением на величину  количества ограничений (2.30). Выход за пределы напряжения в  м генераторном узле учитывается заменой (добавкой) соответствующего уравнения в системе (2.30) уравнением вида ,  .При этом на каждом шаге оптимизации производится анализ возможности снятия переменных с предела, соответственно корректируя количество  балансовых уравнений (2.29).Постановка и решение оптимизационной задачи возможны только при ненулевой степени ее свободы  ,наибольшая величина которой проявляется при отсутствии закрепленных на предельных значениях реактивной мощности или напряжений источников (  ) и коэффициентов трансформации регулируемых трансформаторов ( ) и равна количеству независимых переменных ( + ).Фиксация независимых оптимизируемых переменных во всех узлах генерации (  или  ,  ) на соответствующих пределах сводит задачу оптимизации (2.28) - (2.33) к решению 2 -мерной системы нелинейных УУР (2.29), (2.30).Методика решения предусматривает на каждом шаге оптимизации: а) расчет установившегося режима при заданных значениях регулируемых параметров и определение значения целевой функции; б) выполнение шага оптимизации, на котором происходит изменение регулируемых (независимых) параметров; в) сопоставление целевой функции с предыдущим значением. Решение данной оптимизационной задачи выполняется, как правило, на основе градиентных методов в детерминированной или стохастической постановках /11, 12/. 2.4 Описание метода оптимизации Целевую функцию оптимизации (2.28) можно записать подробно в виде  ,где  - нарушение ограничения (2.32), определяемое из выражения = , если  ; =0, если ; = , если  ;где  - штрафной коэффициент, подбирается эмпирически.Для определения наилучших напряжений источников, генераций реактивной мощности из источников и коэффициентов трансформации организуется итерационный процесс на каждой стадии которого определяется: Допустимое направление максимального уменьшения целевой функции (2.36)  ,где  - весовой коэффициент, учитывающий различные физические единицы  и  ;2 Направление изменения зависимых переменных (  ), необходимое для соблюдения баланса мощностей при изменении независимых переменных в направлении  ;3 Из условий ненарушения (2.31) - (2.33) и (2.37) - (2.39) находится максимальный допустимый шаг  в направлении  ;4 Вычисляются значения функции |