Лекции по информатике2. 1. информационная мера шеннона. Количество информации и избыточность
 Скачать 269.5 Kb.
|
1.ИНФОРМАЦИОННАЯ МЕРА ШЕННОНА.1.1.Количество информации и избыточность.Дискретные системы связи - системы, в которых как реализации сообщения, так и реализации сигнала представляют собой последовательности символов алфавита, содержащего конечное число элементарных символов. Пусть и - случайные величины с множествами возможных значений Х={х1,х2,...,хN}, Y={y1,y2,...,yM} Количество информации H() при наблюдении случайной величины X = {x1,x2,…,xN} с распределением вероятностей P={p1,p2,…рN}задается формулой Шеннона:  .Единицей измерения количества информации является бит, который представляет собой количество информации, получаемое при наблюдении случайной величины, имеющей два равновероятных значения. При равномерном распределении р1=р2=…=pN количество информации задается формулой Хартли:  Справедливы следующие соотношения: 0 H()log2N; N=2, p1=p2=0.5, H()=1; H(,)=H()+H(), если и -независимы. Избыточностью называется р= 1‑H(,)/max{ H() } = 1 ‑ H()/log2N. 1.2.Пример.Источник сообщений выдает символы из алфавита А={аi}, i = 1..4 с вероятностями р1 = 0.2, р2 = 0.3; р3= 0.4; р4= 0.1. Найти количество информации и избыточность. Решение. По формуле Шеннона Н(А)= -0.2 log20.2 – 0.3 log2 0.3 – 0.4 Iog2 0.4 – 0.1 log2 0.1 = 1.86 (бит). По определению избыточности р = 1 – H(A)! log2 4 = 0,07. 1.3.ЗадачиЗадача 1. Определить энтропию и избыточность источника информации А, передающего сообщения Аi, i= 1..4. Вероятность сообщений определяются по формулам: р1= 0.2 + 0.005.V; р2= 0.3 ‑ 0.005.V; р3= 0.1 + 0.01.V; р4= 0.4 ‑ 0.01.V, где V – номер варианта. Задача 2. На выходе источника сообщений может появляться нуль и единица. Вероятность появления каждого сообщения изменяется со временем и в каждый момент времени может быть определена по формулам: p(1) = 0.9 – 0.02.(V - 1) – 0.1.t, p(0) = 0.1 + 0.02.(V - 1) + 0.1.t, Необходимо исследовать изменение энтропии источника информации во времени и определить момент времени, когда математическая модель опыта теряет смысл. Энтропия источника сообщений вычисляется в соответствии с формулой Шеннона. Все вычисления сводятся в табл.2: Таблица 2
Значения t задаются целыми числами через равные промежутки времени t = 0,1,2,... Математическая модель опыта имеет смысл, когда выполняются соотношения для вероятностей р(1)+р(0)= 1; 0 р(0) 1; 0 р(1) 1. Значения t, при котором эти соотношения перестают выполняться, и есть момент времени, когда модель опыта теряет смысл. После заполнения таблицы результатами вычислений следует построить графики изменения H(0), H(1), H. При анализе графиков обратить внимание на точку, где энтропия принимает наибольшее значение и наименьшее значение. Указать значения вероятностей появления символов в этих точках и моменты времени. 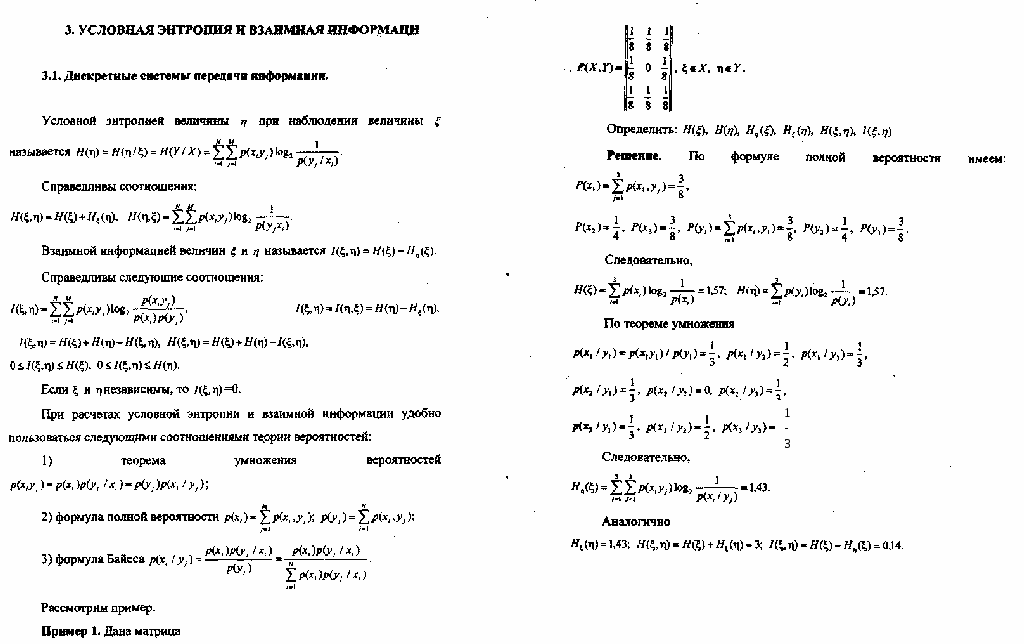 Задача 1 Сигнал подается на вход канала (величина ) с вероятностью  (логическая единица) и отсутствует (логический ноль) с вероятностью (1 – р). Вероятность того, что поступившая единица правильно воспроизведена на выходе – p.0.8, а вероятность правильного воспроизведения нуля – p.0.95 (величина ). Найти энтропию выхода, энтропию входа, взаимную информацию входа и выхода I(S,S');Задача 2 Распределение вероятностей входных и выходных сигналов системы заданы следующей матрицей: 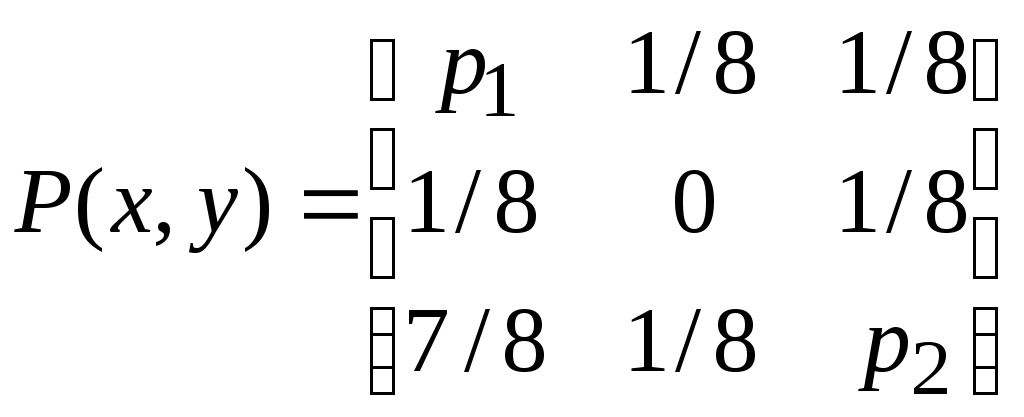 , где  Определить энтропию входа H(Y ), условную энтропию H(Y/X)и Н(Х/Y ), взаимную информацию I (X,Y ). ХАРАКТЕРИСТИКИ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ Каналы передачи информации Канал связи представляет собой совокупность технических средств для передачи сообщений из одной точки пространства в другую. С точки зрения теории информации физическое устройство канала несущественно. Источник сообщений (ИС) имеет выходной алфавит символов A={аi}, i=1..n - количество информации, приходящееся в среднем на один символ источника:  где pi, - вероятность появления символа ai, на выходе источника, символы источника считаются независимыми. Канал связи имеет алфавит символов B={bj}, j=1..m, среднее количество информации в одном символе канала  где qj - вероятность появления символа bi, в канале. Техническими характеристиками канала связи являются: техническая производительность источника A - среднее число символов, выдаваемых источником в единицу времени; техническая пропускная способность канала связи B - среднее число символов, передаваемое по каналу в единицу времени. Информационной характеристикой источника является информационная производительность. По определению, информационная производительность - это среднее количество информации, выдаваемое источником в единицу времени.  В канале без помех информационными характеристиками являются: 1 ) скорость передачи информации по каналу  2) пропускная способность канала  где {P} - множество всех возможных распределений вероятностей символов алфавита В канала. С учетом свойств энтропии CK=B.log2m. В канале с помехами в общем случае входной и выходной алфавиты не совпадают. Пусть BВХ=X={x1,x2,…,xn}; BВЫХ=Y={y1,y2,…,ym}. Если отправленный на входе канал символ хкопознан в приемнике как yi и iK, то при передаче произошла ошибка. Свойства канала описываются матрицей переходных вероятностей (вероятность приема символа уi, при условии, что послан хk): || P(yi|xk) ||, k=1..n, i=1..m. Справедливо соотношение:  Среднее количество информации на один входной символ канала:  pi=p(xi).Среднее количество информации на выходной символ канала:  Информация, которую несет выход канала о входе:  I(Y,X)=H(X)-HY(X)=H(Y)-HX(Y).Здесь Ну(Х) - условная энтропия входного символа канала при наблюдении выходного символа (ненадежность канала), Нх(Y) - условная энтропия выходного символа канала при наблюдении входных символов (энтропия шума). Скорость передачи информации по каналу с помехами: dI(B)/dt=BI(X,Y). Пропускная способность канала с помехами: где { р} - множество всех возможных распределений вероятностей входного алфавита символов канала. Рассмотрим пример Н  айти пропускную способность двоичного симметричного канала (канала с двухсимвольными входными и выходными алфавитами) и одинаковыми вероятностями ошибок (рис.1), если априорные вероятности появления входных символов: P(x1)=P1=P, P(x2)=P2=1-P.Решение. В соответствии с моделью канала условные вероятности P(y1 | x2) = P(y2 | x1) = Pi, P(y1 | x1) = P(y2 | x2) = 1-Pi. Пропускная способность канала - CK=B.max{H(Y)-H(X|Y)}. Найдем энтропию шума:  По теореме умножения: P(yjxi)=P(xi)P(yj|xi), следовательно, P(x1y1)=P(1-Pi), P(x2y1)=(1-P)Pi, P(x1y2)=PPi, P(x2y2)=(1-P)(1-Pi). Подставляя в формулу, получаем:  Таким образом, H(Y|X) не зависит от распределения входного алфавита, следовательно:  Определим энтропию выхода:  Вероятности P(y1) и P(y2)получаем следующим образом: P(y1)=P(y1x1)+P(y1x2)=P(1-Pi)+(1-Pi)Pi,P(y2)=P(y2x1)+P(y2x2)=PPi+(1-P)(1-Pi). Варьируя Р, убеждаемся, что максимальное значение H(Y), равное 1, получается при равновероятных входных символах P(y1) и P(y2). Следовательно,  Задача. Найти пропускную способность канала с трехсимвольными входными и выходными алфавитами (x1, x2, x3 и y1, y2, y3 соответсвенно). Интенсивность появления символов на входе канала k=V.10 символов/с. Вероятности появления символов:  ,  ,  .Вероятности передачи символов через канал связи:  ,  ,  , ,  ,  , ,  ,  .4. КОДИРОВАНИЕ ИНФОРМАЦИИ 4.1. Общие сведения Кодом называется: - правило, описывающее отображение одного набора знаков в другой набор знаков или в набор слов без знаков; - множество образов, получающихся при таком отображении. В технических кодах буквы, цифры и другие знаки почти всегда кодируются двоичными последовательностями, называемыми двоичными кодовыми словами. У многих кодов слова имеют одинаковую длину (равномерные коды). Выбор кодов для кодирования конкретных типов сообщений определяется многими факторами: - удобством получения исходных сообщений из источника; - быстротой передачи сообщений через канал связи; - объёмом памяти, необходимым дня хранения сообщений; - удобством обработки данных; - удобством декодирования сообщений приемником. Закодированные сообщения передаются по каналам связи, хранятся в ЗУ, обрабатываются процессором. Объемы кодируемых данных велики, и поэтому во многих случаях важно обеспечить таксе кодирование данны:'., которое характеризуется минимальной длиной получающихся сообщений, Это проблема сжатия данных. Существуют два подхода сжатия данных: - сжатие, основанное на анализе статистических свойств кодируемых сообщений. Сжатие на основе статистических свойств данных называется так же теорией экономного или эффективного кодирования. Экономное кодирование основано на использовании кодов с переменной длиной кодового слова, например, код Шеннона-Фано, код Хафмана /31. Идея использования кодов переменной длины для сжатия данных состоит в том, чтобы сообщения с большей вероятностью появления ставить в соответствие кодовые комбинации меньшей длины и, наоборот, сообщения с малой вероятностью появления кодировать словами большей длины. Средняя длина кодового слова определяется с.о.:  где /, - длина кодового слова для кодирования i - го сообщения; pt - вероятность появления i - го сообщения. 4.2. Задания 4.2.1. Из табл.4 выбрать дня последующего кодирования исходный алфавит, содержащий 10 символов, начиная с N-ro (N -порядковый номер студента в журнале группы). Пронормировать вероятности символов. 4.2.2. Пронормировать выбранный в п.4.2.1. исходный алфавит равномерным двоичным кодом, кодом Шеннона-Фано, кодом Хафмана. Для каждого варианта кодирования рассчитать минимальное, максимальное, среднее значение длины кодового слова. Проанализировать результаты. 4.2.3. Проделать задание 4.2.2. для троичного кода. Таблица 4
4.3. Указания к выполнению отдельных заданий К заданию 4.2.1. Нормирование вероятностей производится по формуле: /W-HO / *Рк ' JC=AT где Pi - вероятности появления символов, приведенные в табл.4. К заданию 4.2.2. Правила построения двоичных кодов изложены в /4,6/. К заданию 4.2.3. При построении троичного кода в качестве кодовых слов берутся слова, записанные в троичной системе счисления. Оптимальный троичный код строится с помощью процедуры Хафмана (с помощью процедуры Шеннона-Фано строится субоп-тимальный код). При этом разбиение алфавита ведется на три группы, первой группе приписывается "О", второй - "1", третьей - "2". ПРИЛОЖЕНИЕ 1 ЗНАЧЕНИЕ ФУНКЦИИ –P. log2( P) Таблица
ПРИЛОЖЕНИЕ 2 ЗНАЧЕНИЕ ФУНКЦИИ log2( 1/P) Таблица
|