1. Исследование функции на безусловный экстремум 3
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
2. Численные методы безусловной минимизацииЧисленное решение задачи минимизации (1), как правило, связано с построением минимизирующей последовательности точек x0,x1,x2,…,xn,…, обладающих свойством f(xk)<f(xk-1), k=0,1,… (3) Общее правило построения минимизирующей последовательности имеет вид xk+1=xk+tkdk, k=0,1,...., где х0 начальная точка поиска, dk приемлемое направление перехода из точки xk в точку xk+1, которое обеспечивает выполнение условий (3) и называется направлением спуска, tk величина шага. Начальная точка поиска задается, исходя из физического содержания решаемой задачи и априорных данных о наличии и положении точек экстремума. При решении вопроса о выборе численного метода рекомендуется оценить поведение линий уровня целевой функции в окрестностях предполагаемой точки экстремума. Число m = L/l, где L - максимальное, а l-минимальное собственные значения гессиана функции f в предполагаемой точке экстремума x0(характеризующее, вообще говоря, разброс собственных значений оператора f (x)) называют числом обусловленности гессиана функции f в точке x0. Если m >> 1, то функцию называют плохо обусловленной или овражной. “Овражность”, то есть вытянутость линий уровня вдоль одного направления, приводит к тому, что градиентные методы сходятся медленно. В зависимости от наивысшего порядка частных производных функции f(x), используемых для формирования dk и tk, численные методы принято делить на три группы:
Метод конфигураций (Хука-Дживса)Состоит из двух этапов: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. Направления поиска – координатные направления. По каждому направлению поочередно с шагом +t0 (-t0), проверяется выполнение условия (2), и в качестве нового базиса берется точка, с координатами, полученными в результате удачных шагов из начальной точки по каждому направлению. Направление от старого базиса к новому задает направление ускорения поиска: в качестве следующей точки минимизирующей последовательности проверяется точка y1=x0+(x1-x0). Здесь - ускоряющий множитель, задаваемый пользователем. Если полученная точка является удачной, то она берется в качестве следующей точки для исследования. В противном случае исследование ведется из точки x1. Метод деформируемого многогранника (Нелдера-Мида)Строится последовательность множеств из n+1 точек, которые являются вершинами выпуклого многогранника. На каждом последующем k+1-м шаге из системы точек xi(k), i=1, … ,n+1, выводится точка xh(k), в которой функция f(x) имеет наибольшее значение (худшая точка). Вместо точки xh(k) в систему вводится новая точка, выбираемая на отрезке прямой, проходящей через худшую точку и центр тяжести оставшихся nвершин многогранника: xn+2= 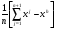 - центр тяжести; - центр тяжести;xn+3= xn+2+( xn+2- xh) – новая точка (“растянутое” отражение наихудшей вершины). Метод дробления шагаСтроится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности{xk} вычисляются по правилу xk+1=xk-tkgrad f(xk), k=0,1,.... (4) Точка х0 задается пользователем; grad f(xk) – градиент минимизируемой функции, вычисленный в точке xk; величина шага t0 задается пользователем и остается постоянной до тех пор, пока функция убывает в точках последовательности, что контролируется путем проверки выполнения условия f(xk+1)-f(xk) <0 (или <-ε). Если условие убывания не выполняется, величина шага уменьшается, как правило, вдвое, то есть, tk=tk/2. Метод наискорейшего градиентного спускаСтроится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности {xk} вычисляются по правилу xk+1=xk-tkgrad f(xk), k=0,1,... . Точка х0 задается пользователем; gradf(xk) – градиент минимизируемой функции, вычисленный в точке xk; величина шага tk определяется из условия минимума функции φ(tk)=а(xk-tkgradf(xk)). Задача минимизации одномерной функции φ(tk) может быть решена с использованием необходимого условия минимума 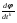 =0 с последующей проверкой достаточного условия минимума =0 с последующей проверкой достаточного условия минимума 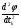 >0 или с использованием численных методов. >0 или с использованием численных методов.Метод сопряженных направлений (Флетчера – Ривса)Строится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности{xk} вычисляются по правилу: xk+1=xk-tkdk, k=0,1,....; dk=- grad f(xk)+βk-1dk-1; (4) d0=- grad f(x0); βk-1=║ grad f(xk)║2∕║ grad f(xk-1)║2 Точка х0 задается пользователем; величина шага tk определяется из условия минимума функции φ(t)=а(xk-tdk)). Задача минимизации одномерной функции φ(tk) может быть решена с использованием необходимого условия минимума (dφ/dt)=0 с последующей проверкой достаточного условия минимума 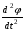 >0 или с использованием численных методов. >0 или с использованием численных методов.Метод НьютонаСтроится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности{xk} вычисляются по правилу xk+1=xk+dk, k=0,1,..... Точка х0 задается пользователем с учетом знакопостоянства и невырожденности матрицы Гессе в задаваемой начальной точке и близости выбранной точки к предполагаемой точке минимума. Направление спуска определяется для каждого значения k по формуле dk=-H-1(xk)gradf(xk), где Н – матрица Гессе. Порядок выполнения лабораторной работы
Пример выполнения лабораторной работыФункция: 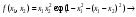 min, x0=(-2,-2). min, x0=(-2,-2). Методы: градиентного спуска и Ньютона. Решение. Примечание: при построении графика используется среда MathCAD 12.1. 1. Построим график функции и линии уровня. 2. Решим задачу минимизации аналитически. 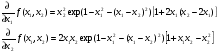 Система для нахождения стационарных точек из условия равенства нулю градиента имеет вид 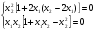 Если x1x2 =0 тоиз системы следует, что x1 =0 иx2 =0 Первая стационарная точка – A0(0;0). Если x1x2 ≠0: 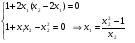 Подставим х1 в первое уравнение: 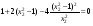 Введем замену 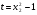 : :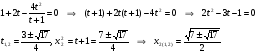 Обозначим 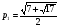 , , 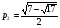 . .Получаем остальные стационарные точки: 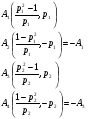 Приближенные числовые координаты найденных точек: А0(0;0), А1(1.068;1.668), А2(-1.068;-1.668), А3(-0.331;0.848), А4(0.331;-0.848). Построим и исследуем на знакоопределенность матрицу Гессе в точках А0,…,А4. 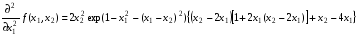 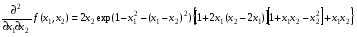 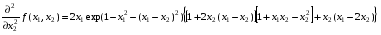 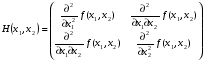 H(A0(0;0))=0 (требуется дополнительное исследование точки). Анализ поведения функции в окрестности точки A0(0;0) показывает, что, придавая х1 положительное и отрицательное значение при любом х2, можно получить соответственно положительное и отрицательное значение функции. Таким образом, A0(0;0) не является ни точкой локального минимума, ни точкой локального максимума. Н(А1(1.068;1.668))≈ 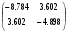 , отрицательно определена, в точке локальный максимум. , отрицательно определена, в точке локальный максимум.Н(А2(-1.068;-1.668))≈ 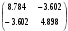 , положительно определена, в точке локальный минимум. , положительно определена, в точке локальный минимум.Н(А3(-0.331;0.848))≈ 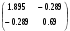 , положительно определена, в точке локальный минимум. , положительно определена, в точке локальный минимум.Н(А4(0.331;-0.848)) ≈ 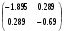 , отрицательно определена, в точке локальный максимум. , отрицательно определена, в точке локальный максимум.Точками глобального экстремума являются А1(1.068;1.668) – глобальный максимум, f (A1) ≈1.801; А2(-1.068;-1.668)– глобальный минимум, f (A2) ≈-1.801. 3. Остальные задания реализованы на языке СИ, для чего написаны классы для работы с векторами и матрицами (CVector и CMatrix) и использующее их приложение. В методе наискорейшего спуска для одномерной минимизации используется метод золотого сечения. Для отыскания собственных чисел матрицы Гессе применяется метод Якоби, для построения обратной матрицы – метод Жордана-Гаусса. В начале работы программа выводит информацию о стационарных точках: Stationary dots: x1 x2 f(x1,x2) Extreme 1.067890 1.667566 1.801131 LOC MAX -1.067890 -1.667566 -1.801131 LOC MIN -0.331077 0.848071 -0.144426 LOC MIN 0.331077 -0.848071 0.144426 LOC MAX GLOBAL MIN: x(-1.067890, -1.667566) f(x) = -1.801131 GLOBAL MAX: x(1.067890, 1.667566) f(x) = 1.801131 Затем устанавливается начальная точка x0(-2,-2), функция исследуется на выпуклость/вогнутость в этой точке, выводится число обусловленности матрицы Гессе: x0(-2.000000, -2.000000) Hessian: Alternating sign f(x0) = -0.398297 cond H(x0) = 4.751665 Таким образом, квадратичная форма, соответствующая матрице Н(-2,-2), является знакопеременной. Функция не является “овражной” в окрестности точки, и допустимо применение метода градиентного спуска. Далее запускается метод наискорейшего градиентного спуска, и выполняются 2 итерации. Steepest descent method: x2(-1.200031, -1.706888) Hessian: Convex grad_f(x2) = (-0.963083, 0.275166) f(x2) = -1.741440 В результате 2 итераций мы получили точку, достаточно близкую к точке глобального минимума. Теперь из точки 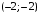 стартует метод Ньютона с поправкой гессиана. Результат двух итераций: стартует метод Ньютона с поправкой гессиана. Результат двух итераций:Newton method: x2(-2.735431, -2.306328) Hessian: Alternating sign grad_f(x2) = (-0.110421, 0.031948) f(x2) = -0.018516 Видно, что метод расходится. Начальная точка выбрана неудачно; увеличение числа итераций приводит к дальнейшему расхождению метода. Это объясняется тем, что метод Ньютона применим в окрестности точки минимума. Анализируя линии уровня функции, выберем начальную точку ближе к оптимальной. Например, 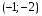 : :x0(-1.000000, -2.000000) Hessian: Convex f(x0) = -1.471518 cond H(x0) = 3.786885 Newton method: x2(-1.047041, -1.722604) Hessian: Convex grad_f(x2) = (0.379214, -0.339841) f(x2) = -1.787758 Как в начальной, так и в конечной точке функция является выпуклой. За две итерации мы приблизились к точке 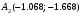 . .Теперь возьмем начальную точку еще ближе к 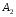 , например , например 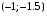 : :x0(-1.000000, -1.500000) Hessian: Convex f(x0) = -1.752302 cond H(x0) = 3.857905 Newton method: x2(-1.067889, -1.667566) Hessian: Convex grad_f(x2) = (0.000000, 0.000000) f(x2) = -1.801131 Метод Ньютона достиг точки глобального минимума, об этом говорит практически нулевой вектор-градиент. Точное значение 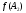 отличается от найденного отличается от найденного 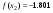 на 4.729∙10-7(по модулю). на 4.729∙10-7(по модулю).Выводы В лабораторной работе проведено исследование заданной функции на глобальный экстремум с использованием аналитических преобразований, графика функции и разработанного приложения на языке C++. С помощью метода градиентного спуска удалось улучшить целевую функцию без каких-либо дополнительных действий. Метод Ньютона при выборе в качестве начальной точки x0(-2,-2) не сошелся. Проблема была решена заменой начальной точки на более подходящую для данного метода. Это позволило за две итерации прийти в точку глобального минимума. Полученные результаты хорошо согласуются с теорией. Разработанные классы CVector и CMatrix могут применяться в будущих проектах. |
