1. Исследование функции на безусловный экстремум 3
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
3. Решение задачи минимизации со смешанными ограничениямиОбщая задача нахождения экстремума функции при наличии ограничений - равенств и ограничений - неравенств записывается в следующем виде: f(x)→ extr, (5) xX= {xEn: gi(x)≤0, i=1,2,...,r; gi(x)=0, i=r+1, ..., m, m-r где среди функций f(x) и gi(x) могут быть нелинейные. Активные ограничения – неравенства в точке х* ─ это ограничения, которые выполняются в данной точке в виде равенства. Пассивные ограничения – неравенства в точке х* ─ это ограничения, которые выполняются в данной точке в виде строгого неравенства. Если градиенты активных ограничений-неравенств и ограничений-равенств в точке х* линейно независимы, то говорят, что в оптимальной точке выполнено условие регулярности. Обобщенная функция Лагранжа для задачи со смешанными ограничениями задается как L(x,λ0,λ)=λ0f(x)+ 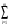 λigi(x) (6) λigi(x) (6)В случае регулярности 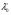 ≠0, и можно положить этот коэффициент равным 1. ≠0, и можно положить этот коэффициент равным 1.Теорема Куна – Таккера (дифференциальная форма необходимого условия минимума) Пусть точка х* - точка локального минимума в задаче математического программирования (5), функцииf,gr+1,...,gm дважды непрерывно дифференцируемы в точке х, функции g1,...,gr дважды непрерывно дифференцируемы в некоторой окрестности точки x. Тогда существует число 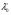 и вектор и вектор 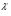 такие, что выполняются следующие условия: такие, что выполняются следующие условия:
gradxL(x*, 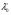 , ,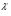 )=0 )=0
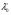 2+ 2+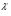 2>0 2>0то есть, хотя бы один из множителей Лагранжа отличен от нуля;
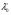 ≥0, ≥0, 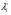 ≥0, i=1, ..., r, ≥0, i=1, ..., r,то есть, множители Лагранжа, соответствующие целевой функции и ограничениям – неравенствам, неотрицательны;
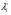 gi(x*)=0, i=1, 2, ..., r gi(x*)=0, i=1, 2, ..., rЕсли при этом выполнено условие регулярности, то справедливо следующее Утверждение: Если функции f, gr+1,..., gm выпуклые, а функции g1,..., gr – линейные, то условия теоремы Куна – Таккера являются одновременно и достаточными условиями глобального минимума. Достаточное условие минимума первого порядка: Пусть имеется точка (х*, 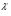 ), удовлетворяющая условию стационарности обобщенной функции Лагранжа по х при ), удовлетворяющая условию стационарности обобщенной функции Лагранжа по х при  ≠0, суммарное число активных ограничений-неравенств в точке х* и ограничений-равенств совпадает с числом переменных n. Если ≠0, суммарное число активных ограничений-неравенств в точке х* и ограничений-равенств совпадает с числом переменных n. Если 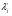 >0 для всех активных ограничений gj(x), то точка х* - точка условного локального минимума в задаче (5). >0 для всех активных ограничений gj(x), то точка х* - точка условного локального минимума в задаче (5).Достаточное условие минимума второго порядка: Пусть имеется точка (х*, 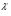 ), удовлетворяющая условию стационарности обобщенной функции Лагранжа по х при ), удовлетворяющая условию стационарности обобщенной функции Лагранжа по х при  ≠0. Если в этой точке d2L(х*, ≠0. Если в этой точке d2L(х*,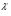 )>0 для всех ненулевых dx таких, что для активных в точке х* ограничений-неравенств dgj(x*)=0, )>0 для всех ненулевых dx таких, что для активных в точке х* ограничений-неравенств dgj(x*)=0, 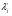 >0 и dgj(x*)≤0, >0 и dgj(x*)≤0, 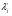 =0, то точка х* является точкой локального минимума. =0, то точка х* является точкой локального минимума.Общая схема решения задачи условной минимизации функции:
Седловые точки функции ЛагранжаСуществование экстремума тесно связано с наличием у функции Лагранжа (6) так называемой седловой точки. Рассматривается задача выпуклого программирования с ограничениями-неравенствами f(x)→ min, (7) xX= {xEn: gi(x)≤0, i=1,2,..., m; х≥0}, Предполагается, что выполнено условие регулярности, то есть, можно рассматривать только вариант λ 0=1. Определение Точка (х*, 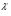 ), где х* Х, ), где х* Х, 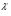 Еm, Еm, 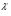 ≥0, называется седловой точкой функции Лагранжа L(x,λ), если ≥0, называется седловой точкой функции Лагранжа L(x,λ), если L(x*,λ)≤ L(x*, 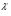 )≤ L(x, )≤ L(x, 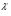 ) (8) ) (8)Утверждение 1 (критерий для седловых точек функции Лагранжа). Точка (х*, 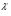 )– является седловой для функции Лагранжа L(x,λ) в том и только том случае, когда выполнены условия )– является седловой для функции Лагранжа L(x,λ) в том и только том случае, когда выполнены условияL(х*, 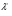 )=min {L(x, )=min {L(x, 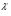 )׀ x Х}, (9) )׀ x Х}, (9)L(х*, 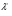 )=max {L (x*,λ)׀ λ ≥0}, (10) )=max {L (x*,λ)׀ λ ≥0}, (10)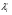 gi(x*)=0, i=1, 2, ..., m. (11) gi(x*)=0, i=1, 2, ..., m. (11)х*≥0 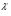 ≥0 ≥0Условие (9) минимума функции Лагранжа по х эквивалентно выполнению в точке (х*, 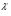 ) неравенства ) неравенства 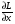 ≥0. (9′) ≥0. (9′)Условие (6) максимума функции Лагранжа по λ эквивалентно выполнению в точке (х*, 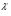 ) неравенства ) неравенства 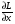 ≤0. (10′) ≤0. (10′)Утверждение 2. х* - оптимальное решение задачи (3) в том и только том случае, когда существует такой вектор 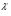 ≥0, что (х*, ≥0, что (х*,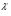 ) – седловая точка функции Лагранжа L (x,λ). ) – седловая точка функции Лагранжа L (x,λ).Метод седловой точки в задачах квадратичного программированияРассмотрим задачу квадратичного программирования, то есть, f(x)=(Сx,x) +(d,x) 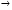 min (12) min (12)g(x)=Ax ≤ b, где С – матрица размера n*n, d,х – векторы-столбцы n*1, А – матрица размера m*n, b – вектор-столбец m*1. Для задачи квадратичного программирования критерий существования седловой точки приобретает вид задачи решения СЛАУ. Действительно: Функция Лагранжа в этом случае запишется в виде L = 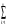 dkxk+ dkxk+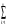 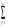 ckjxkxj+ ckjxkxj+ 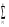 λi( λi(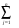 aijxj-bi), (13) aijxj-bi), (13)где ckj – элементы матрицы С, dk – элементы вектора d, bi – элементы вектора свободных членов b, aij – элементы матрицы А, λi – коэффициенты Лагранжа. Необходимые и достаточные условия оптимальности решения х* принимают вид vj  dj+2 dj+2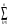 ckjxk+ ckjxk+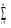 λiaij , vj≥0, (j=1,...,n) (14) λiaij , vj≥0, (j=1,...,n) (14)-yi  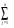 aijxj-bi , -yi≤0, (i=1,...,m) (15) aijxj-bi , -yi≤0, (i=1,...,m) (15)xjvj=0, xj≥0, (j=1,...,n) (16) λi(-yi)=0, λi≥0 (17) Равенства (14). (15) образуют систему n+m линейных уравнений с 2(n+m) неизвестными x1,...,xn,v1,...,vn, λ1,..., λm,y1,...,ym. Решения этой системы, при которых выполняются равенства (16), (17), дают координаты седловой точки (х*,λ*). Чувствительность решения ЗНП Пусть х*=х*(b) решение задачи нелинейного программирования f(x)→ min, (13) xX= {xEn: gi(x)≤bi, i=1,2,..., m; х≥0}, при некотором векторе b свободных членов в ограничениях – неравенствах, а v(b), соответственно, значение целевой функции при этом решении ЗНП, то есть, v(b)=f(x*). Тогда справедлива следующая оценка изменения целевой функции: ∆v=f(b+∆b)-f(b) при изменении вектора b на некоторый малый вектор-приращение ∆b: ∆f≈(∆b ,λ*), (14) где λ* - вектор множителей Лагранжа, соответствующий решению х*(b). Метод проекции градиента для задачи условной оптимизацииЗадача v=inf f(x), xUEn Метод xk+1 = PU (xk – αk df(xk)) Метод условного градиента для задачи условной оптимизацииЗадача v=inf f(x), xUEn Метод xk+1 = xk + αk (xk′ - xk), где xk′ - решение вспомогательной задачи inf (df(xk), xk′ - x), x U. 0< αk <=1, αk = +, lim αk = 0 Метод возможных направлений для задачи условной оптимизацииЗадача v=inf f(x), gi(x) ≤ 0, i = 1,…,m Метод xk+1 = xk + αk e, где e - решение вспомогательной задачи min σ, (df(xk), e) ≤ σ, (dgi(xk), e) ≤ σ, i I(xk) |e| ≤ 1 Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
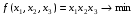 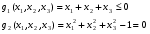 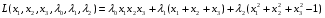 Допустимая область – часть сферы 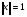 , лежащая в подпространстве , лежащая в подпространстве 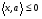 , , 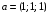 . .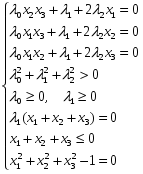 (1) (1)(2) (3) (4) (5) (6) (7) (8) Рассмотрим случай 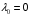 . .Если при этом 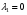 , то , то 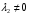 . .Из (1)…(3) 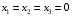 , что противоречит (8). , что противоречит (8).Если 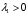 , то , то 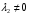 (иначе получаем противоречия в (1)…(3)). (иначе получаем противоречия в (1)…(3)).Из (1)…(3) 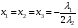 . Подставим в (6): . Подставим в (6):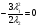 . Отсюда . Отсюда 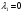 . Но . Но 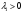 , пришли к противоречию. , пришли к противоречию.Рассмотрим теперь случай 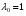 . .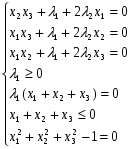 (1′) (1′)(2′) (3′) (4′) (5′) (6′) (7′) Если 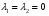 , то получаем точку , то получаем точку 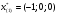 (из (1′)…(3′),(7′)). (из (1′)…(3′),(7′)).Остальные «симметричные» точки здесь и далее приводить не будем. Если 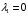 , , 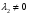 , , 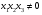 , то: , то:(1′),(2′) 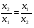 (2′),(3′) 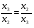 (7′) 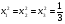 Из (6′) получаем точки 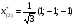 и и 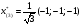 . . 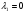 , , 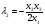 . Для . Для 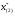 значение значение 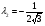 , для , для 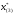 значение значение 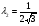 . .Если 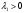 , , 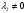 : :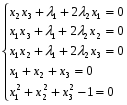 (1′′) (1′′)(2′′) (3′′) (4′′) (5′′) Если 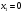 , то (2′′),(3′′) , то (2′′),(3′′) 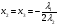 ; (4′′) ; (4′′) 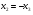 . .Следовательно, 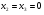 и и 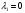 . Но . Но 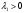 , пришли к противоречию. , пришли к противоречию.Значит, 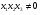 . .(1′′)+(2′′)+(3′′): 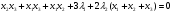 Последнее слагаемое равно нулю согласно (4′′). Поэтому, 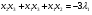 . .С другой стороны, 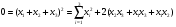 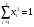 (по (5′′)) (по (5′′))Следовательно, 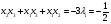 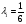 . .Если 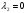 , то (1′′)…(3′′) , то (1′′)…(3′′) 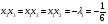 . .Разделим на 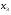 : : 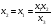 . Но если . Но если 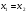 , то их произведение не может быть равно , то их произведение не может быть равно 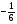 . Значит, . Значит, 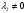 . .Если 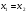 , получаем систему: , получаем систему: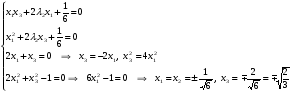 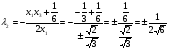 Получаем точку 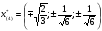 (в силу симметрии переменных (в силу симметрии переменных 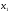 , , 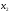 , , 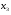 координаты можно переставить), координаты можно переставить), 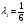 , , 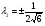 . .Предположив 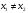 , получим те же результаты. , получим те же результаты.Найдены следующие точки: 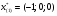 , , 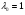 , , 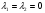 ; ;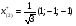 , , 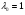 , , 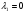 , , 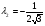 ; ;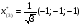 , , 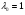 , , 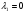 , , 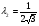 ; ;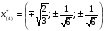 , , 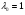 , , 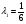 , , 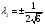 . .Запишем второй дифференциал обобщенной функции Лагранжа. 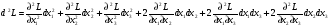 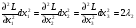 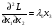 , , 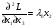 , , 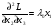 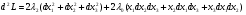 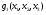 является активным ограничением только для точки является активным ограничением только для точки 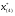 . .Применим достаточное условие минимума второго порядка к этой точке: 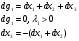 Подставив 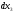 и и 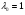 во второй дифференциал функции Лагранжа, получим: во второй дифференциал функции Лагранжа, получим: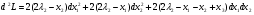 Запишем матрицу квадратичной формы относительно приращений: 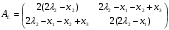 Для «верхнего» знака 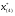 матрица матрица 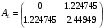 . Для «нижнего» знака элементы матрицы меняют знак. Согласно критерию Сильвестра, в этой точке нет экстремума. . Для «нижнего» знака элементы матрицы меняют знак. Согласно критерию Сильвестра, в этой точке нет экстремума.Сравним значения функции в остальных точках: 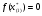 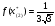 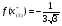 Точкой глобального минимума является 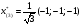 , значение функции в этой точке , значение функции в этой точке 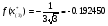 . . 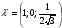 Проверим справедливость оценки 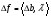 для точки для точки 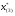 , , 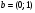 . .Возьмем вектор 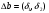 , ему соответствуют множители Лагранжа , ему соответствуют множители Лагранжа 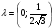 . .Следовательно, 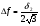 . .Перепишем условие задачи, введя приращение 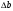 : :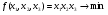 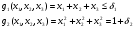 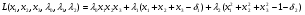 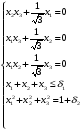  Из первых трех уравнений получаем Из первых трех уравнений получаем 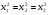 . .Подставим в последнее уравнение: 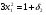 , , 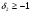 . .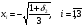 . .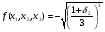 . .Возьмем, например, 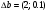 . .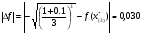 . .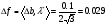 Проверим для 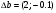 : :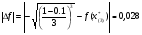 С другой стороны, 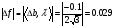 . .
Решение. Перепишем условие следующим образом: 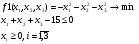 Функция Лагранжа имеет вид: 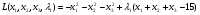 Необходимые и достаточные условия минимума: 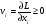 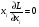 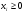 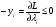 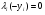 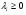 Получаем систему уравнений и неравенств: 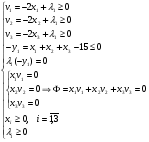 Для решения промежуточной задачи ЛП воспользуемся средствами MS Excel. Введем формулы, соответствующие системе: Зададим начальное приближение: Заполним поля диалога «Поиск решения»: В окне «Параметры» установим флажок «Неотрицательные значения». Результат поиска решения: Найдена седловая точка функции Лагранжа: (х* ,λ*) = (15;0;0;30). Оптимальное решение задачи: х* (15;0;0), f(x*) = 152 = 225. |

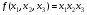 при условиях
при условиях 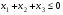 и
и 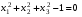 , применяя метод функции Лагранжа. Проверить справедливость оценки изменения целевой функции (14).
, применяя метод функции Лагранжа. Проверить справедливость оценки изменения целевой функции (14).
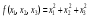 при условиях
при условиях 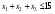 и
и 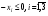 .
.