Теория двойственности в анализе оптимальных решений экономических задач линейного программирования. Теория двойственности в анализе оптимальных решений экономически. Различают три основные формы лп. Стандартная форма
 Скачать 258.54 Kb. Скачать 258.54 Kb.
|
|
Различают три основные формы ЛП. Стандартная форма – все ограничения являются ограничениями-неравенствами, а все переменные неотрицательны (удобна при решении задач ЛП графическим методом). Каноническая форма – все ограничения являются ограничениями-равенствами с неотрицательными правыми частями, а все переменные неотрицательны. Основные вычислительные методы (симплекс-метод и его варианты) разработаны именно для этой формы. Общая форма – часть ограничений являются равенствами, часть – неравенствами. Кроме того, не на все переменные наложены условия не отрицательности. Эти три формы задачи ЛП эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных. Поэтому, если имеется способ решения одной из этих задач, тем самым мы умеем решать любую из трёх задач ЛП. Приведём следующую задачу ЛП, представленную в общей форме, к канонической форме: z=3х1+4х2max, 2х1+3х2=12, 5х1-6х2≤7, -3х1+2х2≤-4, x1 не ограничена в знаке,x20. Проведём следующие преобразования: Т.к. правые части ограничений должны быть неотрицательны, то умножим 3-е ограничение на -1, в результате получим 3х1-2х2≥4. Во 2-м ограничении левая часть не больше правой, поэтому, чтобы их уравнять (сбалансировать), необходимо в левую часть добавить балансовую переменную x30. Если данное ограничение определяет расход некоторого ресурса, переменную x3 следует интерпретировать как остаток, или неиспользованную часть, данного ресурса. В 3-м ограничении левая часть не меньше правой, поэтому, чтобы их сбалансировать, необходимо от левой части отнять балансовую переменную x40. Переменную x4 следует интерпретировать как избыток, или перерасход, данного ресурса. Любую переменную xi, не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных: xi=xi-xi, где xi, xi0. Поэтому в целевой функции и во всех ограничениях необходимо подставить x1=x1-x1, где x1,x10. Указанные операции позволяют привести исходную задачу к канонической форме: z=3x1-3x1+4х2max, 2x1-2x1+3х2=12, 5x1-5x1-6х2+х3=7, 3x1-3x1-2х2+х4=4, x1,x1,x2,x3,x40. Кроме того, необходимо отметить, что максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот. Например, максимизация функции z=3x1-2x2+4х3 эквивалентна минимизации функции (-z)=-3x1+2x2-4х3. Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных x1,x2,x3 в обоих случаях будут одинаковы. Отличие заключается в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны. Теория двойственности в анализе оптимальных решений экономических задач линейного программирования Не менее важным этапом, чем получение оптимального решения по модели задачи, является анализ модели и полученных результатов. В некоторых случаях анализ дает больше информации для принятия решения, чем само решение. Анализ позволяет ответить на вопросы, связанные с повышением рентабельности предприятия, с распределением ограниченных (дефицитных) ресурсов между звеньями производства, с увеличением выпуска продукции путем рациональной расшивки узких мест производства, определения цен на взаимозаменяемую новую технику и др. Анализ на чувствительность дает возможность определить поведение модели в окрестности экстремума, а также пределы изменения исходных параметров, не изменяющих положение экстремума. Это позволяет сформулировать требования к точности исходных данных, а также упростить и уточнить модель, отрубив параметры, незначительно влияющие на конечный результат и уточнив параметры, находящиеся в области высокой чувствительности. И в этом нам поможет понятие двойственности. Рассмотрим основные понятия и выводы специального раздела линейного программирования ─ теорию двойственности на примере задачи планирования производством. С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Пример. Предприятие выпускает четыре вида продукции П1, П2, П3 и П4. Для производства продукции оно располагает тремя ресурсами, запасы которых ограничены величинами 35, 30 и 40 единиц. Удельные затраты на единицу продукции и цена единицы готовой продукции заданы в виде таблицы:
Требуется определить производственную программу предприятия, обеспечивающую максимальный доход. Модель задачи: f = 14х1+ 10х2+ 14х3+ 11х4 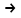 max. (5.1) max. (5.1)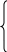 4х1+ 2х2+ 2х3+ 3х4 4х1+ 2х2+ 2х3+ 3х4  35, 35,х1+ х2 + 2х3+ 3х4  30, (5.2) 30, (5.2)3х1+ х2+ 2х3+ х4  40. 40.хj  0, (j= 0, (j=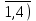 . (5.3) . (5.3)Предположим, что некоторая организация может закупить все ресурсы, которыми располагает предприятие. Необходимо определить оптимальные оценки на эти ресурсы, исходя из естественного условия, что покупающая организация стремится минимизировать общую оценку ресурсов. Нужно, однако, учитывать и тот факт, что за ресурсы покупающая организация должна уплатить сумму, не меньшую той, которую может, выручить предприятие при организации собственного производства продукции. Итак, предположим, что оставаясь в рамках производства в задаче необходимо установить оценки используемых в производстве ресурсов с учетом их влияния на конечный результат производства. Обозначим эти оценки за единицу каждого вида ресурса соответственно через y1; y 2 и y 3 (Р1, Р2, Р3). Эти оценки для упрощения иногда называют внутренними ценами на ресурсы в условиях данного производства (теневыми ценами). Т.е. они представляют объективно необходимые затраты на производство продукции в данных условиях. Понятно, что при их определении следует руководствоваться следующими соображениями: 1. Оценка ресурсов, затрачиваемых на выпуск единицы готовой продукции должна быть не меньше оценки единицы готовой продукции, т.е.  П1: 4у1 + у2 + 3у3  14 14П2: 2у1 + у2 + у3  10 (5.4) 10 (5.4)П3: 2у1 + 2у2 + 2у3  14 14П1: 3у1 + 3у2 + у3  11 112. Оценки по их смыслу должны выражаться не отрицательными числами, т.е. уi  0, i = 0, i = 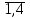 (5.5) (5.5)3. Для объективной оценки ресурсов необходимо требовать, чтобы общая стоимость всех ресурсов, находящихся в распоряжении предприятия, была возможно меньше, т.е. φ = 35 у1 + 30 у2 + 40 у3 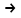 min (5.6.) min (5.6.)Итак, получили модель задачи: φ = 35 у1 + 30 у2 + 40 у3  min min 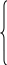 4у1 + у2 + 3у3  14 142у1 + у2 + у3  10 (5.7.) 10 (5.7.)2у1 + 2у2 + 2у3  14 143у1 + 3у2 + у3  11 11уi  0, i = 0, i = 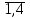 Таким образом, проблема правильной оценки ресурсов находится в распоряжении предприятия и сводится к решению стандартной ЗЛП. Задача (5.7.) называется двойственной к задаче (5.1.) — (5.3). Эти две задачи представляют собой числовой пример пары симметричных двойственных задач. С экономической точки зрения в прямой задаче шла речь о нахождении оптимального плана выпуска продукции при ограничениях ресурсов из условия максимизации выручки. В двойственной задаче речь идет о нахождении системы внутренних цен на используемые в производстве ресурсы, из условия минимизации стоимости всех запасов имеющихся на предприятии. Система двойственных оценок (уi) тесно связана с конкретными условиями данного производства. С изменением этих условий меняется и система этих оценок. В общем виде модели симметричных двойственных задач имеют следующий вид:
Пусть нам дана задача линейной оптимизации в общем виде, тогда двойственная к ней примет вид:
Свойство двойственности является взаимным, т.е. если к задачам (I`) и (II`) записать двойственные, то они совпадут с задачами (I) и (II) соответственно. Любую задачу внутри двойственной пары можно назвать прямой или исходной, тогда другая будет двойственной к ней. Анализируя модели задач двойственной пары, можно сделать следующие выводы о связях, существующих между элементами модели задач двойственной пары: 1. Коэффициентами целевой функции двойственной задачи, являются свободные члены ограничений прямой задачи, а свободными членами ограничений двойственной задачи - коэффициенты целевой функции прямой задачи. В двойственной задаче будет столько переменных, сколько ограничений в прямой и столько ограничений, сколько переменных в прямой задаче. Таким образом, каждому ограничению задачи отвечает соответствующая переменная двойственной задачи и наоборот. 2. Матрицы коэффициентов при переменных в двойственных задачах взаимно транспортированы. 3. Каждому ограничению ─ неравенству в двойственной задаче отвечает неотрицательная переменная, а каждому ограничению равенству ─ переменная произвольного знака и наоборот: каждой неотрицательной переменной ─ ограничение неравенство, а каждой переменной произвольного знака ─ ограничение равенство. При этом в задаче максимизации ограничения-неравенства имеют смысл «  », а в задаче минимизации ─ « », а в задаче минимизации ─ « ». ».4. Если в прямой задаче функция целевая максимизируется, то в двойственной минимизируется и наоборот. Итак, согласно теории линейного программирования каждой оптимизационной задаче линейного программирования соответствует двойственная ей задача. Основные утверждения о взаимодвойственных задачах содержатся в следующих теоремах, называемых теоремами двойственности. | |||||||||||||||||||||||||||

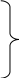 f =
f = 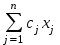
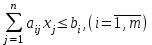 (I)
(I) 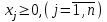
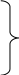 φ =
φ = 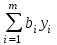
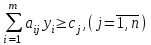 (II)
(II) 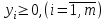
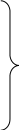 f =
f = 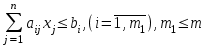
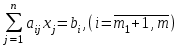 (II)
(II) 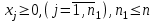
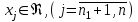
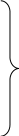 φ =
φ = 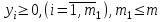
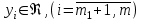 (II`)
(II`)