Теория двойственности в анализе оптимальных решений экономических задач линейного программирования. Теория двойственности в анализе оптимальных решений экономически. Различают три основные формы лп. Стандартная форма
 Скачать 258.54 Kb. Скачать 258.54 Kb.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
| Если одна из двойственных задач имеет оптимальный план, то и другая разрешима, т.е. имеет оптимальный план. При этом экстремальные значения целевых функций совпадают, т.е. fmax=φmin. Если же в одной из задач целевая функция не ограничена на множестве планов, то в другой задаче система ограничений противоречива, т.е. задача не разрешима. |
Рассмотрим экономическое приложение этой теоремы.
В действительности связь между двойственными задачами гораздо глубже, нежели об этом говорится в теореме.
Оказывается, подвергая симплексному преобразованию модель одной из задач, мы тем самым преобразуем и модель двойственной задачи, а поэтому решая одну из задач двойственной пары симплексным методом, мы одновременно решаем и двойственную задачу, так что получив оптимальный план решаемой задачи, мы вместе с этим находим и компоненты оптимального плана двойственной задачи.
Компоненты оптимального плана двойственной задачи находятся в строке целевой функции последней симплексной таблицы решенной задачи. Чтобы правильно выписать компоненты оптимального плана двойственной задачи необходимо учесть соответствие между переменными двойственных задач, устанавливаемое для канонических форм, в котором базисным переменным одной задачи отвечают свободные переменные другой и наоборот.
Рассмотрим наш пример.
| f = 14х1+ 10х2+ 14х3+ 11х4 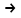 max max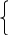 4х1+ 2х2+ 2х3+ 3х4 + х5 = 35, 4х1+ 2х2+ 2х3+ 3х4 + х5 = 35,х1+ х2 + 2х3+ 3х4 + х6 =30, 3х1+ х2+ 2х3+ х4 + х7 = 40. хj  0, (j= 0, (j=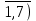 | φ = 35 у1 + 30 у2 + 40 у3 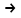 min min 4у1 + у2 + 3у3 – у4 = 14 4у1 + у2 + 3у3 – у4 = 142у1 + у2 + у3 -у5 = 10 2у1 + 2у2 + 2у3 -у6 = 14 3у1 + 3у2 + у3 -у7 = 11 уi  0, i = 0, i = 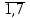 |
Так как исходная задача разрешима, то и двойственная будет иметь оптимальный план, который находится в последней симплексной таблице решенной задачи. Запишем соответствие между переменными задач:
| СП | БП |
    х1 х2 х3 х4 х1 х2 х3 х4 у4 у5 у6 у7 |    х5 х6 х7 х5 х6 х7у1 у2 у3 |
| БП | СП |
Используя данное соответствие из таблицы 6 находим значения двойственных переменных, которые находятся в строке целевой функции под свободными переменными (это у1 х5, у4 х1, у7 х4, у2 х6), а все остальные переменные двойственной задачи будут равны нулю:
у1 х5
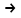 у
у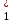 = 3; у2 х6
= 3; у2 х6 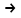 у
у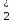 = 4; у3 х7
= 4; у3 х7 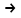 у
у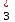 = 0;
= 0;у4 х1
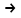 у
у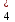 = 2; у5 х2
= 2; у5 х2 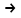 у
у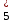 = 0; у6 х3
= 0; у6 х3 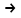 у
у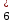 = 0;
= 0;у7 х4
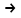 у
у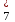 = 10.
= 10.Таким образом можно записать оптимальный план двойственной задачи:
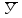 = (3; 4; 0; 2; 0; 0; 10), φmin = 225.
= (3; 4; 0; 2; 0; 0; 10), φmin = 225.С экономической точки зрения теорема 1 означает, что по оптимальному плану выпуска продукции все затраты внутри производства совпадают с оценкой готовой продукции, произведенной по этому плану, т.е. при оптимальном плане вся стоимость затрат внутри производства поглощается в стоимости готовой продукции. Т.е. затраты равны 35*3+30*4+40*0=225. Стоимость готовой продукции 14*0+10*5+14*12,5+11*0=225.
Отсюда вытекает первое свойство двойственных оценок: двойственные оценки уi (i =
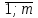 ), — являются инструментом балансирования затрат и результатов.
), — являются инструментом балансирования затрат и результатов.Рассмотрим следствие, вытекающее из первой теоремы, которое представлено в виде второй теоремы двойственности.
Теорема 2 (о дополняющей нежесткости).
| Для того, чтобы планы 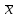 * и * и 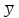 * пары двойственных задач были оптимальными, необходимо и достаточно выполнение условия: * пары двойственных задач были оптимальными, необходимо и достаточно выполнение условия:х 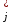 ( (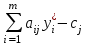 ) = 0, (j = ) = 0, (j = 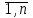 ) (5.8) ) (5.8)у 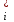 ( (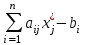 ) = 0, (i = ) = 0, (i = 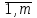 ) (5.9) ) (5.9) |
Условия (5.8) и (5.9) называются условиями дополняющей нежесткости. Из них следует, что если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
В условиях нашего экономического примера это означает, что если ресурс получил положительную оценку (у1 = 3; у2 = 4), то этот ресурс считается дефицитным и весь будет израсходован при реализации оптимального плана. Если же ресурс израсходован не полностью, то его называют избыточным и он получит нулевую оценку (у3 = 0). Отсюда следует вывод или второе свойство двойственных оценок: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку. Причем, чем больше положительное значение двойственной переменной, тем дефицитнее ресурс. В нашем примере наиболее дефицитным ресурсом является ресурс Р2.
Еще можно рассмотреть и другой случай:
х
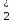 = 5 > 0
= 5 > 0 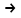 2у
2у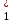 +у
+у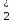 +у
+у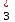 = 2*3+4+1*0=10 = 10
= 2*3+4+1*0=10 = 10т.е. выпуск по этому виду продукции оправдан.
х
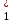 = 0
= 0 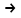 4у
4у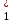 +у
+у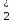 +3у
+3у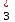 = 4*3+4+3*0 =16 > 14
= 4*3+4+3*0 =16 > 14следовательно, затраты выше, чем стоимость готовой продукции и данный вид продукции не выгодно производить.
В условиях нашего экономического примера данные рассуждения интерпретируется так: в оптимальный план войдут только те виды продукции, затраты на которые внутри производства совпадут со стоимостью готовой продукции, и не войдут те виды, затраты на которые превышают стоимость готовой продукции. Таким образом, оценки позволяют оценить целесообразность выпуска тех или иных видов продукции, т.е. являются мерой убыточности при производстве не выгодных видов продукции (это третье свойство двойственных оценок).
Пример 5. Проверить целесообразность выпуска продукции П5, если удельные затраты ресурсов составляют соответственно 5; 4; 6 условных единиц. Стоимость единицы продукции составляет 25 ден.ед.
Решение. Найдем затраты на производство единицы продукции П5 5у
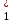 +4у
+4у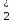 +6у
+6у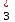 = 5*3+4*4+6*0 = 31 ден.ед. Сравним со стоимостью готовой продукции: 31 > 25. Следовательно производство продукта П5 по такой цене не целесообразно. ■
= 5*3+4*4+6*0 = 31 ден.ед. Сравним со стоимостью готовой продукции: 31 > 25. Следовательно производство продукта П5 по такой цене не целесообразно. ■Теорема 3 (об оценках).
| Компоненты оптимального плана двойственной задачи численно равны частным производным от экстремального значения целевой функции по свободным членам ограничении задачи: у 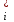 = =  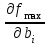 (i= (i=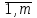 ) (5.10) ) (5.10) |
Оценки показывают как изменяется экстремальное значение функции в зависимости от изменения правых частей ограничений задачи.
На практике теорема чаще всего используется на языке конечных приращений: у
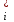
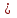
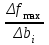 (i=
(i=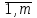 ) (5.11)
) (5.11)В такой записи применительно к нашей экономической задаче оценки показывают, на сколько изменится максимальная выручка предприятия, если запас дефицитного ресурса изменится на единицу. Таким образом, оценки являются мерой влияния ограничений задачи на экстремальное значение целевой функции (четвертое свойство двойственных оценок).
Однако, как это свойство, так и все предыдущие остаются справедливыми до тех пор, пока, правые части ограничений задачи меняются в определенных пределах (пределах чувствительности).
В нашем примере видно, что перспективными ресурсами являются ресурсы Р1 и Р2, т.к. вводя единицу ресурса Р1 в производство дополнительно, мы увеличиваем выручку на 4 денежные единицы.
Пример 6. Предположим, что из производства исключается 2 единицы дефицитного ресурса Р2. Понятно, что выручка снизится. Какое количество взаимозаменяемого ресурса Р1 следует ввести в производство с тем, чтобы возместить уменьшение выручки.
Решение: Выручка (по третьей теореме двойственности) уменьшится на 2*у
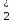 =2*4=8 ден.ед. Эту же величину необходимо возместить за счет введения первого ресурса, т.е. 8=Δb1*у
=2*4=8 ден.ед. Эту же величину необходимо возместить за счет введения первого ресурса, т.е. 8=Δb1*у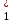 . Отсюда легко находим значение Δb1. Получаем Δb1=8/3. 8/3 единиц первого ресурса заменят недостаток второго. ■
. Отсюда легко находим значение Δb1. Получаем Δb1=8/3. 8/3 единиц первого ресурса заменят недостаток второго. ■Пример 7. Кирпичный завод выпускает кирпичи двух марок (I и II). Для производства кирпича применяется глина трех видов (A, В, С). По месячному плану завод должен выпустить 10 у.е. кирпича марки I и 15 у.е. кирпича марки II. В таблице указаны расход различных видов глины для производства кирпича каждой марки и месячный запас глины:
| Марка | Количество глины, необходимой для производства 1 у.е. кирпича вида | ||
| А | В | С | |
| I | 1 | 0 | 1 |
| II | 0 | 2 | 2 |
| Запас глины | 15 | 36 | 47 |
Сколько у.е. кирпича различных марок должен выпустить завод сверх плана, чтобы обеспечить наибольшую прибыль, если известно, что от реализации 1 у.е. кирпича марки I завод получит прибыль, равную 4 у.е., а от реализации кирпича марки II – 7 у.е.?
Путем графического анализа данной задачи найти решение двойственной к ней и оценить дефицитность исходных ресурсов.
Решение. Составим математическую модель задачи. Обозначим через х1 – количество единиц кирпича марки I, выпущенных сверх плана, а х2 – марки II. Тогда выпуск кирпича марки I составляет (10+х1) единиц, марки II – (15+х2) единиц, а прибыль, получаемая от реализации продукции, составит
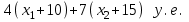
Цель – максимизировать прибыль, следовательно,
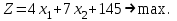
На выпуск продукции будет израсходовано соответственно:
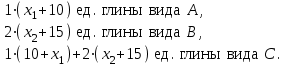
Учитывая запасы глины различных видов на заводе, получаем ограничения:
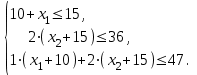
Из условия задачи следует, что
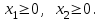
Итак, математическая модель исходной (прямой) задачи имеет вид:
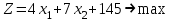
при ограничениях:
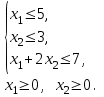
Очевидно, что данная задача может быть решена геометрически (две переменные х1 и х2). Решая задачу графически, нетрудно убедиться, что оптимальным планом этой задачи является:
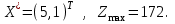
Итак, чтобы получить максимальную прибыль, завод должен выпустить сверх плана 5 у.е. кирпича марки I и 1 у.е. кирпича марки II.
Составим математическую модель двойственной задачи. Поставим в соответствие трем ограничениям-неравенствам прямой задачи переменные:
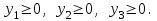
Тогда математическая модель двойственной задачи примет вид:
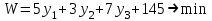
при ограничениях:
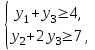
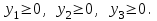
Согласно первой теореме двойственности
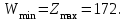
Далее, используя вторую теорему двойственности, найдем оптимальный план Y*=(у1*, у2*, у3*) двойственной задачи, в котором у1*, у2*, у3*являются оптимальными оценками ресурсов (глина видов А, В и С). Так как х1*=5>0, то согласно второй теореме, ограничение
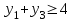 в двойственной задаче ее оптимальным планом должно обратиться в равенство, т.е.
в двойственной задаче ее оптимальным планом должно обратиться в равенство, т.е. 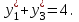 Аналогично из того, что
Аналогично из того, что 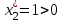 , следует у2*+2у3*=7. Итак, имеем систему уравнений:
, следует у2*+2у3*=7. Итак, имеем систему уравнений: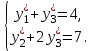
Кроме того, в оптимальном плане
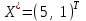 первое и третье ограничения прямой задачи выполняются как равенства (5=5; 5+2·1=7). Это означает, что глина видов А и С используется полностью, являясь дефицитной. Дальнейшее увеличение запасов глины видов А и С целесообразно. Если же ресурс расходуется не полностью, то он избыточен, его дальнейший рост не повлияет на эффективность работы завода. Таким ресурсом является глина вида В. Действительно, так как второе ограничение
первое и третье ограничения прямой задачи выполняются как равенства (5=5; 5+2·1=7). Это означает, что глина видов А и С используется полностью, являясь дефицитной. Дальнейшее увеличение запасов глины видов А и С целесообразно. Если же ресурс расходуется не полностью, то он избыточен, его дальнейший рост не повлияет на эффективность работы завода. Таким ресурсом является глина вида В. Действительно, так как второе ограничение 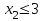 в оптимальном плане
в оптимальном плане 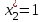 выполняется как строгое неравенство 1 < 3, то глина вида В избыточна, и согласно второй теореме двойственности ее оценка равна нулю (у2*=0).
выполняется как строгое неравенство 1 < 3, то глина вида В избыточна, и согласно второй теореме двойственности ее оценка равна нулю (у2*=0).Из системы находим
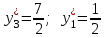 .
.Получим
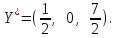
Тогда
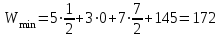 ,
,что совпадает с экстремальным значением функции W, уже найденным с помощью первой теоремы двойственности.
Кроме того, замечаем, что глина вида С является более дефицитной, чем глина вида А, так как
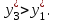
Задания общие для всех:
Модель двойственной задачи построенной к данной
f = 8х1 - 4х2+ 7х3
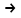 max.
max.  2х1+ 3х2 - 4х3
2х1+ 3х2 - 4х3  106,
106,5х1+ 4 х2 + х3
 205,
205, 4х1+ 2х2+ 8х3
 340.
340.хj
 0, (j=
0, (j=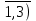 .
. принимает следующий вид:
| 1) φ = 8 у1 – 4 у2 + 7 у3  min min  2у1 + 3 у2 – 4у3  106 1065у1 +4 у2 + у3  205 205 4у1 + 2у2 + 8у3  340 340уi  0, I = 0, I = 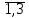 | 2) φ = 106 у1 + 205 у2 +340 у3 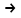 min min  2у1 + 5 у2 + 4у3  8 83у1 +4 у2 + 2 у3  -4 -4 -4у1 + у2 + 8у3  7 7уi  0, i = 0, i = 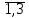 |
| 3) φ = 106 у1 + 205 у2 +340 у3  max max  2у1 + 5 у2 + 4у3  8 83у1 +4 у2 + 2 у3  -4 -4 -4у1 + у2 + 8у3  7 7уi  0, I = 0, I =  | 4) φ = 8 у1 - 4 у2 + 7 у3  max max  2у1 + 3 у2 - 4у3  106 1065у1 +4 у2 + у3  205 205 4у1 + 2у2 + 8у3  340 340уi  0, i = 0, i =  |
При решении пары двойственных задач (одна из которых задача об оптимальном использовании ресурсов) получен следующий результат:
f(
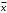 ) = 20x1+10x2+9x3 (max);
) = 20x1+10x2+9x3 (max); 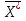 =(10; 0; 3; 0; 8; 0);
=(10; 0; 3; 0; 8; 0); 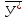 =(2; 0; 4; 0; 5; 0). Значение прибыли, если в производство ввести 3 единицы наиболее дефицитного ресурса, будет равно
=(2; 0; 4; 0; 5; 0). Значение прибыли, если в производство ввести 3 единицы наиболее дефицитного ресурса, будет равно| 1) | 2) | 3) | 4) | 5) |
| 251 | 233 | 242 | 239 | другой ответ |
3) Оцените целесообразность включения в план нового вида продукции, нормы затрат ресурсов на единицу которого равны соответственно 3, 4, 2, а прибыль от реализации равна 40 ден.ед., если при решении задачи о производстве продукции при оптимальном использовании ресурсов было получено следующее решение
| f( 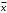 ) = 5x1+3x2+x3 (max) ) = 5x1+3x2+x3 (max)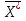 (5; 0; 24; 4; 0; 0) (5; 0; 24; 4; 0; 0)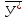 (0; 9; 3; 0; 2; 0). (0; 9; 3; 0; 2; 0). | нецелесообразно; данное задача не разрешима; целесообразно. |
Оцените целесообразность закупки 10 единиц второго вида ресурса по цене 2,5 ден.ед., если при решении задачи о производстве продукции при оптимальном использовании ресурсов было получено следующее решение
| f( 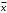 ) = 46x1+25x2+30x3 (max) ) = 46x1+25x2+30x3 (max)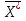 (500;405; 0; 0; 0; 20) (500;405; 0; 0; 0; 20)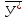 (4; 3; 0; 0; 0; 8). (4; 3; 0; 0; 0; 8). | нецелесообразно; данное задача не разрешима; целесообразно. |
5) Сформулируйте двойственные задачи для:
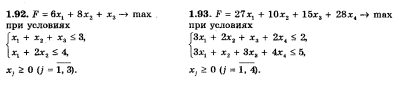
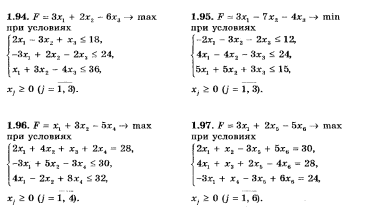
И представьте их в виде тестов с 3-мя неправильными и 1 правильным ответом.
