1. Исследование функции на безусловный экстремум 3
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
      ОглавлениеТеоретическая часть 3 1.Исследование функции на безусловный экстремум 3 2. Численные методы безусловной минимизации 5 Метод конфигураций (Хука-Дживса) 7 Метод деформируемого многогранника (Нелдера-Мида) 7 Метод дробления шага 8 Метод наискорейшего градиентного спуска 8 Метод сопряженных направлений (Флетчера – Ривса) 9 Метод Ньютона 9 Порядок выполнения лабораторной работы 10 Пример выполнения лабораторной работы 10 3. Решение задачи минимизации со смешанными ограничениями 17 Седловые точки функции Лагранжа 19 Метод седловой точки в задачах квадратичного программирования 21 Метод проекции градиента для задачи условной оптимизации 22 Метод условного градиента для задачи условной оптимизации 22 Метод возможных направлений для задачи условной оптимизации 23 Порядок выполнения лабораторной работы 23 Пример выполнения лабораторной работы 24 4. Основные понятия линейного программирования 34 Модель задачи линейного программирования 34 Свойства задачи линейного программирования 36 Двойственность в линейном программировании 37 5. Задача транспортного типа 39 Построение модели транспортной задачи 39 Методы нахождения начального плана перевозок. 42 Метод потенциалов 43 Контрольные задания 45 Задание 1. Линии уровня 46 Задание 2. Числовые характеристики симметричной квадратной матрицы. 46 Задание 3. Формула Тейлора для функции нескольких переменных 47 Задание 4. Нахождение локальных экстремумов 47 Задание 5. Одномерная оптимизация 47 Задание 6. Многомерная оптимизация по направлению 47 Задание 7. Методы безусловной оптимизации 48 Контрольные вопросы 48 Задание 8. Методы условной оптимизации 48 Контрольные вопросы 49 Задание 9. Задача линейного программирования и симплекс-метод 49 Задание 10. Транспортная задача 49 Литература 50 Приложение. Рекомендации по использованию EXCEL и MATLAB 51 П1. Построение графиков 51 П2. Действия с матрицами 52 Теоретическая часть1.Исследование функции на безусловный экстремумРассматривается задача  f(x)→ extr, x f(x)→ extr, x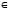 En. (1) En. (1)Метод поиска безусловного экстремума основывается на следующих условиях оптимальности:
Пусть функция f(x) дифференцируема в точке х* 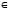 Еn. Тогда если х* локальное решение задачи (1), то Еn. Тогда если х* локальное решение задачи (1), то gradf(x*)=0 (2)
Пусть функция f(x) дважды дифференцируема в точке х* 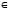 Еn. Тогда Еn. Тогда
Пусть функция f(x) дважды дифференцируема в точке х* 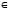 Еn и gradf(x*)=0. Еn и gradf(x*)=0.
Если gradf(x*)=0, то х* называется стационарной точкой.Для выпуклой (вогнутой) на Еn функции стационарные точки являются точками ее глобального минимума (максимума). Строго выпуклые (вогнутые) функции имеют единственный глобальный минимум (максимум). Критерий выпуклости функции. Дважды непрерывно дифференцируемая на выпуклом множестве Х с непустой внутренностью функция является выпуклой (вогнутой) на этом множестве в том и только том случае, когда матрица Гессе Н(х*) неотрицательно (неположительно) определена для всех х 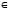 Х. Х.При исследовании на знакоопределенность матрицы вторых производных функции рекомендуется применять критерий Сильвестра или анализ собственных значений матрицы. Схема поиска безусловных экстремумов функции:
|

 р
р р
р