1. Исторические начала квантовой механики
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
1. Исторические начала квантовой механики квантовый механика микрочастица волновой Считается, что квантовая физика, сыгравшая принципиально важную роль в развитии науки и техники, появилась в ХХ столетии. К этому времени классическая физика столкнулась с непреодолимыми трудностями при рассмотрении электромагнитного излучения нагретых тел. Предположение о том, что изменение энергии излучения происходит непрерывно, привело к теоретическим результатам, противоречащим данным экспериментов в области коротковолнового диапазона излучения. В 1900 году решение этой проблемы предложил Макс Планк, выдвинув принципиально новую гипотезу о том, что энергия излучения осуществляется дискретными порциями - квантами. Основанная на этой гипотезе квантовая теория излучения позволила Планку непротиворечивым образом описать равновесное тепловое излучении во всем диапазоне длин волн. Вместе с тем, сам Планк рассматривал квантование не иначе, как математический прием решения задачи об испускании и поглощении. Альберт Эйнштейн, развивая гипотезу о квантах, выдвинул корпускулярную теорию, в которой электромагнитное излучение не только порождается, но и существует с промежутках между поглощением и испусканием в виде потока квантов, названных фотонами (1905). Фотонная теория позволила объяснить явления квантовой оптики. В 1924 году Луи де Бройль выдвинул радикальную гипотезу о волновом характере материи. Он предположил, что электромагнитные волны (фотоны) могут вести себя как частицы, а частицы - как волны. Такая двойственность, получившая название корпускулярно-волнового дуализма, приводит к существенным отличиям в описании движения микрочастиц в квантовой механике по сравнению с классической механикой. В частности, Дж. фон Нейман попытался сблизить квантовую теорию с классической механикой, и составил уравнение, дающее математическое описание материи с помощью терминов волновой функции. Так возникла волновая механика. Незадолго до этого Вернер Гейзенберг, Макс Борн и Паскуаль Иордан опубликовали вариант квантовой теории, получивший название матричной механики, которая описывала квантовые явления с помощью таблиц наблюдаемых величин. Эти таблицы представляют собой определенным образом упорядоченные математические множества, называемые матрицами, над которыми по известным правилам можно производить различные математические операции. Матричная механика позволяла достичь согласия с наблюдаемыми экспериментальными данными, но в отличие от волновой механики не содержала никаких конкретных ссылок на пространственные координаты или время. Согласно доказательству Шрёдингера, волновая механика и матричная механика математически эквивалентны. Окончательное формирование квантовой механики как последовательной теории связано с работой Вернера Гейзенберга 1927 года, в которой был сформулирован принцип, утверждающий, что любая физическая система не может находиться в состояниях, в которых координаты ее центра инерции и импульс одновременно принимают вполне определенные, точные значения. Этот принцип получил название "соотношение неопределённостей". Известные ныне под общим названием квантовой механики, вышеперечисленные достижения дали долгожданную общую основу описания квантовых явлений. 2. Фундаментальные понятия квантовой механики .1 Гипотеза де Бройля И волновые, и корпускулярные свойства частиц нашли очень широкое применение при изучении различных физических явлений. В 1924 г. Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. По гипотезе де Бройля каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы, остаются такими же, как и в случае электромагнитного излучения. Таким образом, если частица имеет энергию E и импульс, абсолютное значение которого равно p, то с ней связана волна, распространяющаяся в том же направлении, что и частица, и описывающая ее волновые свойства. Частота этой волны описывается формулой: 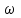 = E / = E / 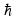 , ,а её длина: λ = 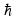 / / 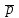 , ,где 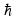 - постоянная Планка. Эта волна и получила название волны де Бройля. - постоянная Планка. Эта волна и получила название волны де Бройля.Соотношения, связывающие корпускулярные и волновые свойства частицы, = 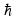 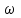 , , 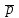 = = 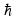 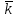 где 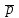 - это импульс частица, а - это импульс частица, а 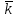 - волновое число, получили название уравнений де Бройля. - волновое число, получили название уравнений де Бройля.Экспериментальным подтверждением гипотезы де Бройля послужили экспериментальные исследования дифракции электронов на кристаллической решетке. Следует отметить, что т.к. длина волны де Бройля электрона имеет порядок, совпадающий с порядком расстояния между атомными плоскостями в кристалле (около 10-10 м), кристалл может играть роль дифракционной решетки для электронных волн. Наиболее значительными оказались экспериментальные результаты, полученные в ходе исследования дифракции электронов на совершенном кристалле (кристалле, обладающем идеальной кристаллической решеткой). Они показали состоятельность условия Вульфа-Брэгга, а именно появление дифракционного максимума тогда, когда разность хода волн, отраженных от соседних атомных плоскостей, равна целому числу длин волн де Бройля. Именно в этом случае волны усиливают друг друга, т.е. имеет место конструктивная интерференция. .2 Принцип неопределённостей Гейзенберга Открытие волновых свойств у микрочастиц показывает, что в физике микромира мы имеем дело с принципиально новым объектом исследований. Отличие микрочастицы от волны состоит в том, что волну, используя, например, зеркало, можно разделить на две части и отдельно исследовать каждую из них. Микрочастица же, например, электрон или нейтрон, во всех опытах проявляется как единое целое. Никому еще не удавалось наблюдать пол-электрона или четверть нейтрона, и т.д. Важное отличие квантовой механики от остальных теорий состоит в том, что в классических теориях описываются свойства объектов вне их отношения к тем приборам, с помощью которых обнаруживаются эти свойства, в то время как в квантовой механике учет условий наблюдения неотъемлем от самой теоретической постановки проблемы (при этом в различных макроскопических ситуациях микроявления обнаруживают различные, порой прямо противоположные свойства, например, частицы или волны). Вследствие этого мы имеем право говорить об изменении понятия наблюдения за микрочастицей. Действительно, наблюдение - это процесс взаимодействия объекта с прибором В 1998 г. такой эксперимент был проведен с пучком атомов, которые последовательно пересекали систему из двух стоячих световых волн. Стоячие волны играли роль интерференционных решеток, после прохождения которых атомный пучок расщеплялся на четыре когерентных пучка. Эти пучки интерферировали между собой. С помощью дополнительных устройств, представляющих собой резонаторы с лазерным излучением, можно было получить информацию о пути атомного пучка до и после прохождения им световой решетки. Опыт показал, что при включении резонаторов интерференционная картина исчезала, а при выключении - вновь появлялась. Частицы будто бы чувствовали, что за ней наблюдают. Явление исчезновения интерференции при включении дополнительных приборов наблюдения получило название декогеренции. Важно, что декогеренция может наблюдаться даже в том случае, когда наблюдение не организуется намеренно, а является результатом взаимодействия частицы с ее окружением. Таким образом, понятие траектории становится неприменимым по отношению к квантовой частице. Рассмотрим в качестве примера дифракцию электронов на щели. Пусть электроны падают нормально на непрозрачный экран, в котором имеется щель (рис. 1) 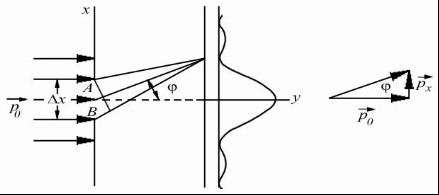 Рис. 1 - Картина дифракции электронов на щели Дифракционная картина фиксируется фотопластинкой, расположенной за экраном. Пусть падающие электроны обладают определенным импульсом p. Тогда, согласно квантово-механическим представлениям, этим электронам соответствует плоская волна с волновым вектором 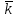 , определяемым из уравнений де Бройля. Поскольку волна распределена по всему пространству, каждый электрон до прохождения через щель имеет точно определенный импульс и неопределенную координату x. При прохождении электрона через щель ситуация меняется. Неопределенность координаты x становится равной ширине щели , определяемым из уравнений де Бройля. Поскольку волна распределена по всему пространству, каждый электрон до прохождения через щель имеет точно определенный импульс и неопределенную координату x. При прохождении электрона через щель ситуация меняется. Неопределенность координаты x становится равной ширине щели 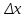 , но при этом появляется неопределенность проекции импульса , но при этом появляется неопределенность проекции импульса 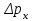 , обусловленная дифракцией электронов на щели. , обусловленная дифракцией электронов на щели. Дело в том, что электроны, прошедшие через щель на экране, описываются уже не плоской, а расходящейся волной, интенсивность которой зависит от угла дифракции. Мы приходим к выводу: если мы пытаемся насильно избавить электрон от неопределённости в координате, то мы неизбежно увеличиваем неопределённость в импульсе Закон имеет вид: 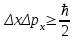 , ,И его словесная формулировка такова: Улучшая наше знание о какой-либо одной характеристике частицы, мы ухудшаем наше знание о дополнительных её характеристиках. Наш эксперимент над электроном продемонстрировал неустранимое «квантовое дрожание» (обычно говорят: нулевые колебания Например, даже при нулевой температуре 2.3 Квантовое состояние, сцепленность Проблемы квантовых измерений влекут за собой ряд феноменов квантовой теории, которые следуют из необычных свойств изучаемых частиц. Квантовой сцепленностью называется квантовомеханическое 3. Эксперимент над квантовомеханической системой .1 Особенности описания движения микрочастиц Хорошо исследованный аппарат классической аналитической механики не подходит для описания движения микрочастиц, поскольку частицы в квантовой механике обладают как корпускулярными, так и волновыми свойствами. Микрочастицами принято считать частицы, длина волны де Бройля, которых сравнима или больше характерного размера области движения, поэтому в квантовой механике речь идет о микрочастицах. В классической механике полный набор обобщенных координат и импульсов характеризует состояние механической системы. Изменение механического состояния во времени приводит нас к понятию траектории. Однако в квантовой механике координата и импульс подчиняются каноническому коммутационному соотношению. Отсутствие возможности задать состояние микрочастицы классическим образом привело исследователей к парадоксальному заключению об отсутствии траектории движения микрочастиц. Волновая формулировка квантовой механики Шредингера позволяет описывать квантово-механическое состояние при помощи комплексной волновой функции. В 1926 году было выведено уравнение, описывающее пространственно-временное изменение состояния, заданного волновой функцией. Такое уравнение можно назвать нерелятивистским уравнением движения для микрочастицы. Уравнение Шредингера играет в квантовой механике Уравнение Шредингера нашло применение для решения широкого круга задач квантовой механики. Например, результаты расчёта Н. Бора для частот и основных значений энергии при исследовании атома водорода были подтверждены в 1925-1926 гг. полным квантово-механическим анализом, с использованием уравнения Шредингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра может быть найдено в аналитической форме. Из него получают уровни энергии Также при помощи уравнения Шредингера решаются задачи о движении частиц в потенциальных ямах, задача о туннелировании. Важно отметить, что из уравнения Шредингера можно предельным переходом получить уравнение Ньютона. В этом смысле квантовая механика при описании движения микрочастиц не требует полного отказа от классической механики, а лишь определяет ее границы. Однако уравнение Шрёдингера предназначено для частиц без спина, движущихся со скоростями много меньшими скорости света Первым из таких обобщений стало уравнение Клейна-Гордона-Фока, которое описывает быстро движущиеся частицы, имеющих массу (массу покоя). Оно строго применимо к описанию скалярных массивных полей. Может быть обобщено для частиц с целым и полуцелым спинами. Кроме прочего, ясно, что уравнение Клейна-Гордона-Фока является обобщением обычного волнового уравнения Однако уравнение Клейна-Гордона-Фока не удовлетворяет в полной мере экспериментально наблюдаемым явлением, поэтому для строгого описания движения релятивистских частиц с полуцелым спином применяется уравнение Дирака. Именно уравнение Дирака помогло объяснить спин, который приписывался электронам. На основе уравнения Дирака были найдены формулы для вероятностей рассеяния фотонов Кроме того, волновая функция может описывать только чистые состояния, поэтому для описания смешанных состояний квантовых систем была введена матрица плотности. Для матрицы плотности введены фундаментальные эволюционные уравнения: Уравнение Гейзенберга Уравнение фон Неймана Уравнение Линдблада 3.2 Основные принципы проведения измерений В квантовой механике измерение - это концепция, которая описывает возможность получения информации Исходя из такой трактовки развивалась матричная формулировка квантовой механики, основанная на введенном Гейзенбергом понятии наблюдаемой физической величины. Поэтому результаты любого измерения в квантово-механических системах должны интерпретироваться как значение некоторой физической величины, которой ставится в соответствие оператор физической величины - наблюдаемой. Результаты измерения - это собственные значения рассматриваемых операторов. Полный набор собственных значений называется спектром оператора. При рассмотрении модели идеализированного «абсолютно точного» измерения могут быть получены только лишь такие значения физической величины, которые принадлежат спектру Характерным примером такой концепции является классический опыт Штерна-Герлаха. Собственными значениями оператора проекции спина Поэтому в эксперименте Штерна-Герлаха Поскольку квантовая механика - статистическая теория, обработка результатов измерений зачастую требует привлечения мощного аппарата теории вероятности. Наиболее важным направлением в экспериментальном исследовании квантовых систем являются ансамблевые измерения. Суть состоит в приготовлении и измерении большого числа частиц, находящихся в схожих квантовых состояний. Поскольку точность измерения напрямую зависит от количества приготовленных частиц, существует возможность проведения сверхточных экспериментов в квантовой механике. 4. Парадоксы квантовой теории .1 Парадокс ЭПР В 1935 г. Эйнштейн, Подольский и Розен предложили мысленный эксперимент, из которого, по их мнению, следовало, что для описания физических объектов волновой функции недостаточно. Тем самым, утверждалось, что квантовая механика неполна. Эйнштейн, Подольский и Розен рассмотрели систему двух коррелированных частиц, т.е. таких частиц, свойства которых связаны, не будучи точно заданными. Например, частицы А и Б рождаются в одной точке, а затем разлетаются в разные стороны. В момент рождения ни у одной из них не заданы координата и импульс, но в силу закона сохранения импульса сумма их импульсов, как и сумма их координат, всегда равна нулю. Теперь, если мы проведем измерение над частицей А, например, измерим ее координату, то ее волновая функция "схлопнется" в соответствующей точке. Но в то же время "схлопнется" и волновая функция частицы Б, поскольку ее координата после такого измерения тоже станет известной точно. Если волновая функция полностью характеризует частицу, то значит, с частицей Б действительно что-то произойдет, а ведь измерение проводилось над частицей А, которая могла быть в этот момент очень далеко от частицы Б. А если изменится только волновая функция частицы Б, а сама частица останется точно такой же, значит, волновая функция - плохая характеристика квантовой частицы. В этом и заключается парадокс Эйнштейна-Подольского-Розена или, сокращенно, парадокс ЭПР. Разрешение парадокса состоит в следующем. В действительности, рассуждение, предложенное Эйнштейном, Подольским и Розеном, нисколько не опровергает квантовую механику и даже концепцию волновой функции. Дело в том, что, как стало ясно уже после выхода статьи ЭПР, коррелированные частицы характеризуются лишь одной общей волновой функцией; каждой же из двух частиц определенную волновую функцию приписать нельзя. Поэтому в момент измерения над одной частицей действительно меняется как общая волновая функция обеих частиц, так и соответствующий квантовый объект - две коррелированные частицы. Парадокс ЭПР имел большое значение для развития квантовой теории. Прежде всего, он стимулировал развитие ряда новых понятий и вызвал интерес к коррелированным состояниям квантовых частиц. Когда такие состояния были обнаружены экспериментально для фотонов, началось бурное развитие новой области в физике - квантовой оптики. Кроме того, эксперименты с коррелированными парами квантовых частиц (их также называют ЭПР-парами) позволили проверить, действительно ли вероятностное поведение характерно для отдельной квантовой частицы или это свойство совокупности частиц. 4.2 Редукция фон Неймана. Кот Шрёдингера Для того, чтобы увидеть, как на самом деле изменяются параметры рассматриваемой квантовомеханической системы (например, электрон - прибор), нам понадобилась характеризующая ее волновая функция, или функция состояния. Когда мы начали измерять характеристику квантовой частицы, функция мгновенно изменилась. Этот эффект носит название редукции фон Неймана. В 1971 году Джон фон Нейман развил свою идею о том, что в каждом квантовомеханическом измерении наличествует неанализируемый элемент. Он постулировал, что волновая функция, помимо непрерывного изменения, при измерении претерпевает мгновенное изменение, обусловленное вмешательством наблюдателя, его воздействием на объект. С коллапсом волновой функции, а также неполнотой квантовой механики при переходе от субатомных систем к макроскопическим, непосредственно связан мысленный эксперимент, предложенный Эрвином Шрёдингером. Суть его такова: В закрытый ящик помещён кот Вопрос стоит так: когда система перестаёт существовать как смешение двух состояний и выбирает одно конкретное? Цель эксперимента - показать, что квантовая механика неполна без некоторых правил, которые указывают, при каких условиях происходит коллапс волновой функции Заключение В классической физике Ньютона, Галилея и даже Эйнштейна было одно общее свойство - все физические величины можно было не только измерить, но и с любой степенью точности вычислить их последующие изменения во времени. Поведение любой, сколь угодно сложной, системы и движение тел любой массы и размера были в принципе предсказуемы. Квантовая механика предложила принципиально иную систему законов, управляющих миром. Первые изученные ею микрообъекты - атомы, электроны и фотоны, категорически не желавшие вести себя как классические, заставили физиков кардинально изменить методы описания природных явлений. В классическом естествознании возникли большие трудности с объяснением целого ряда явлений. Понимание того, что микромир живет по особым законам, формировалось постепенно и происходило с большим трудом, поскольку очень уж необычными были эти законы. Проблемы измерений в квантовой механике перестают быть проблемами тогда, когда мы понимаем, что мир не обязан описываться в рамках единого универсального подхода. А это значит, что, двигаясь по пути, указанному квантовой механикой, можно постичь все удивительное богатство и уникальность устройства окружающего мира. Использованные источники 1. Гейзенберг В., Шредингер Э., Дирак П.А.М., Современная квантовая механика. Три нобелевских доклада, М.: Гостехиздат, 1934. 2. Ландау Л.Д., Лифшиц Е.М. Краткий курс теоретической физики, том 2: Квантовая механика. М.: Наука, 1972. . Смирнов Е.В., Мартинсон Л.К. Квантовая физика, М.: МГТУ им. Н.Э.Баумана, 2009. . Паули В. Труды по квантовой теории. Квантовая теория. Общие принципы волновой механики. Статьи 1920-1928. М.: Наука, 1975. . Фейнман Р., Лейтон Р., Сэндс М., Фейнмановские лекции по физике, том: Квантовая механика часть 1, М.: Мир, 1966. . http://ru.science.wikia.com/wiki/Квантовая_механика . http://nrc.edu.ru/est/r2/1.html |
