физика. Законы Ньютона в классической механике
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
Динамика материальной точки Для составления «механических» уравнений движения в физике разработаны общие и достаточно простые методы, однако опять-таки требуется введение некоторых упрощающих предположений (моделей). Одним из важных является представление об изолированной и замкнутой системах. Система частиц (тел) называется замкнутой или изолированной, если каждая из частиц системы не взаимодействует ни с какими внешними телами. Например, с высокой точностью изолированной можно считать Солнечную систему, с некоторыми допущениями – систему «биллиардный стол +шары» и т.п. Законы Ньютона в классической механике. Роль законов Ньютона в физике необозримо велика. На основе ограниченного числа законов построена целая наука – механика, скоро 300 лет используемая человечеством в своей практической и научной деятельности. Первый закон Ньютона – закон инерции нами уже сформулирован. При рассмотрении второго закона Ньютона нужно учесть, что изолированная система – это всё-таки абстракция. Реальные системы, как правило, неизолированные. Например, пока не существует способов экранирования от сил тяготения, чрезвычайно трудно избавиться от влияния сил трения и т.д. Пусть имеется некая неизолированная система. Тогда её импульс со временем будет обязательно изменяться. Производная импульса частицы по времени называется силой, действующей на частицу со стороны её окружения. Иначе быстрота изменения импульса частицы со временем численно равна внешней силе, действующей на эту частицу. 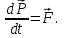 Сила выполняет функцию количественной меры взаимодействия тел друг с другом. Сила будет полностью охарактеризована, если заданы её величина и направление, а также указано, на что и со стороны чего сила действует. Записанное выше соотношение и выражает второй закон Ньютона, один из фундаментальных законов физики. Его легко трансформировать к более широко известному (школьному) виду: 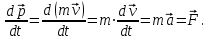 При решении практических задач широкое применение находит «импульсная» формулировка закона: 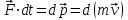 . .Здесь слева – импульс силы, справа – изменение импульса тела. Необходимо заметить, что вынесение массы за знак дифференцирования, как константы, возможно лишь при малых скоростях движения, т.е. когда V< Третий закон Ньютона. Для вывода третьего закона Ньютона рассмотрим изолированную систему, состоящую только из двух взаимодействующих тел. Полный импульс такой системы составляет 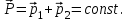 . Продифференцируем это уравнение по времени и учтем закон сохранения импульса . Продифференцируем это уравнение по времени и учтем закон сохранения импульса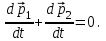 Из II-го закона Ньютона 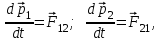 где F12 – сила, действующая со стороны второго тела на первое, а F21 – сила, с которой первое тело действует на второе. Их еще называют силами действия и противодействия. Мы получили III-ий закон Ньютона: 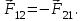 Следует учитывать, что третий закон Ньютона строго выполняется лишь для статических и контактных взаимодействий. Дело в том, что сигнал взаимодействия распространяется с конечной скоростью: в вакууме со скоростью света, в твердом теле – со скоростью продольной волны. Закон сохранения импульса Рассмотрим открытую систему, состоящую из произвольного числа тел.          Продифференцируем последние уравнения по времени: V'x=Vx - V0, где V'x=Vx - V0 – закон сложения скоростей. V'y=Vy (10.2) V'z=Vz t'=t Продифференцировав последние уравнения по времени еще раз, получим: F'x=Fx F'y=Fy F'z=Fz t'=t ɑ'x=αx ɑ'у=αу ɑ'z=αz t'=t или, после умножения на массу m: (10.3) Из уравнений (10.3) следует, что ускорения и силы в инерциальных системах одинаковы.    Механическая работа. Мощность. Механическая энергия. Физическая величина силы тесно связана с другой очень важной величиной – величиной работы. Из курса физики средней школы известно, что, если на частицу, движущуюся по прямой линии, действует сила F, направленная под углом к направлению движения (рис.6.1), то работа силы при перемещении частицы равна A = Frcos, где r – перемещение тела.   F F   r r  r Рис.6.1. К понятию механической работы. В векторных обозначениях это выражение можно записать так: 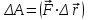 , здесь , здесь 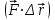 - скалярное произведение векторов - скалярное произведение векторов 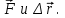 Единицей работы является в Си 1Дж = 1Н1м. Единицей работы является в Си 1Дж = 1Н1м.З  аписанные формулы справедливы только в случае постоянной силы и прямолинейного движения частицы. Рассмотрим более сложный случай движения по бесконечно малому участку траектории произвольного вида, заключенному между бесконечно близкими точками пространства, описываемыми радиус-векторами аписанные формулы справедливы только в случае постоянной силы и прямолинейного движения частицы. Рассмотрим более сложный случай движения по бесконечно малому участку траектории произвольного вида, заключенному между бесконечно близкими точками пространства, описываемыми радиус-векторами 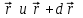 (рис.6.2). (рис.6.2).` ` Рис.6.2. Определение величины работы при дви- жении тела по сложной траектории. Предположим, что в точке 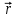 на частицу действует сила на частицу действует сила 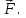 Вследствие малости перемещения мы можем пренебречь изменением силы на нем ( в противном случае ничто нам не помешает сделать более мелкое разбиение!). Кроме того, разбиение нужно продолжать до тех пор, пока сам участок пути не перестанет отличаться от вектора Вследствие малости перемещения мы можем пренебречь изменением силы на нем ( в противном случае ничто нам не помешает сделать более мелкое разбиение!). Кроме того, разбиение нужно продолжать до тех пор, пока сам участок пути не перестанет отличаться от вектора 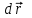 (т.е. пока касательная к траектории не совпадет с хордой дуги). Можно будет считать, что частица движется прямолинейно вдоль (т.е. пока касательная к траектории не совпадет с хордой дуги). Можно будет считать, что частица движется прямолинейно вдоль 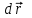 . Тогда к этому бесконечно малому отрезку можно применить формулу, определяющую величину элементарной работы, совершаемой силой F: . Тогда к этому бесконечно малому отрезку можно применить формулу, определяющую величину элементарной работы, совершаемой силой F: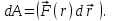 Работа на любом конечном участке траектории, заключенном между точками ro` и r`, определяется суммой всех элементарных работ, производимых при данном перемещении. Эта сумма равна 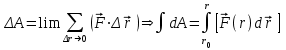 и называется интегралом работы. и называется интегралом работы.Графически работу можно представить площадью под графиком F = F(r) (рис.6.3).   F F(r) F F(r)  A  0 r0` r` r 0 r0` r` rРис. 6.3. К определению интеграла работы. Мощность. Мощностью называется работа, производимая в единицу времени. Если перемещение 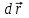 осуществляется за время dt, то мощность равна осуществляется за время dt, то мощность равна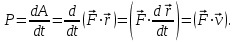 Эта Р – мгновенная мощность. Чаще определяют среднюю мощность 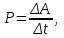 и измеряют её в ваттах, и измеряют её в ваттах,1Вт =1Дж/с. Механическая энергия. Понятно, что получение механической энергии требует затраты некоторых ресурсов. Таким источником работы является запас энергии системы. Энергией системы, в принципе, является запас работы, которую эта система может совершить (а может и не совершить). При этом в механике различают потенциальную и кинетическую энергию. Потенциальная энергия. Ранее мы установили, что работа силы вычисляется суммированием по многим точкам, т.е. по многим состояниям системы. В общем случае работа зависит от того, каким образом меняется состояние (изменение состояниясистемы называется процессом, так что работа является функцией процесса, это особенно ярко проявляется в термодинамике). Если речь ведется о перемещении тела в пространстве, то в общем случае работа зависит от формы и длины траектории. Однако оказывается, что не всегда. Существуют силы, работа которых точно определяется лишь начальным и конечным состояниями частицы, и форма траектории на величину работы не влияет. Такие силы называются потенциальными или консервативными. z  Рис.6.4. К определению понятия потенциаль-   C ного поля сил. C ного поля сил.    A B A Bro D r1   x xy На рис.6.4 изображены участки АСВ и ADB двух траекторий, соединяющих одни и те же точки А и В. Если интеграл силы (работа) вдоль участка ADB совпадает с интегралом вдоль пути АСВ, то сила потенциальна (говорят иначе – поле сил потенциально). Если это не так, то сила относится к числу непотенциальных. Установлено, что потенциальными являются важнейшие фундаментальные силы – гравитационного и электростатического взаимодействия. 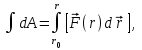 Так как работа, совершенная любой силой, может быть найдена в виде интеграла Так как работа, совершенная любой силой, может быть найдена в виде интегралаа  для случая потенциального поля сил совершенная работа не зависит от формы пути, зависит лишь от начального и конечного положений тела, можно ввести функцию U(r)-функцию координат, определяющую запас потенциальной энергии системы. Тогда совершенная системой работа по перемещению материального тела из точки с координатой для случая потенциального поля сил совершенная работа не зависит от формы пути, зависит лишь от начального и конечного положений тела, можно ввести функцию U(r)-функцию координат, определяющую запас потенциальной энергии системы. Тогда совершенная системой работа по перемещению материального тела из точки с координатой 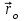 в точку с координатой в точку с координатой 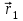 можно найти как разность значений функции U(r), т.е. можно найти как разность значений функции U(r), т.е.A = U(r) = U(r1) – U(ro) = U2 – U1. Эта функция U, зависящая от свойств системы, создающей силовое поле и свойств перемещаемого тела (например, его массы, положения в пространстве и т.п.) – называется потенциальной энергией системы. Работа потенциальной силы всегда равна со знаком минус изменению потенциальной энергии частицы при её перемещении из одного положения в другое. Точный вид функции U зависит от конкретного силового поля и вида взаимодействия. Кулон, с учетом выбора граничных условий, при котором потенциальная энергия системы бесконечно удаленных друг от друга тел равна 0, предложил вид потенциальной функции 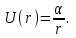 Для важнейших силовых полей мы получим значение коэффициента несколько позже. Для важнейших силовых полей мы получим значение коэффициента несколько позже.Измеряется потенциальная энергия, естественно, в тех же единицах, что и работа, т.е. в джоулях. Связь силы и потенциальной энергии. Каждой точке потенциального поля сил соответствует, с одной стороны, некоторое значение силы F, действующей на тело, с другой стороны – некоторое значение потенциальной энергии U для данной конфигурации взаимодействующих тел. Следовательно, между 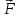 и U должна существовать какая-то функциональная связь. и U должна существовать какая-то функциональная связь.Вычислим элементарную работу dA, совершаемую силами поля при малом перемещении тела 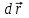 вдоль некоторого произвольного направления S. вдоль некоторого произвольного направления S.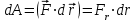 , где Fr = Fcos - проекция силы на направление перемещения. , где Fr = Fcos - проекция силы на направление перемещения.Работа эта совершается за счет запаса потенциальной энергии системы и равна убыли потенциальной энергии (-dU), т.е. dA = - dU(r) или Frdr = -dU. Откуда 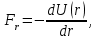 или в векторной форме или в векторной форме 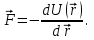 Если отрезок произвольно ориентирован в трехмерном пространстве, то величину силы можно определить параметрически: 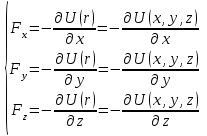 В векторном виде это равенство можно записать еще так 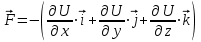 , где , где 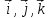 - орты осей координат x,y,z. - орты осей координат x,y,z.В математике вектор 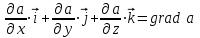 называется градиентом скалярной величины «а». Этот вектор направлен в сторону максимально быстрого увеличения скалярной величины «а». называется градиентом скалярной величины «а». Этот вектор направлен в сторону максимально быстрого увеличения скалярной величины «а».В нашем случае сила (векторная величина) есть градиент потенциальной энергии - величины скалярной. Знак “ – “ указывает, что вектор силы 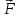 направлен в сторону убывания потенциальной энергии U. направлен в сторону убывания потенциальной энергии U.Иные обозначения 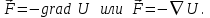 Важное замечание: Прибавление постоянной во времени величины к потенциальной энергии не изменяет картины силового воздействия данного силового поля на данную частицу (тело) (вследствие операции дифференцирования). Следовательно: а) выбор уровня, с которого производится отсчет величины потенциальной энергии – произвольная операция, допускающая удобный выбор; б) строго определенный физический смысл имеет не фиксированное значение потенциальной энергии, а её изменение в данном процессе – приращение или убыль. Графический пример соотношения силы и потенциальной энергии представлен на рис.6.5.     ЗЕМЛЯ ЗЕМЛЯ 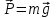 gradU gradUРис.6.5. Связь силы тяжести с потенциальной энергией поля тяготения. Теперь можно рассмотреть величину потенциальной энергии различных физических систем. Кинетическая энергия. Выше подчеркивалось, что механическая работа, которую может совершить физическая система, определяется разностью энергий системы в конечном и начальном состояниях 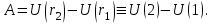 Работа, которую система (тело) может совершить вследствие изменения состояния своего движения, характеризует кинетическую энергию системы (тела). Определяющими параметрами здесь являются скорость и импульс тела. Пусть под действием некоторой силы F тело массой m=const при прямолинейном движении увеличило свою скорость от v1 до v2 (рис.6.8). Сила в общем случае может изменяться от точки к точке, т.е. F = F(S).        F v1 F v2 F v1 F v2 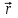  S Рис.6.8. К выводу кинетической энергии. Разбиваем участок S на отрезки dS, достаточно малые, чтобы считать F=const. Тогда 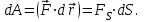 Учитывая Учитывая 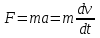 - мгновенное значение силы на отрезке dS, получаем, после замены порядка дифференцирования по однородному параметру S: - мгновенное значение силы на отрезке dS, получаем, после замены порядка дифференцирования по однородному параметру S: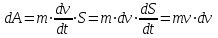 . .Поскольку в начальный момент времени скорость была равна v1, а в конце стала равной v2, то  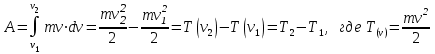 и есть кинетическая энергия тела массой m, движущегося со скоростью v. и есть кинетическая энергия тела массой m, движущегося со скоростью v.Если учесть, что mv=p – импульс тела, то можно получить 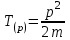 , откуда, кстати, , откуда, кстати, 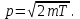   Закон сохранения импульса (вывод) Рассмотрим замкнутую систему из n тел. На каждое из них действуют внутренние силы: 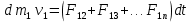 =   = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 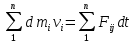 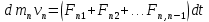 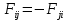  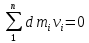  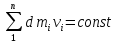 Закон сохранения механической энергии (вывод) Р скалярное умножение ассмотрим незамкнутую систему из n тел. На каждое из них действуют силы: 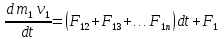 =   = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 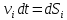 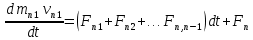 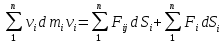   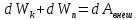 В   замкнутой системе: замкнутой системе: 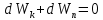 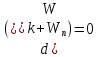 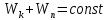     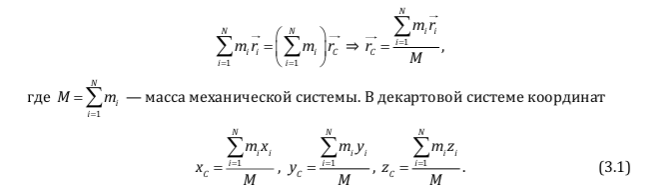 Для выяснения физического смысла центра масс разобьем тело М на N одинаковых частей массой m. Тогда в одномерном случае координата его будет равна: 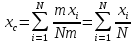 Из последнего следует, что он представляет собой среднеарифметическое координат всех частей тела.   |
