Лекция 1. 1. общие понятия в общем случае волновым процессом

• Название: 1. общие понятия в общем случае волновым процессом
• Анкор: Лекция 1
• Дата: 24.09.2020
• Размер: 0.5 Mb.
• Имя файла: lekciya1n.docx
• Тип: Документы; #139525

1. ОБЩИЕ ПОНЯТИЯ
В общем случае волновым процессом называется любое изменение (возмущение) состояния сплошной среды, распространяющееся с конечной скоростью и несущее энергию.

Существует большое многообразие волновых процессов (типов волн): звуковые волны, сейсмические, волны на поверхности воды, волны механических колебаний в кристаллах, радиоволны, оптические волны. Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за сходства описывающих их физических законов. Законы эти выражаются так называемыми волновыми уравнениями. Для непрерывных систем это обычно дифференциальные уравнения в частных производных. Для материальных сред они часто сводятся к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений.

Выделим два наиболее интересных типа волн: упругие механические и электромагнитные.

Упругие волны (или акустические от греческого слова acustikos – слуховой) – это волны, связанные с колебаниями частиц при механической деформации упругой среды (жидкой, газообразной, твердой). При этом имеет место перенос энергии при отсутствии переноса вещества. В акустической волне частицы совершают колебания вокруг точки покоя. Среди упругих волн самые низкие частоты имеют инфразвуковые волны, лежащие ниже границы слышимости их человеком (ниже 20 Гц). Слышимые звуковые колебания занимают диапазон частот от 20 Гц до 20 кГц. Волны более высоких частот – ультразвуковые (от 20 кГц до 1 ГГц) и гиперзвуковые (от 1 ГГц до 1000 ГГц).

Электромагнитные волны – это распространяющиеся в пространстве переменные во времени электромагнитные поля. Электромагнитные волны всегда имеют поперечные к направлению распространения составляющие векторов напряженностей электрического и магнитного полей. Продольные составляющие этих векторов могут существовать лишь при определенных условиях (у границ раздела разных сред, вблизи возбуждающих источников, в линиях передачи). Чисто продольных электромагнитных волн не существует. Среди электромагнитных волн выделяют радиоволны с диапазоном частот от 3 ⋅10³ Гц до 3 ⋅10¹¹ Гц. Далее по частоте расположен оптический диапазон от 3 ⋅10¹¹ Гц до 3 ⋅10¹⁶ Гц, включающий инфракрасное, видимое и ультрафиолетовое излучения. Колебания более высоких частот - это рентгеновское и гамма – излучения.

Наука, занимающаяся изучением излучения, распространения и поглощения электромагнитных волн, называется электродинамикой.


До диапазона инфракрасных волн все среды можно рассматривать как сплошные без учета их внутренней микроструктуры, волновыми процессами в таких средах занимается классическая электродинамика.

На более высоких частотах следует учитывать микроструктуру среды и дискретность электромагнитного излучения (поток фотонов). В этом случае электромагнитное излучение описывается методами квантовой электродинамики.

Для более подробного ознакомления с механическими колебательными системами рассмотрим следующие примеры.

1. Поместим на поверхности воды в сосуде легкий поплавок. Осторожно добавим еще один. Появление второго поплавка никак не отражается на первом, и можно считать, что поплавки не взаимодействуют. Легкими нажатиями заставим один поплавок совершать колебания на поверхности воды. На этот раз механическое состояние второго поплавка не останется неизменным. Через некоторое время он также начнет колебаться. При этом можно заметить, что от первого поплавка, которому мы принудительно придали колебательное движение, по поверхности воды «пошли круги». В повседневной жизни такие круги называют волнами.

2. Возьмем длинный шнур и закрепим один из его концов. Другой конец, встряхнув его, приведем в колебательное движение. При этом мы увидим, что вдоль шнура что-то «бежит», хотя концы шнура останутся на месте. То, что «бежит» по шнуру, тоже называют «волной».

Существуют еще множество явлений аналогичного характера, в основе которых лежит одна и та же физическая природа и которые объединены общим названием – волновые процессы.

Что же представляют собой волны?

Если колеблющееся тело (струна, камертон, мембрана громкоговорителя) находится в упругой среде, то оно приводит в колебательное движение соприкасающиеся с ним частицы среды, вследствие чего в прилегающих к этому телу элементах среды возникают периодические деформации (например, сжатия и растяжения). При этих растяжениях в среде появляются упругие силы, стремящиеся вернуть элементы среды к первоначальным состояниям равновесия. Благодаря взаимодействию соседних элементов среды, упругие деформации будут передаваться от одних участков среды к другим, более удаленным от колеблющегося тела. Таким образом, периодические возмущения (возбуждения), которые имеют место в каком-либо месте упругой среды, не остаются локализованными в этом месте, а распространяются в среде с некоторой скоростью, зависящей от ее физических свойств. При этом частицы среды совершают колебательные движения около их положений равновесия; от одних участков среды к другим передается только состояние деформаций – процесс распространения упругих волн не сопровождается поступательным перемещением вещества, а является лишь одним из механизмов передачи энергии от источника волн к частицам, составляющим упругую среду.

Из вышесказанного следует, что механические волны возникают благодаря вынужденному движению некоторой части деформируемой среды. Возмущение, вызвавшее деформацию, передается от одной точки к другой, т.е. механическая волна распространяется внутри некоторой среды. При этом существует сопротивление среды, которое противодействует деформации так же, как при обычном механическом движении существует сопротивление движению из-за инертности движущегося тела, которое необходимо преодолеть.

Итак, с физической точки зрения упругость и инертность среды являются необходимыми и важнейшими свойствами ее для того чтобы в ней распространялись волны. Действительно, опыты показывают, что скорость распространения волн всегда выражается как функция квадратного корня параметра, характеризующего сопротивление среды деформации, и параметра, который определяет ее инертность.

Например, для звука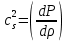

,

где c_s – скорость звука, Р – звуковое давление, ρ – плотность среды, в которой распространяется звук.

Если бы среда не была деформируемой (абсолютно твердое тело), локальное возмущение в какой-либо точке просто передалось бы в другую точку в форме силы или ускорения. Если бы среда была лишена инертности, не существовало бы запаздывания при перемещении частиц, и передача возмущения от одной частицы к другой во всей среде происходила бы мгновенно. На самом деле все среды являются деформируемыми и обладают массой (инертностью) так что во всех средах могут существовать механические волны.

В зависимости от характера возникающих при этом деформаций различают волны продольные и поперечные. В продольных волнах частицы среды колеблются вдоль линии, совпадающей с направлением распространения волны (рис. 1.2).




В поперечных волнах частицы среды колеблются перпендикулярно направлению распространения волны (рис. 1.3).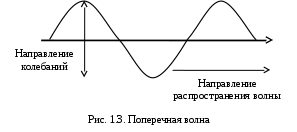


Упругие поперечные волны могут возникать лишь в среде, обладающей сопротивлением деформации сдвига. Газообразные и жидкие среды не имеют упругости сдвига, и поэтому в них возбуждаются только продольные волны, распространяющиеся в виде чередующихся сжатий и разрежений среды. В твердых телах могут существовать и продольные и поперечные волны.

Рассмотрим процесс образования поперечных волн. Возьмем в качестве модели реального шнура цепочку шариков (материальных точек), связанных друг с другом упругими силами. На рис. 1.4 изображен процесс распространения поперечной волны и показаны положения шариков через последовательные промежутки времени, равные четверти периода.

В начальный момент времени (t₀ = 0) все точки находятся в состоянии равновесия (рис. 1.4, а). Затем вызываем возмущение, отклонив точку 1 от положения равновесия на величину А и 1-я точка начинает колебаться, 2-я точка, упруго связанная с 1-й, приходит в колебательное движение несколько позже, 3-я — еще позже и т.д. Через четверть периода колебания (t₂ = T/4 )  распространятся до 4-й точки, 1-я точка успеет отклониться от своего положения равновесия на максимальное расстояние, равное амплитуде колебаний А (рис. 1.4, б). Через полпериода 1-я точка, двигаясь вниз, возвратится в положение равновесия, 4-я отклонилась от положения равновесия на расстояние, равное амплитуде колебаний А (рис. 1.4, в), волна распространилась до 7-й точки и т.д.

К моменту времени t₅ = T 1-я точка, совершив полное колебание, проходит через положение равновесия, а колебательное движение распространится до 13-й точки (рис. 1.4, д). Все точки от 1-й до 13-й расположены так, что образуют полную волну, состоящую из впадины и горба.



Продольную волну можно наблюдать на длинной мягкой пружине большого диаметра. Ударив по одному из концов пружины, можно заметить, как по пружине будут распространяться последовательные сгущения и разрежения ее витков, бегущие друг за другом. Цепочка при этом остается прямой. На рис. 1.5 точками показано положение витков пружины в состоянии покоя, а затем положения витков пружины через последовательные промежутки времени, равные одной четверти периода.


Таким образом, продольная волна в рассматриваемом случае представляет собой чередующиеся сгущения (Сг) и разрежения (Раз) витков пружины.

В рассмотренных выше примерах показаны колебания частиц, положения равновесия которых лежат на горизонтальной оси. В реальных условиях колеблются не только частицы, расположенные вдоль некоторой горизонтальной оси, а совокупность частиц, заключенных в некотором объеме. Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые частицы пространства. Геометрическое место точек, до которых доходят колебания к некоторому моменту времени t, называется фронтом волны. Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникали. Форма фронта волны определяется конфигурацией источника колебаний и свойствами среды.

В однородных средах скорость распространения волны везде одинакова. Среда называется изотропной, если эта скорость одинакова по всем направлениям. Фронт волны от точечного источника колебаний в однородной и изотропной среде имеет вид сферы. Такие волны называются сферическими. В неоднородной и анизотропной среде, а также при неточечных источниках колебаний фронт волны имеет сложную форму.

При описании волновых процессов в среде выделяют поверхности, в которых все частицы колеблются в одинаковой фазе. Эти поверхности одинаковой фазы называются волновыми, или фазовыми. Они также могут быть сферическими, плоскими или иметь сложную форму в зависимости от формы источника колебаний и свойств среды. На рис. 1.6 показаны:

а) сферическая волна от точечного источника;

б) волна от колеблющейся пластинки;

в) эллиптическая волна от точечного источника в анизотропной среде, в которой скорость распространения волны плавно меняется по мере изменения угла φ, достигая максимума вдоль направления АА и минимума – вдоль направления ВВ. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается.





Рассмотрим случай, когда плоская волна распространяется вдоль оси Ох. Тогда все точки среды, положения равновесия которых имеют одинаковую координату х (но различные значения координат y и z), колеблются в одинаковой фазе (точки, лежащие в плоскости x = const) (рис. 1.7).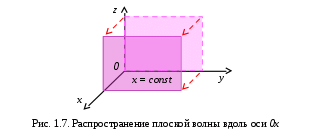



На рис. 1.8 изображена кривая, которая иллюстрирует смещение u точек с различными х из положения равновесия в некоторый момент времени (синусоидальная волна). Кривая отображает график функции u(x,t) для некоторого фиксированного момента времени. С течением времени такая волна в однородной и изотропной среде смещается, сохраняя свою форму (пунктирная синусоида).

Обратимся опять к рис. 1.4. Допустим, что к тому моменту времени, когда точка 1 пройдет путь от положения равновесия до крайнего верхнего положения (на это уйдет четверть периода колебаний точки 1), успеют начать колебаться точки 2 и 3. Точки правее третьей еще покоятся. До них не дошла «очередь». К моменту, когда точка 1 вернется в положение равновесия (вариант на рис. 1.4, соответствующий моменту времени t= T/2), начнут свои колебания точки 4-6 и т.д.).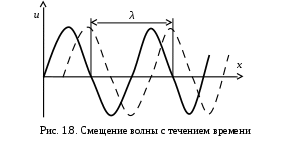




Через промежуток времени, равный периоду колебаний шариков, шарик 1 завершит свое первое колебание. К этому времени соседняя точка 2 этого сделать не успеет, поскольку она начала двигаться позднее. Она и закончит свое первое колебание позже точки 1. Еще позднее это сделают точки 3, 4, 5 и т.д.

На некотором расстоянии от точки 1 находится точка, которая опаздывает с началом колебаний ровно на один период (точка 13). Это значит, что за время, равное одному периоду колебания Т, колебание успело распространиться до точки 13. Эта точка начнет свое первое колебание, когда точка 1 начнет свое второе колебание. Обозначим расстояние, на которое колебание распространяется за время Т, греческой буквой λ. Называется оно длиной волны. Ясно, что точка, расположенная на расстоянии 2λ от точки 1, начнет свое первое колебание в тот момент, когда точка 1 начнет свое третье колебание, а точка 13 – второе. Эти точки, следовательно, движутся одинаково: они одновременно начинают двигаться вверх, вместе проходят положение равновесия, одновременно движутся вниз, одновременно заканчивают очередное колебание и начинают следующее. И не только они, но и любые точки, отстоящие одна от другой на расстояниях λ, 2λ, 3λ и т.д. Можно поэтому сказать, что длина волны равна расстоянию между двумя ближайшими точками, движущимися одинаково и имеющими одинаковые отклонения от положения равновесия (рис. 1.4 и рис. 1.8).

Таким образом, мы имеем два эквивалентных определения длины волны:

а) длина волны – это расстояние между ближайшими точками среды, колеблющимися с разностью фаз 2π;

б) длина волны – это расстояние λ, на которое распространяется волна за время, равное периоду колебаний частиц среды.

Очевидно, что

λ = cT, (1.1)
где с – скорость распространения волны, Т – период колебаний.

Эти два с первого взгляда разных определения длины волны позволяют уточнить физический смысл скорости с, введенной в формуле (1.1). С одной стороны, это скорость, с которой перемещается возмущение (фронт волны) в среде. С другой стороны, из определения волновой поверхности следует, что фаза волны в заданной точке среды меняется со временем, а в заданный момент времени является функцией координат. Если задать какое-либо определенное значение фазы, то с течением времени оно будет достигаться то в одной, то в другой точке среды. Поэтому можно говорить о перемещении фазы. Скорость этого перемещения называется фазовой скоростью и совпадает со скоростью распространения волны, поскольку за период Т мы найдем точку среды, имеющую то же значение фазы колебаний, а из предыдущих рассуждений следует, что она отстоит от первой точки на расстояние λ. Несколько позже мы получим математическое обоснование этого утверждения, где первоначально введенная скорость распространения (рис. 1.7) совпадает с определением фазовой скорости волны с.

Часто Т называют временным периодом волны, а λ - пространственным периодом волны.

Заменив в соотношении (1.1) Т – величиной 1/ν (ν - частота колебаний), получим

λ = с/ν. (1.2)
2. УРАВНЕНИЯ ПЛОСКОЙ И СФЕРИЧЕСКОЙ ВОЛН
При описании волнового процесса требуется найти амплитуды и фазы колебательного движения в различных точках среды и изменение этих величин с течением времени. Эта задача может быть решена в том случае, если известно, по какому закону колеблется и как взаимодействует со средой тело, вызвавшее волновой процесс. Однако во многих случаях не существенно, каким телом возбуждена данная волна, а решается более простая задача. Задано состояние колебательного движения в некоторых точках среды в определенный момент времени и требуется определить состояние колебательного движения в других точках среды.

Для примера рассмотрим решение такой задачи в простом, но вместе с тем важным случае распространения в среде плоской или сферической гармонической волны. Обозначим колеблющуюся величину через u. Этой величиной могут быть: смещение частиц среды относительно их положения равновесия, отклонения давления в данном месте среды от равновесного значения и т.д. Тогда задача будет состоять в отыскании так называемого уравнения волны – выражения, которое задает колеблющуюся величину u как функцию координат точек среды x, y, z и времени t:

u = u(x, y, z, t). (2.1)

Пусть для простоты u – это смещение точек в упругой среде, когда в ней распространяется плоская волна, а колебания точек имеют гармонический характер. Кроме того, направим оси координат так, чтобы ось 0х совпала с направлением распространения волны. Тогда волновые поверхности (семейство плоскостей) будут перпендикулярными к оси 0х (рис. 1.7), и поскольку все точки волновой поверхности колеблются одинаково, смещение u будет зависеть только от х и t: u = u(x, t). Для гармонических колебаний точек, лежащих в плоскости х = 0 (рис. 1.9), справедливо уравнение:

u(0, t) = A cos (ωt + α) (2.2)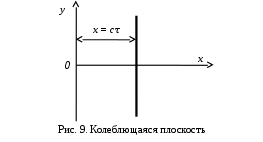




Найдем вид колебаний точек плоскости, соответствующей произвольному значению х. Для того чтобы пройти путь от плоскости х = 0 до этой плоскости, волне требуется время τ = х/с (с – скорость распространения волны). Следовательно, колебания частиц, лежащих в плоскости х, будут иметь вид:



Итак, уравнение плоской волны (и продольной, и поперечной), распространяющейся в направлении оси 0х, выглядит следующим образом: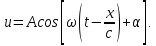

(2.3)

Величина А представляет собой амплитуду волны. Начальная фаза волны α определяется выбором начала отсчета х и t.

Зафиксируем какое-либо значение фазы, стоящей в квадратных скобках уравнения (2.3), положив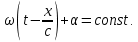

(2.4)

Продифференцируем это равенство по времени с учетом того, что циклическая частота ω и начальная фаза α являются постоянными: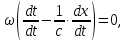



откуда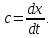

(2.5)

Таким образом, скорость распространения волны с в уравнении (2.3) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью. В соответствии с (2.5) dx/dt > 0. Следовательно, уравнение (2.3) описывает волну, распространяющуюся в направлении возрастания х, так называемую бегущую прогрессивную волну. Волна, распространяющаяся в противоположном направлении, описывается уравнением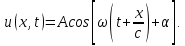

(2.6)

и называется бегущей регрессивной волной. Действительно, приравняв константе фазу волны (2.6) и продифференцировав получившееся равенство, придем к соотношению: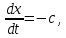



из которого следует, что волна (2.6) распространяется в сторону убывания значений х.

Введем величину

(2.7)

которая называется волновым числом и равна количеству длин волн, укладывающихся на интервале 2π метров. С помощью формул λ = с/ν и ω = 2πν волновое число можно представить в виде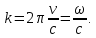

(2.8)

Раскрыв скобки в формулах (2.3) и (2.6) и приняв во внимание (2.8), придем к следующему уравнению плоских волн, распространяющихся вдоль (знак «–») и против (знак «+») оси 0х: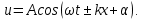

(2.9)

При выводе формул (2.3) и (2.6) предполагалось, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. Опыт показывает, что в поглощающей среде интенсивность волны по мере удаления от источника колебаний постепенно уменьшается – наблюдается затухание волны по экспоненциальному закону: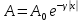

.

Соответственно, уравнение плоской затухающей волны имеет вид: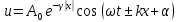

(2.10)

где A₀ – амплитуда в точках плоскости х = 0, а γ – коэффициент затухания.

Теперь найдем уравнение сферической волны. Всякий реальный источник волн обладает некоторой протяженностью. Однако если ограничиться рассмотрением волны на расстояниях от источника, много больших его размеров, то источник можно считать точечным. В изотропной и однородной среде волна, порождаемая точечным источником, будет сферической. Допустим, что фаза колебаний источника ωt+α. Тогда точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой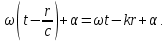



Амплитуда колебаний в этом случае, даже если энергия волны не поглощается средой, постоянной не останется – она убывает в зависимости от расстояния от источника по закону 1/r. Следовательно, уравнение сферической волны имеет вид: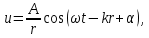

(2.11)

где А – постоянная величина, численно равная амплитуде колебаний на расстоянии от источника, равном единице.

Для поглощающей среды в (2.11) нужно добавить множитель e^-γr. Напомним, что в силу сделанных предположений уравнение (2.11) справедливо только для r, значительно превышающих размеры источника колебаний. При стремлении r к нулю амплитуда обращается в бесконечность. Этот абсурдный результат объясняется неприменимостью уравнения (2.11) для малых r.