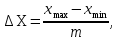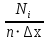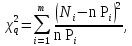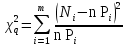Приклалная. 1 Изучение конструкции средства измерения. 1 Изучение конструкции средства измерения
 Скачать 377.89 Kb. Скачать 377.89 Kb.
|
|
2.2 Исключение грубых погрешностей Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдений хi не содержит грубой погрешности, то есть является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть вдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность, и его исключают. Границы цензурирования tгp ∙Sx выборки зависят не только от объема n, но и от вида распределения. Назначая ту или иную границу, необходимо оценить уровень значимости q=1 - P, то есть вероятность исключения какой-либо части отсчетов, принадлежащих обрабатываемой выборке. Для более точных расчетов границ цензурирования прямоугольного распределения используют выражение 2.14:
После определения параметра tгр =2,16 для вероятности Р=0,95 верхняя и нижняя граница предельных значений отсчетов определяют выражениями 2.15: 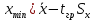 , ,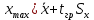 (2.15) (2.15)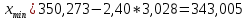 , ,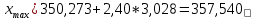 . .В полученный интервал входят все значения. 2.3 Определение закона распределения вероятности результатов измерений Определив оценки основных начальных и центральных моментов и показателей формы, можно предварительно оценить характер кривой плотности распределения вероятности. Так как |A|1,5A , то распределение можно считать симметричным. О наличие моды можно судить только после построения гистограммы. По значения Е и 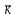 как говорилось уже ранее можно предполагать, что ЗВР прямоугольный. как говорилось уже ранее можно предполагать, что ЗВР прямоугольный.2.3.1 Построение гистограммы Для уточнения формы ЗВР прибегают к построению гистограммы. Гистограмма представляет собой ступенчатый график, состоящий из прямоугольников, у которых основаниями служат частные интервалы ΔXi на оси абсцисс, а площади равны частотам вариантов, попадающих в эти интервалы. Для построения гистограммы необходимо выбрать оптимальное число интервалов группирования экстремальных данных. Необходимость оптимизации числа интервалов связана, в первую очередь, с требованием построения гистограммы, наиболее близкой к действительной кривой плотности распределения вероятности, и исключения промахов при определении закона распределения вероятности экспериментальных данных. Для количества значений от 40 до 100 выбираем количество интервалов равное 9. Определить длину интервала ΔX по формуле (2.20):
где m – число интервалов гистограммы. 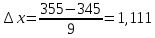 Наименьшее граничное значение для первого интервала будет равно xmin. Найти вторую границу интервала, прибавляя ΔX. Составить таблицу для подсчета частот соответствующих интервалов. Определить количество значений, попавших в каждый интервал, и подсчитать частоты. Построить гистограмму распределения, нанося по оси абсцисс границы интервалов, а по оси ординат – шкалу для частот. Для каждого класса строят прямоугольник с основанием, равным ширине интервала, и с высотой, соответствующей частоте попадания данных в этот интервал, определяемой по отношению 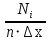 . В таблице 2.2 проведен подсчет частот интервалов гистограммы. . В таблице 2.2 проведен подсчет частот интервалов гистограммы.Таблица 2.2 – Подсчет частоты интервалов гистограммы
На рисунке 2.1 представлен вид полученной гистограммы. 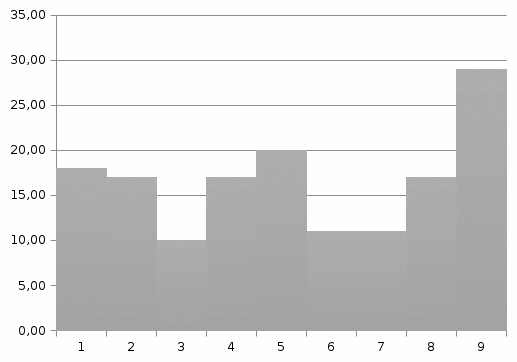 Рисунок 2.1 – Гистограмма построенная по данным таблицы 2.3 Далее по полученной гистограмме строится полигон. Построение осуществляется путем соединения середин верхних оснований каждого столбца гистограммы прямыми. Полигон распределения изображен на рисунке 2.2. 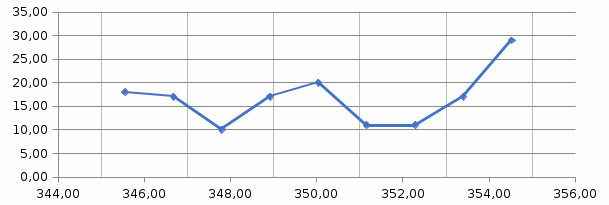 Рисунок 2.2 – Полигон распределения 2.3.2 Аппроксимация гистограммы и полигона распределения аналитической функцией плотности вероятности Случайная величина не имеет более полного описания, чем аналитическая кривая плотности распределения. Поэтому идентификация формы распределения сводится к выбору аналитической модели, которая не противоречит данной выборке экспериментальных данных. Предполагаем, что функция плотности распределения вероятности близка к равномерной. Значение экспериментальной плотности вероятности Рэкс(х) попадания отсчетов в m интервал в зависимости от х определяются величиной 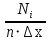 . Полученные результаты относят к середине интервала. . Полученные результаты относят к середине интервала.Значения теоретической плотности распределения вероятности Ртеор(х) получаются по теоретической зависимости ,которая должна быть близка по форме к экспериментально полученному полигону и описывается аппроксимирующим аналитическим выражением. Представим аналитическое выражение аппроксимирующей функции в следующем виде: 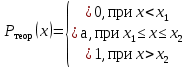 Параметр а определим как среднее арифметическое экспериментального полигона распределения вероятности в серединах интервалов. Эта величина приблизительно равна а=2,097. Проверку правильности расчетов целесообразно провести исходя их двух условий: среднее арифметическое значение экспериментальной и аппроксимирующей кривых должны быть равны; площадь под аппроксимирующей кривой должна быть близка к единице. Значение теоретической и экспериментальной плотности распределения вероятности записаны в таблице 2.3 и представлены на рисунке 2.3. Таблица 2.3 – Значение теоретической и экспериментальной плотности распределения вероятности
Таким образом, первое и второе условие выполняются, следовательно, в качестве аппроксимирующей функции можно принять рассмотренное аналитическое выражение. 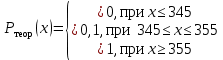 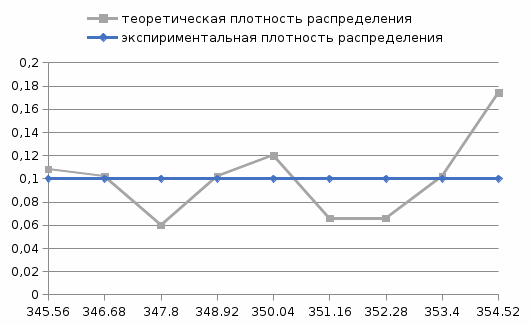 Рисунок 2.3 – Значение теоретической и экспериментальной плотности распределения вероятности 2.3.3 Использование критериев согласия при идентификации формы распределения результатов измерения В качестве способа оценки близости распределения выборки экспериментальных данных к принятой аналитической модели закона распределения обычно рекомендуется использование так называемых критериев согласия. Критерии согласия позволяют оценить вероятность того, что полученная выборка не противоречит сделанному предположению о виде закона распределения рассматриваемой случайной величины. Для этого выбирается некоторая величина u, являющаяся мерой расхождения статистического и теоретического законов распределения, и определяется такое ее значение u, чтобы P(uu) =, где – достаточно малая величина (уровень значимости), значение которой устанавливается в соответствии с существом задачи. Если значение меры расхождения uq полученное на опыте, больше u, то отклонение от теоретического закона распределения считается значимым и предположение о виде закона распределения должно быть отвергнуто. Если значение uq u, то отклонение считается не значимым, то есть данные опыта не противоречат сделанному предположению о виде закона распределения. В различных критериях согласия в качестве меры расхождения статистического и теоретического законов распределения принимаются различные величины. В критерии согласия К. Пирсона (критерий 2) за меру расхождения принимается величина 2, опытное (расчетное) значение 2q, которое определяется оп формуле (2.22):
где m – число сравниваемых частот; Ni – частота (количество отсчетов, попавших в i-ый интервал); n – количество отсчетов в исходном массиве результатов измерений; Рi – вероятность попадания случайной величины х в i-ый интервал. При n закон распределения 2q независимо от вида закона распределения случайной величины х стремится к закону 2 – распределения с k=m-r-1 степеней свободы, где r – число параметров теоретического закона распределения, вычисляемых по данной выборке (r=2 для нормального и равномерного распределения). Проверим гипотезу о принадлежности результатов измерения к равномерному распределения по критерию К. Пирсона. Так как рассматриваемый вид распределения равномерный, то формуле для подсчета критерия Pi будет равно рассчитанной ранее величине Ртеор(х)*Δх. В таблице 2.4 приведены некоторые необходимые расчеты. Таблица 2.4 – Данные для расчета критерия К. Пирсона
Теперь полученные значения в шестом столбце таблицы 2.5 суммируем по формуле (2.23).
Полученное рассчитанное значение 2q сравниваем с табличным при k=6 и P=0,95, которое равно 2=12,592. 2q 2, значит не принимается гипотеза о том, что результат измерения подчиняется равномерному закону распределения. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

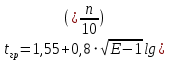 =2,40
=2,40