Лекция по математике. Тема__Комплексные числа и действия с ними_. 1. Введение понятия комплексного числа

• Название: 1. Введение понятия комплексного числа
• Дата: 21.12.2022
• Размер: 36.03 Kb.
• Имя файла: Лекция по математике. Тема__Комплексные числа и действия с ними_.docx
• Тип: Лекция; #856184

Лекция

Комплексные числа и действия с ними

План

1. Введение понятия комплексного числа.

2.Алгебраична форма комплексного числа.

3. Действия над комплексными числами в алгебраической форме.

1. Введение понятия комплексного числа.

Как известно, имеются различные числовые системы: натуральных, целых, рациональных, действительных чисел. Каждая из этих числовых систем моделирует определенные типы количественных отношений действительного мира, другими словами, предназначена для решения определенного вида задач. Исторически почти одновременно возникли понятия натурального и положительного рационального (дробного) чисел. При помощи натуральных чисел решаются произвольные задачи, связанные с определением количества элементов любого конечного множества, т. е. решается любая задача счета. В множестве рациональных чисел решаются любые задачи, связанные с операцией деления, которые, как легко видеть, в множестве натуральных чисел не всегда имеют решения. Намного позже люди пришли к понятию отрицательного числа. Необходимость введения этого понятия связана с моделированием процессов, величин, которые меняются в двух противоположных направлениях. Примерами таких величин являются температура, уровень реки, прибыль, скорость прямолинейного движения некоторого тела.

Таким образом, на каждом этапе необходимость расширения понятия числа связана с тем, что в имеющемся множестве чисел не всегда решаются отдельные важные задачи, т. е. не всегда выполнимы некоторые операции и новые числа вводятся так, чтобы рассматриваемые операции стали выполнимыми.

Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i – мнимая единица, причем i² = - 1.

Исходя из этого, получим следующее определение комплексного числа.

Определение. Комплексным числом называется выражение вида a + bi, гдеaи b - действительные числа. При этом выполняются условия:

а) Два комплексных числа a₁ + b₁iи a₂ + b₂iравны тогда и только тогда, когда a₁=a₂, b₁=b₂.

б) Сложение комплексных чисел определяется правилом:

(a₁ + b₁i) + (a₂ + b₂i) = (a₁ + a₂) + (b₁ + b₂) i.

в) Умножение комплексных чисел определяется правилом:

(a₁ + b₁i) (a₂ + b₂i) = (a₁a₂ - b₁b₂) + (a₁b₂ - a₂b₁) i.

2. Алгебраическая форма комплексного числа.

Запись комплексного числа в виде a + biназывают алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.

Комплексное число a + biсчитается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0

Комплексное число a + biпри b = 0 считается совпадающим с действительным числом a: a + 0i = a.

Комплексное число a + biпри a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.

Два комплексных числа z = a + bi и 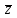= a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

3.Действия над комплексными числами в алгебраической форме.

Над комплексными числами в алгебраической форме можно выполнять следующие действия.

1) Сложение.

Определение. Суммой комплексных чисел z₁ = a₁ + b₁i и z₂ = a₂ + b₂iназывается комплексное число z, действительная часть которого равна сумме действительных частей z₁ и z₂, а мнимая часть - сумме мнимых частей чисел z₁ и z₂, то есть z = (a₁ + a₂) + (b₁ + b₂)i.

Числа z₁ и z₂ называются слагаемыми.

Сложение комплексных чисел обладает следующими свойствами:

1º. Коммутативность: z₁ + z₂ = z₂ + z₁.

2º. Ассоциативность: (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃).

3º. Комплексное число –a –bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0

Пример 1. Выполните сложение (3 – i) + (-1 + 2i).

(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Вычитание.

Определение. Вычесть из комплексного числа z₁ комплексное число z₂, значит найти такое комплексное число z, что z + z₂ = z₁.

Теорема. Разность комплексных чисел существует и притом единственна.

Пример 2. Выполните вычитание (4 – 2i) - (-3 + 2i).

(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.

3) Умножение.

Определение. Произведением комплексных чисел z₁=a₁+b₁i и z₂=a₂+b₂i называется комплексное число z, определяемое равенством: z = (a₁a₂ – b₁b₂) + (a₁b₂ + a₂b₁)i.

Числа z₁ и z₂ называются сомножителями.

Умножение комплексных чисел обладает следующими свойствами:

1º. Коммутативность: z₁z₂ = z₂z₁.

2º. Ассоциативность: (z₁z₂)z₃ = z₁(z₂z₃)

3º. Дистрибутивность умножения относительно сложения:

(z₁ + z₂) z₃ = z₁z₃ + z₂z₃.

4º. z · 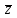= (a + bi)(a – bi) = a² + b² - действительное число.

На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.

В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.

Пример 3. Выполните умножение (2 + 3i) (5 – 7i).

1 способ. (2 + 3i) (5 – 7i) = (2 5 – 3 (- 7)) + (2 (- 7) + 3 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i.

2 способ. (2 + 3i) (5 – 7i) = 2 5 + 2 (- 7i) + 3i 5 + 3i (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.
4) Деление.

Определение. Разделить комплексное число z₁ на комплексное число z₂, значит найти такое комплексное число z, что z · z₂ = z₁.

Теорема. Частное комплексных чисел существует и единственно, если z₂ ≠ 0 + 0i.

На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.

Пусть z₁ = a₁ + b₁i, z₂ = a₂ + b₂i, тогда .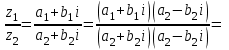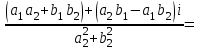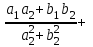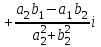

В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.

Пример 4. Найти частное .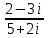

1 способ.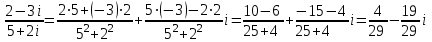

.
2 способ.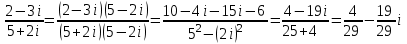

.

5) Возведение в целую положительную степень.

а) Степени мнимой единицы.

Пользуясь равенством i² = -1, легко определить любую целую положительную степень мнимой единицы. Имеем:

i³ = i² i = -i,

i⁴ = i² i² = 1,

i⁵ = i⁴ i = i,

i⁶ = i⁴ i² = -1,

i⁷ = i⁵ i² = -i,

i⁸ = i⁶ i² = 1 и т. д.

Это показывает, что значения степени iⁿ, где n – целое положительное число, периодически повторяется при увеличении показателя на 4 .

Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.

Пример 5. Вычислите: (i ³⁶ + i ¹⁷) · i ²³.

i ³⁶ = (i ⁴)⁹ = 1⁹ = 1,

i ¹⁷ = i ^{4 4+1} = (i ⁴)⁴ i = 1 · i = i.

i ²³ = i ^{4 5+3} = (i ⁴)⁵ i³ = 1 · i³ = - i.

(i³⁶ + i¹⁷) · i²³ = (1 + i) (- i) = - i + 1= 1 – i.

б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.

Пример 6. Вычислите: (4 + 2i)³

(4 + 2i)³ = 4³ + 3 4² 2i + 3 4 (2i)² + (2i)³ = 64 + 96i – 48 – 8i = 16 + 88i.

Упражнения

1.Выполнить сложение комплексних чисел:

1. 
   (3+2ί) + (-1-5ί) = (3-1) + (2-5)ί = 2-3ί
   
2. 
   (4-5ί) + (2-ί) = (4+2) + (-5-1)ί = 6-6ί
   
3. 
   (2+3ί) + (6-3ί) = (2+6) + (3-3)ί= 8
   
4. 
   (10 – 3ί) + (-10+3ί) = (10-10) + (-3+3)ί = 0
   

2.Выполнить вычитание комплексних чисел.

1. 
   (3+4ί) – (1+2ί) = (3-1) + (4-2)ί = 2 + 2ί;
   
2. 
   (-5+2ί) – (2+ί) = (-5-2) + (2-1)ί = -7+ί;
   
3. 
   (6+7ί) – (6-5ί) = (6-6) + (7+5)ί = 12ί;
   
4. 
   (0,3+2,5ί) – (-0,75+1,5ί) = (0,3+0,75ί) + (2,5-1,5ί) = 1,05+ί;
   
5. 
   (2-2ί) – (2+3ί) = (2-2) + (-2-3)ί = -5ί;
   
6. 
   1+1/2) – (1/4-3/5) = (1/3-1/4) + (1/2+3/5) = 1/12 + 11/10.
   

3. Выполнить умножение комплексних чисел.

1. 
   1) (4-5ί)(3+2ί) = 12+8ί -15ί -10ί²= 12+10-7ί =22-7ί;
   

2)(3-ί)(2+5ί) = 6-2ί+15ί-5 ί²= (6+5) + (15-2)ί;

3)8ίх3ίх3 = -243; 4)(2-ί)(-5) = -10+5ί; 5)(-4-3ί)(-6ί) = -18+24ί.

4. Найти произведение комплексних чисел.

1. 
   (3+5ί)(3-5ί) = 9+25 = 34;
   
2. 
   (2+ί)(2-ί) = 4+1 = 5;
   
3. 
   (4+3ί)(4-3ί) = 16+3 = 19;
   
4. 
   (х+уί)( х-уί) = х+у;
   
5. 
   (3/4+2/5ί)(3/4-2/5ί) = 9/16+4/25 = 289/400.
   

5. Разложить на множители двучлен

1)а+9 = (а+3ί)(а-3ί);

2)16m²+25n² = (4m+5nί)(4m-5nί);

3)49+36 = (7+6ί)(7-6ί);

4)а+16 = (а+4ί)( а-4ί);

5)в+7 = (в+7ί)( в-7ί).

6. Найти частное комплексних чисел.

1) (2+5ί)/(3-2ί) = (2+5ί)(3+2ί)/(3-2ί)(3+2ί) = (-4+19ί)/13 = -4/13+19ί/13;

2) (3+ί)/ί = (3+ί)(-ί)/ί = 1-3ί;

7. Возвести в степень двучлени:

1. 
   (2+5ί)² = 4+20ί +25ί² = -21+20ί;
   
2. 
   (3+2)³ = 27+54ί +36ί²+8 = -9+36ί;
   
3. 
   (1+ί)² = 1+2ί + ί²= 2ί;
   
4. 
   (1-ί) ² = 1-2ί + ί²= -2ί;
   
5. 
   (1-ί) = (1-2ί +ί) ² = (-2ί) ² = 4ί² = -4;
   
6. 
   (1+ί) = ((1+ί)²)³ = (2ί) ³ = 8ί³ = -8 ί;
   

Вопросы для самопроверки:

1. Имеет уравнение 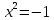решение на множестве комплексных чисел?

2.Что називается комплексним числом?

3. Назовите мнимую и действительную части комплексного числа и какими символами их обозначают?

4. В каком случае комплексное число совпадает с действительным числом?

5. В каком случае комплексное число называется чисто мнимым?

6. Имеет смысл понятия «больше» и «меньше» для комплексных чисел?

7.Какие комплексные числа называются сопряженными?

8.Что называется суммой двух комплексных чисел?

9.Какие комплексные числа называют противоположными?

10.Что называется разностью двух комплексных чисел?

11. Что называется произведением двух комплексных чисел?

12.Что называется частным двух комплексных чисел?