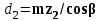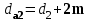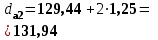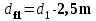Кинематический расчет червячной передачи. кинематический расчет и расчет передачи. 1 Кинематическая схема машинного агрегата. Срок службы приводного устройства
 Скачать 218.47 Kb. Скачать 218.47 Kb.
|
|
1 Кинематическая схема машинного агрегата. Срок службы приводного устройства 1.1 Чертёж кинематической схемы  1 – двигатель; 2 – муфта; 3 –шестерня; 4 –вал быстроходный; 5 – колесо зубчатое; 6 – вал тихоходный;7 – подшипник Рисунок 1 – Кинематическая схема привода 1.2 Условия эксплуатация приводного устройства Привод предназначен для получения вращающего момента на ведомом валу за счет уменьшения его угловой скорости Таблица 1.1 – Исходные данные
1.3 Определяем срок службы приводного устройства Lh , ч Lh=365∙Ln∙tc∙Lc∙0,85 , (1.1) где Lh - срок службы приводного устройства; Lr - срок службы привода, лет; tc - продолжительность смены, ч; Lс - число смен в сутки; Lh=365∙5∙8∙1∙0,85=12410 Рабочий ресурс привода принимаем Lh =12500ч 2 Выбор двигателя. Кинематический и силовой расчеты привода Двигатель является одним из основных элементов машинного агрегата. Для проектируемого привода рекомендуются трёхфазные короткозамкнутые двигатели серии 4А. Эти двигатели наиболее универсальны. Закрытое и обдуваемое исполнение позволяет применять эти двигатели для работы в закрытых условиях, в открытых помещениях и т.д. 2.1 Определение мощности и частоты вращения двигателя Мощность двигателя зависит от требуемой мощности рабочей машины, а его частота вращения –отчастотывращенияприводноговаларабочеймашины. 2.1.1 Определяем мощность и частоты вращения двигателя, Рдв, кВт Рдв= Рт / 𝜂 , (2.1) где Рт–мощностьнатихоходномвалу, кВт; η–общийКПДпривода; ηм= 0,98 –КПДмуфты; ηзуб=0,96…0,97 –КПДзакрытойцилиндрической зубчатой передачи. Принимаем ηзуб= 0,96; ηn= 0,99 –КПД одной пары подшипников качения; 𝜂=0,98∙0,96∙0,99 2=0,92 Рдв=2,6/0,92=2,8 кВт 2.1.2 Определяем номинальную мощность двигателя Рном , кВт Значение номинальной мощности выбираем из таблицы 2.1 по величине большей, но ближайшей к требуемой мощности Рдв Рном ≥Рд,, (2.2) Рном=3кВТ > Рдв=2,8кВТ 2.1.3 Выбор типа двигателя По таблице К1 [1] выбираем двигатель серии 4А с номинальной мощностью Рном=3кВТ, принимаем для расчета четыре варианта двигателей. Таблица 2.1
2.2 Определяем передаточное число редуктора для четырёх вариантов двигателей. u = nном / nm , (2.3) гдеnном–частотавращенияприноминальномрежиме, об/мин; nт–частотавращения тихоходного вала, об/мин; и1 =2840/300 =9,46 и2 =1435/300 =4,78 и3 =955/300 =3,18 и4 =700/300 =2,3 Таблица 2.2
При выборе типа двигателя учитываем, что двигатель с большей частотой вращения (синхронной 3000 об/мин) имеют низкий рабочий ресурс, а двигатели с низкими частотами (синхронными 750 об/мин) весьма металлоёмки. Выбираем двигатель 4АМ112MA6У3 (Рном=3 кВт, nном=955 об/мин, передаточное число редуктора u=3,18 , что находится в диапазоне рекомендуемых значений u = 2,0…6,3. Силовые (мощность и вращающий момент) и кинематические (частота вращения и угловая скорость) параметры привода рассчитываем на валах, исходя из требуемой (расчётной) мощности двигателя Рдв и его номинальной частоты вращения nном. 2.3 Силовые и кинематические параметры привода Определяем частоту вращения, угловую скорость, мощность и вращающий момент на каждом валу. Вал 1 (быстроходный): 2.3.1 Определяем частоту вращения быстроходного вала, об/мин n1 =nдв =955 (2.4) 2.3.2 Определяем угловую скорость быстроходного вала, рад/с 𝜔1 =(𝜋∙n1)/30 , (2.5) где n1– частота вращения быстроходного вала, об/мин;  2.3.3 Определяем вращающий момент на быстроходном валу, Нм  (2.6) (2.6)где Р1 - требуемую мощность двигателя, кВт; Р1 =Рдв =3  Вал II (тихоходный): 2.3.4 Определяем частоту вращения тихоходного вала, об/мин  (2.7) (2.7)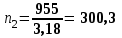 где u- передаточное число редуктора; 2.3.5 Определяем угловую скорость тихоходного вала, рад/с  (2.8) (2.8)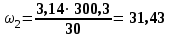 2.3.6 Определяем мощность тихоходного вала, кВт; 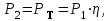 (2.9) (2.9)Р2 =РТ = 3 ·0,92 = 2,76 где η– общий КПД привода; 2.3.7 Определяем вращающий момент на тихоходномвалу, Нм; 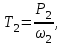 (2.10) (2.10) Угловая скорость от ведущего к ведомому валу уменьшается с 𝜔1 = 99,95 рад/с до 𝜔2 = 31,43 рад/с. За счет этого вращающий момент растёт от Т1 = 30 Нм до Т2 =87,8 Нм. 3Выбор материала зубчатых передач. Определение допускаемых напряжений Исходные данные: 𝜔1 = 99,95 рад/с 𝜔2 = 31,43 рад/с Lh= 12500ч 3.1 Выбор твердости, термообработки и материала зубчатых колес Выбираем материал зубчатых колёс: для шестерни принимаем Сталь 40ХН, для колеса Сталь 45, термообработка – улучшение. По таблице 3.2 [1 ] принимаем: для шестерни твёрдость 269…302 НВ, (285 НВ1ср), наибольший диаметр заготовки Dпред ≤ 200мм. для колеса твёрдость 235…262 НВ,(249 НВ2ср), наибольшая толщина сечения заготовки Sпред ≤80мм. При этом НВ1ср-НВ2ср=285-249=36 - обеспечивается прирабатываемость зубьев. 3.2 Определение допускаемых контактных напряжений для зубьев шестерни [σ]H1 и колеса [σ]H2 Определяем допускаемы контактные напряжения при расчетах на прочность отдельно на зубьев шестерни [σ]H1 и колеса [σ]H2 в следующем порядке: 3.2.1 Рассчитываем коэффициент долговечности KHL. Наработка за весь срок службы: для шестерни: N1 = 573·𝜔1 ·Lh(3.1) N1 = 573 ·99,95 ·12500 = 0,715 · 109 циклов для колеса: N2 = 573·𝜔2 ·Lh(3.2) N2 = 573 ·31,4 ·12500 = 0,22 · 109циклов Число циклов перемены напряжений NHO, соответствующий пределу выносливости находим по таблице 3.4 методом интерполирования: NHО1 = 22,45 · 106циклов; NHО2 = 16,37 · 106циклов; Так как N1 =715·106 > NHО1 = 22,45 · 106 и N2 = 220·106 > NHО2 = 16,37 · 106,, то коэффициенты долговечности KHL1 = 1 и KHL2 = 1. 3.2.2 По таблице 3.1 определяем допускаемы контактные напряжения [σ]НО, соответствующее число циклов перемены напряженийNHO: для шестерни [σ]НО1 = 1,8·НВ1ср + 67= 1,8·285 + 67= 580 Н/мм2 для колеса [σ]НО2 = 1,8·НВ2ср + 67=1,8·249 + 67= 515 Н/мм2 3.2.3 Определяем допускаемые контактные напряжения для шестерни и колеса [σ]Н,, Н/мм2 [σ]Н =К НL·[σ]НО , (3.3) где КНL - коэффициент долговечности, для прирабатывающихся колес К НL =1,0; [s]H1 = 1·580= 580 Н/мм2. [s]H2 = 1·515 = 515 Н/мм2. Расчет зубьев на контактную прочность ведем по меньшему значению []н =515Н/мм2 т. е. по менее прочным зубьям колеса. 3.3 Определяем допускаемые напряжения изгиба для зубьевшестерни [σ]F1 и колеса [σ]F2. 3.3.1 По таблице 3.1 определяем предел выносливости на изгиб NF0 , Н/мм2 [σ]F0 = 1,03·НВср , (3.4) для шестерни [σ]F01 = 1,03·НВ1ср = 1,03·285 = 294 Н/мм2; для колеса [σ]F02 = 1,03·НВ2ср = 1,03·249 = 256 Н/мм2; 3.3.2 Определяем допускаемые напряжения изгиба для шестерни и колеса, [σ]F , Н/мм2 [σ]F=КFL·[σ]FО ,(3.5) где KFL- коэффициент долговечности, для прирабатывающихся колес KFL= 1,0; [σ]F1 = 1,0·294= 294 Н/мм2; [σ]F2 = 1,0·256 = 256 Н/мм2; Расчёт модуля зацепления для цилиндрической зубчатой передачи выполняем по меньшему значению [σ]F, т.е. по менее прочным зубьям колеса [σ]F2 = 256 Н/мм2 3.4 Составляем табличный ответ к задаче
Таблица 3.1 - Механические характеристики материалов зубчатых колёс 4 Расчет зубчатой передачи редуктора 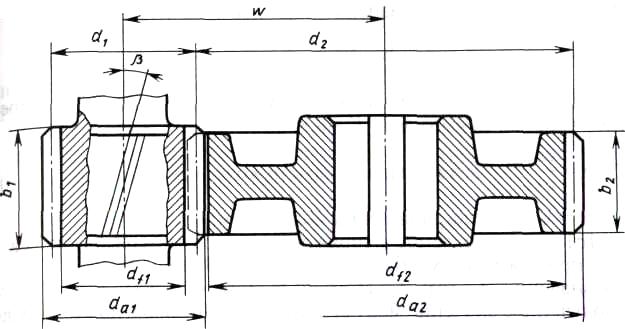 Рисунок 2 Геометрические параметры цилиндрической зубчатой передачи Определение геометрических параметров Проектный расчет 4.1 Определяем межосевое расстояние aw , мм  (4.1) (4.1)где Ка–вспомогательный коэффициент; для косозубых передач Ка = 43; ψва–коэффициент ширины венца колеса, равный 0,28...0,36 для шестерни, расположенной симметрично относительно опор; Кнβ– коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьевКнβ=1; Т2 – вращающий момент на тихоходном валу, Нм; Т2=87,8; [σ]H– допускаемое контактное напряжение колеса с менее прочным зубом, [σ]H= 515 Н/мм2 u = 3,18 – передаточное число редуктора. 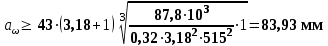 Принимаем стандартное значение aw= 85 4.2 Определяем модуль зацепления т, мм 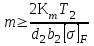 , (4.2) , (4.2)где Кmвспомогательный коэффициент; для косозубых передач Кm= 5,8; d2 делительный диаметр колеса, мм   b2 ширина венца колеса, мм b2 = ψваaw, b2 = 0,32·85 = 27,2 Принимаем b2 = 28 мм []F= []F2 –допускаемое напряжение изгиба материала колеса с менее прочным зубом, Н/мм2;  Полученное значение модуля mокругляем в большую сторону до стандартного значения. Принимаем m =1,25 4.3 Определяем суммарное число зубьев шестерни и колеса ZΣ= (2aw·cosβmin , /m), (4.3) где, угол наклона зубьев βmin= arcsin (3,5m/ b2) βmin= arcsin (3,5 ·1,25/28) = 8,98929 0 ZΣ= (2 ·85 ·соs8,98929/1,25) = 134,23 В косозубых передачах угол наклона зубьев принимают β = 8…15о, но из-за роста осевых сил Fa в зацеплении желательно получить его меньшее значение, варьируя величиной модуля т и шириной колеса b2 Полученное значение ZΣ округляем в меньшую сторону до целого числа. Принимаем ZΣ=134 4.4 Уточняем действительную величину угла наклона зубьев:  (4.4) (4.4)β = arcosβ 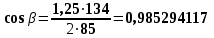 β = arcos0,985294117= 9,83822 о 4.5 Определяем число зубьев шестерни: Z1 = ZΣ/ (1+u), (4.5) Z1 = 134/ (3,18+1) = 32,05 Значение Z1 округляем до ближайшего целого числа. Принимаем Z1 = 32 Из условий уменьшения шума и отсутствия подрезания зубьев рекомендуется Z1 >18, данное условие выполняется. 4.6 Определяем число зубьев колеса: Z2 =ZΣZ1 , (4.6) Z2=134-32=102 4.7 Определяем фактическое передаточное число иф и проверяем его отклонение Δ u отзаданногозначения uф =Z2 /Z1 ,(4.7) uф= 102/32 = 3,187 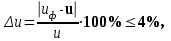 (4.8) (4.8)  Условия нормы отклонения передаточного числа выполняется 4.8 Определяем фактическое межосевое расстояние, мм aw=(m·ZΣ) /2 · cosβ, (4.9) aw=(134 ∙ 1,24)/2 · cos 9,83822 = 85,025мм 4.9 Определяем основные геометрические размеры колес:
Проверочный расчет 4.10 Проверяем межосевое расстояние aw= (d1 + d2)/2, (4.10) aw= (40,6+129,44)/2 = 85мм 4.11 Проверяем пригодность заготовок шестерни и колеса: колес Условия пригодности заготовок колес 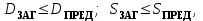 где Dпред и Sпред предельные размеры заготовок; Dзаг и Sзагразмеры заготовок колес; Для цилиндрической шестерни диаметр заготовки Dзаг = da1 + 6мм, Здесь 6мм припуск на механическую обработку. Dзаг =43,1+6= 49,1<200 Для колеса без выемок толщина сечения заготовки Sзаг= b2 + 4мм, Sзаг=27,2+4=31,2 < 125 Условия пригодности заготовок колес выполняются. 4.12 Проверяем контактные напряжения н , Н/мм2  , (4.11) , (4.11)где К вспомогательный коэффициент; для косозубых передач К = 376;  окружная сила в зацеплении (Н), окружная сила в зацеплении (Н),  Здесь Т2 –Нм, d2 – м 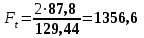 КНкоэффициент, учитывающий распределение нагрузки между зубьями. Для косозубых колес КНопределяется по графику на рисунке 4.2 [1] в зависимости от окружной скорости колес υ, м/систепениточностипередачи; Определяем окружную скорость  Здесь d2 - м, ω2 - рад/с.  Принимаем 8 степень точности передачи. КН= 1,07 КН коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи (таблица 4.2 ); КН= 1,02 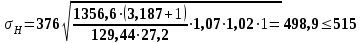 Условие прочности выполняется 4.13 Проверяем напряжения изгиба зубьев шестерни F1 и колеса F2 , Н/мм2  (4.12) (4.12)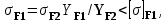 (4.13) (4.13)где KFaкоэффициент, учитывающий распределение нагрузки между зубьями, зависит от степени точности передачи. Для косозубых колес KFa=0,91; KFβ коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев колес KFβ=1; KF коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи (таблица 4.2 [1])KF=1,06 ; YF1 и YF2 коэффициенты формы зуба шестерни и колеса, определяются по таблице 4.3 интерполированием в зависимости от эквивалентного числа зубьев шестерни и колеса: Zv 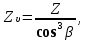   По таблице 4.3 коэффициенты формы зуба: шестерни YF1 = 3,75; колеса YF2 = 3,62. Yβ= 1-β0/ 140 0-коэффициент, учитывающий наклон зуба Yβ= 1-(10,830 0/ 140 0)= 0,9286 Расчетные напряжения изгиба в основании зубьев: колеса, , Н/мм2; 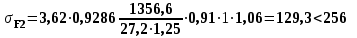 шестерни  Прочность зубьев на изгиб обеспечивается. 4.14 Составляем табличный ответ к задаче:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||