|
Задачи для ГТ, ГТБ. 1 семестр. 1. кинематика поступательного движения радиусвектор точки
c.
7.3. В лабораторной системе отсчета одна из двух одинаковых частиц с массой m0 покоится, другая движется со скоростью v=0,8с по направлению к покоящейся частице. Определите релятивистскую массу движущейся частицы в лабораторной системе отсчета и ее кинетическую энергию. Ответ: m=1,67 m0; Е=0,67 m0с2.
7.4. Электрон движется со скоростью v=0,6с. Определите его релятивистский импульс и кинетическую энергию Е. Ответ: р=2,05·10-22кг·м/с; Е=0,128 МэВ.
7.5. Импульс р релятивистской частицы равен m0c (m0-масса покоя). Определите скорость частицы v в долях скорости света и отношение массы движущейся частицы к ее массе покоя m/m0. Ответ: v=0,71с; m/m0=1,41.
7.6. Полная энергия α-частицы возросла в процессе ускоренного движения на  Е=56,4МэВ. На сколько при этом изменится масса частицы? С какой скоростью движется частица? Массой покоя α-частицы m0=4 а.е.м. Ответ: Е=56,4МэВ. На сколько при этом изменится масса частицы? С какой скоростью движется частица? Массой покоя α-частицы m0=4 а.е.м. Ответ:  m=1,5m0; v=0,917с. m=1,5m0; v=0,917с.
7.7. Предположим, что мы можем измерить длину стержня с точностью Δl = 0,1 мкм. При какой относительной скорости u двух инерциальных систем отсчета можно было бы обнаружить релятивистское сокращение длины стержня, собственная длина которого l0=1 м? Во сколько раз изменится масса стержня, при движении его с рассчитанной скоростью u относительно неподвижной системы отсчета? Ответ: u=134 км/с; m/m0 = 1,114.
7.8. Собственное время жизни некоторой нестабильной частицы τ0= 10 нс. Найти скорость частицы и путь, который пролетит эта частица до распада, в лабораторной системе отсчета, где время её жизни  = 20нс. Ответ: v = 0,87c; S = 5,2 м. = 20нс. Ответ: v = 0,87c; S = 5,2 м.
7.9. μ- мезон, рождённый в верхних слоях земной атмосферы, движется со скоростью V = 0,99с относительно земли и пролетает от места своего рождения до точки распада расстояние l = 3 км. Определить собственное время жизни этого мезона и расстояние, которое он пролетит в этой системе отчёта «с его точки зрения». Ответ: τ0=1,4 мкс; l0=420 м.
7.10. Два стержня одинаковой собственной длины l0 движутся в продольном направлении навстречу друг другу параллельно общей оси с одной и той же скоростью v=0,8с относительно лабораторной системы отсчёта. Во сколько раз длина каждого стержня l в системе отсчёта, связанной с другим стержнем, отличается от собственной длины? Ответ: l0/l=4,6.
7.11. На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными. Скорость спутника v=7,9км/с. На сколько отстанут часы на спутнике по измерениям земного наблюдателя за промежуток времени 0,5 года? Как отличаются значения кинетической энергии спутника, если расчет провести по классической и релятивистской формулам? Масса покоя спутника составляет 10 тонн. Ответ: Δτ=5,4·10-3 с; не отличаются.
7.12. Какая относительная погрешность будет допущена, если расчёт импульса частицы, движущейся со скоростью: 1) 10 км/с, 2) 103км/с, 3) 105 км/с, 4) 0,9с. Произвести в рамках классической механики? Ответ: 1) ррел/ркласс =1; 2) ррел/ркласс= 1; 3) ррел/ркласс = 1,06; 4) ррел/ркласс = 2,3.
7.13. Какую работу необходимо совершить, чтобы скорость частиц, с массой покоя m0, изменилась от 0,6с до 0,8с? Сравнить полученный результат со значением работы, вычисленным по классической формуле. Ответ: Арел=0,417m0c2; A класс =0,14 m0c2.
7.14. Фотонная ракета движется относительно земли с такой скоростью, что по часам наблюдателя на Земле, ход времени в ней замедляется в 1,25 раз. Какую часть от скорости света составляет скорость движения ракеты? На сколько изменятся ее линейные размеры в направлении движения, если первоначально длина ракеты составляла 35м? Ответ: v=0,6c; Δl=7 м.
7.15. Частица с массой покоя m0 в момент времени t = 0 начинает двигаться под действием постоянной силы F. Найти зависимость скорости V частицы от времени t. Построить качественно график V(t). Ответ: 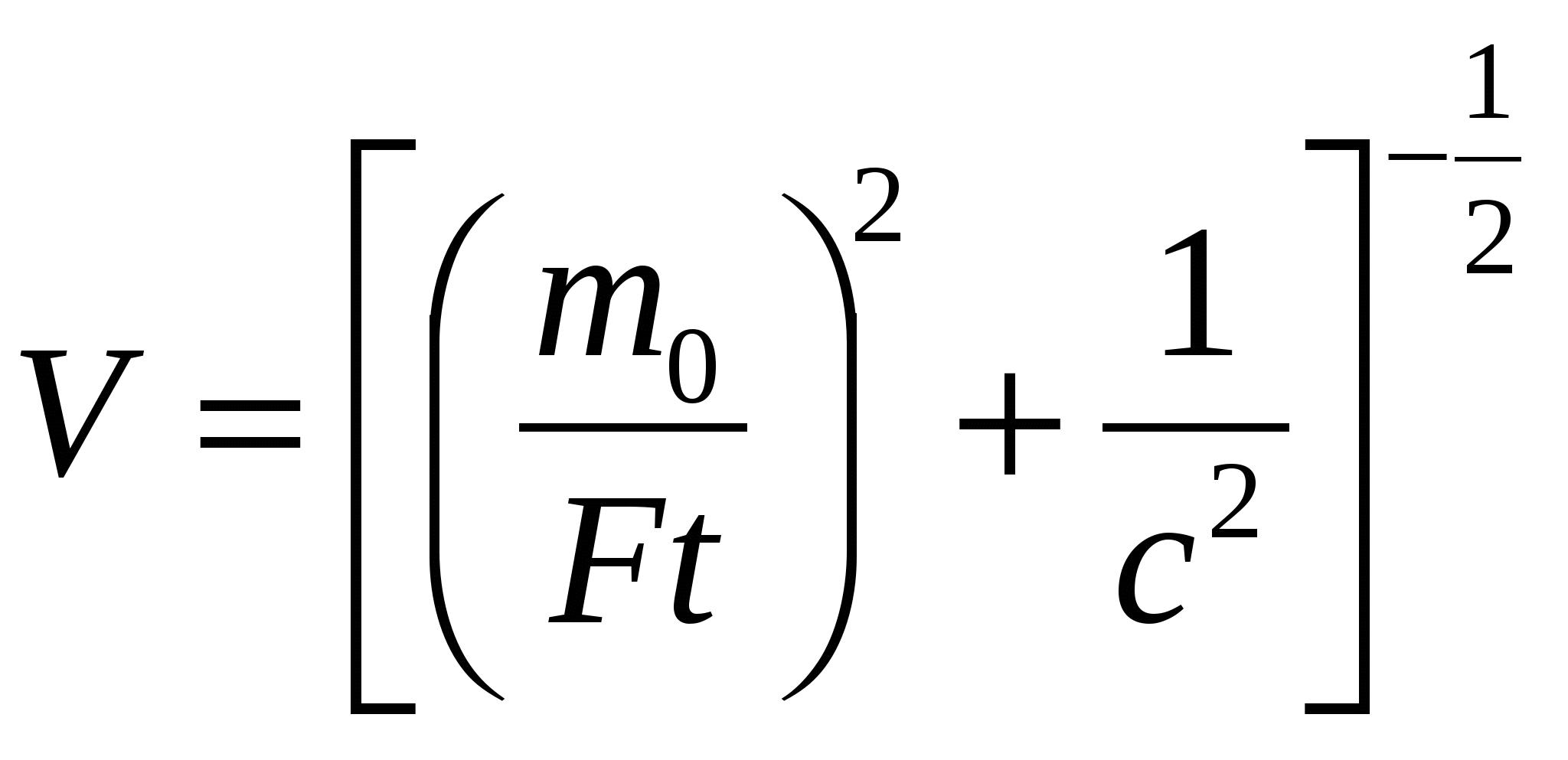 . .
7.16. Импульс релятивистского электрона равен 3·10-22 кг·м/с. Найти кинетическую энергию этого электрона. Ответ: E=0,25 МэВ.
7.17. Собственное время жизни μ - мезона равно τ0 = 2 мкс. От точки рождения до точки распада мезон пролетает относительно земли расстояние 6 км. С какой скоростью двигался мезон? Ответ: v=0,995c.
7.18. Кинетическая энергия ускоряемого протона возросла до 3·10-10 Дж. Во сколько раз изменилась при этом масса протона? Какова скорость протона? Ответ: m/m0=3; v=2,8∙108 м/с.
7.19. Две релятивистские частицы движутся в лабораторной системе отсчета со скоростями v1=0,6с и v2=0,9с вдоль одной прямой. Определите их относительную скорость в двух случаях: 1)частицы движутся в противоположных направлениях, 2)частицы движутся в одном направлении. Чему равна кинетическая энергия первой частицы в системе отсчета связанной со второй, если первая частица - протон? Ответ: 1) v=0,974с, Е1,2=510 пДж; 2) v=0,195с, Е1,2=300 пДж.
7.20. С какой скоростью (в долях от скорости света) должен двигаться электрон, чтобы его масса возросла на 6·10-31 кг. Какую кинетическую энергию имеет электрон при такой скорости? Ответ: v=0,8c; E = 0,34 Мэв.
7.21. Кинетическая энергия движущегося тела в 2 раза превышает энергию покоя. Во сколько раз уменьшается при этом видимый размер тела в направлении движения? Какова скорость тела? Ответ: l0/l=3; v=0,94c.
7.22. Масса движущейся частицы увеличилась в 1,5 раза. Какую скорость имеет частица? Какая относительная ошибка будет допущена, если кинетическую энергию частицы в этих условиях рассчитывать классическим образом? Ответ: v=0,75c; ΔE/Eрел=0,44.
7.23. Электрон ускорен в электрическом поле с разностью потенциалов U=106 В. Вычислить скорость электрона и его кинетическую энергию методами: 1) классической механики, 2) релятивистской механики. Оценить полученные данные. Ответ: 1) v=6·108м/с; Е=106 эВ. 2) v=0,94c; E=10 6 эВ.
7.24. Электрон в ускорителе прошёл ускоряющую разность потенциалов U=102 кВ. Во сколько раз увеличилась масса частицы? Вычислите его кинетическую энергию. Ответ: m/m0=1,2; 1,6∙10-14Дж.
7.25. Первоначально кинетическая энергия релятивистской частицы была равна ее энергии покоя, а затем при ускоренном движении возросла в 4 раза. Во сколько возрастет при этом импульс частицы? С какой скоростью (в долях скорости света) двигалась частица первоначально? Ответ: р2/р1=2,84; v=0,87c.
29. ВОЛНЫ де БРОЙЛЯ
Дебройлевская длина волны движущейся частицы:
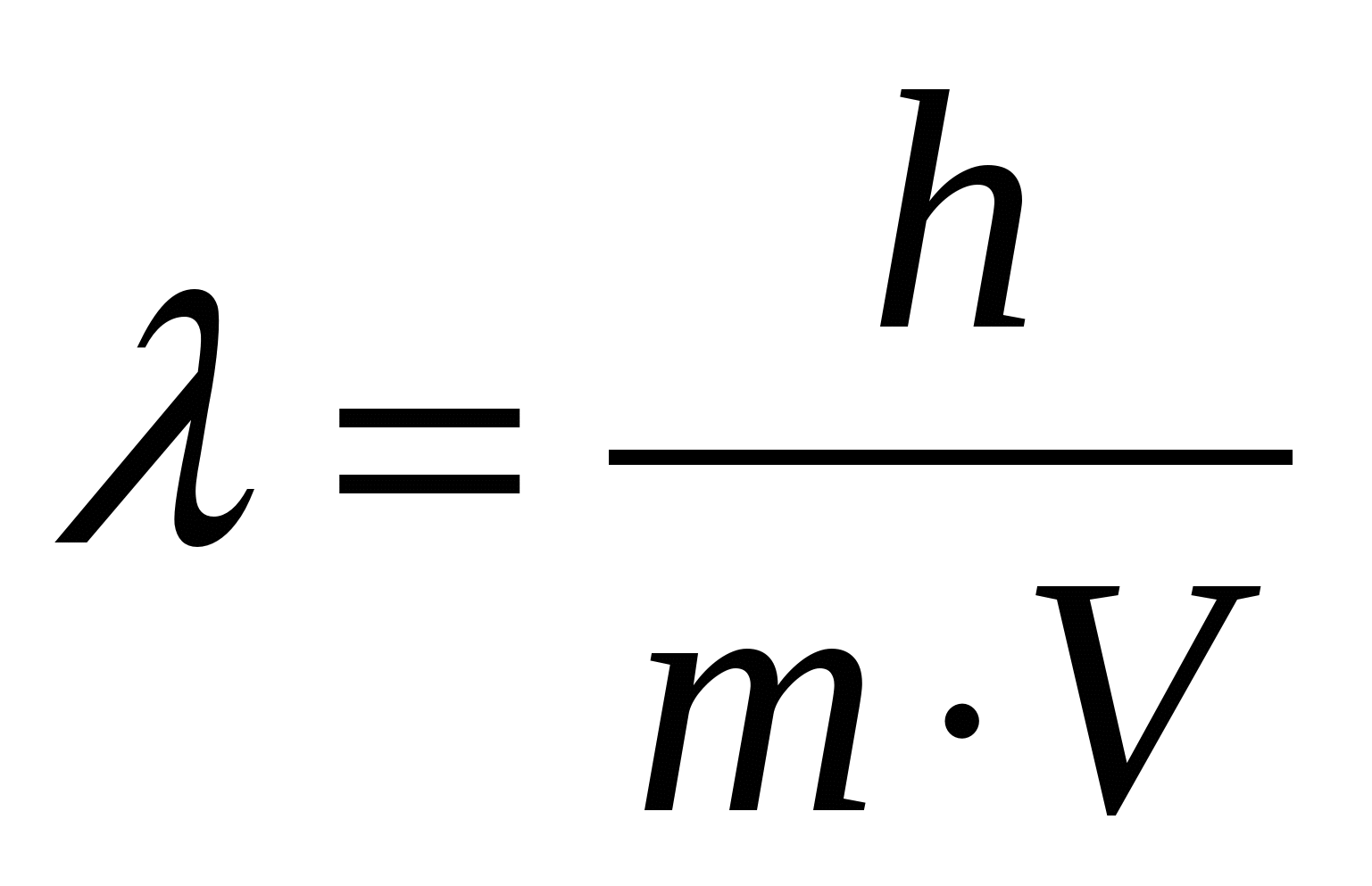 , ,
где h-постоянная Планка, m-масса частицы, V-ее скорость.
29.1. Какую энергию нужно дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 200 пм до 150 пм? Ответ: 28,9 эВ.
29.2. Электрон обладает кинетической энергией 30 эВ. Определить дебройлевскую длину волны электрона. Во сколько раз изменится эта длина волны, если кинетическая энергия уменьшится на 20%? Ответ: 2,2∙10-10 м; 1,12.
29.3. Вычислить дебройлевские длины волн электрона, протона и атома урана, имеющих одинаковые кинетические энергии 200эВ. Ответ: 87 пм; 2 пм; 0,13 пм.
29.4. Найти дебройлевские длины волн для молекул азота и водорода, имеющих наиболее вероятные скорости при нормальных условиях. Ответ: 3,5∙10-11 м; 13,2∙10-11 м.
29.5. Дебройлевская длина волны протона при его ускорении в электрическом поле уменьшилась от 10-10 м до 3∙10-11 м. На сколько увеличилась энергия протона? Ответ: 0,83 эВ.
29.6. Какова дебройлевская длина волны электрона, имеющего кинетическую энергию 1 МэВ? Ответ: 0,12 пм.
29.7. Вычислить дебройлевские длины волн для электрона и протона, прошедших одинаковую ускоряющую разность потенциалов 10 В. Ответ: 390 пм; 9,1пм
29.8. На какую величину и на сколько процентов по отношению к нормальным условиям должна измениться температура идеального газа, чтобы дебройлевская длина волны его молекул уменьшилась на 10%? Ответ: 64 К; 23%.
29.9. Какую укоряющую разность потенциалов в электрическом поле должна пройти α-частица, чтобы ее дебройлевская длина волны уменьшилась от 180 пм до 50 пм? Ответ: 0,04 В.
29.10. α-частица была ускорена в электрическом поле с разностью потенциалов Δφ. При этом на выходе из поля ее дебройлевская длина волны оказалась равной 2,62 пм. Какую дебройлевскую длину волны будет иметь позитрон, если его ускорить в этом же электрическом поле? Ответ: 31,6 пм.
29.11. Какую ускоряющую разность потенциалов должен пройти релятивистский электрон, чтобы его дебройлевская длина волны оказалась равной 1,8 пм? Ответ: 350 кВ.
29.12. Найти дебройлевскую длину волны протонов, движущихся со скоростью 0,9с (где с – скорость света). Во сколько раз изменится эта длина волны, если кинетическая энергия протона уменьшится в 1000 раз? Ответ: 6,3∙10-16 м; 41.
29.13. Атом водорода, находящийся первоначально в основном состоянии, поглотил фотон с энергией 17 эВ. Какую дебройлевскую длину волны будет иметь выбитый электрон вдали от атома? Ответ: 0,667 нм.
29.14. Фотон с длиной волны 82 нм ионизирует атом водорода, который находился в невозбужденном состоянии. Какую дебройлевскую длину волны будет иметь образовавшийся свободный электрон? Ответ: 1нм.
29.15. Электрон обладает кинетической энергией 1,02 МэВ. Во сколько раз изменится его дебройлевская длина волны, если кинетическая энергия уменьшится вдвое? Ответ: 1,6 раза.
29.16. Электрон движется по окружности радиусом 1 см в однородном магнитном поле с индукцией 0,05 Тл. Какова дебройлевская длина волны этого электрона? Ответ: 8,3 пм.
29.17. Пучок параллельно движущихся электронов, имеющих скорости 106 м/с, падает нормально на диафрагму с длинной щелью шириной 1 мкм. На экране за щелью на расстоянии 0,5м образуется дифракционная картина. Определить линейное расстояние между дифракционными минимумами первого порядка. Ответ: 0,36 мм.
29.18. α-частица, движущаяся по окружности радиусом 10 см в однородном магнитном поле, длину волны, равную 10 пм. Найти индукцию магнитного поля, в котором движется частица. Ответ: 2 мТл.
29.19. Найти дебройлевскую длину волны электрона, движущегося по круговой орбите в атоме водорода, находящегося в основном состоянии. Сравнить ее с длиной орбиты. Ответ: 3,3∙10-10 м.
29.20. Во сколько раз изменяется дебройлевская длина волны электрона при переходе его в атоме водорода из основного энергетического состояния в первое возбужденное? Ответ: 2.
29.21. Сколько дебройлевских длин волн укладывается на длине орбиты электрона в атоме водорода: 1) в невозбужденном состоянии? 2) в первом возбужденном состоянии? 3) на пятой орбите? Ответ:1, 2, 5.
29.22. Из теории Бора для атома водорода следует, что стационарными для электронов атома являются такие орбиты, на длине которых укладывается целое число длин дебройлевских волн. Исходя из этого, найдите числовые значения момента импульса электрона в атоме водорода на первых трех боровских орбитах. Ответ:1,05∙10-34 Дж∙с; 2,1∙10-34 Дж∙с; 3,16∙10-34 Дж∙с.
29.23. Поток одинаково ускоренных электронов падает нормально на щель шириной 0,2 мкм. В дифракционной картине за щелью минимум второго порядка наблюдается под углом 2,90. Найти по этим данным разность потенциалов ускоряющего электрического поля. Ответ: 0,06 В.
29.24. Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной шириной 1 мкм. Определить скорости этих электронов, если на экране, расположенном от щели на расстоянии 50 см, ширина центрального дифракционного максимума равна 0,36 мм. Ответ: 2∙106 м/с.
29.25. Известно, что движущиеся нерелятивистские протон и альфа-частица имеют одинаковые дебройлевские длины волн. Во сколько раз отличаются их кинетические энергии? Ответ: 4.
30. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ
Соотношение неопределенностей для координаты и импульса:
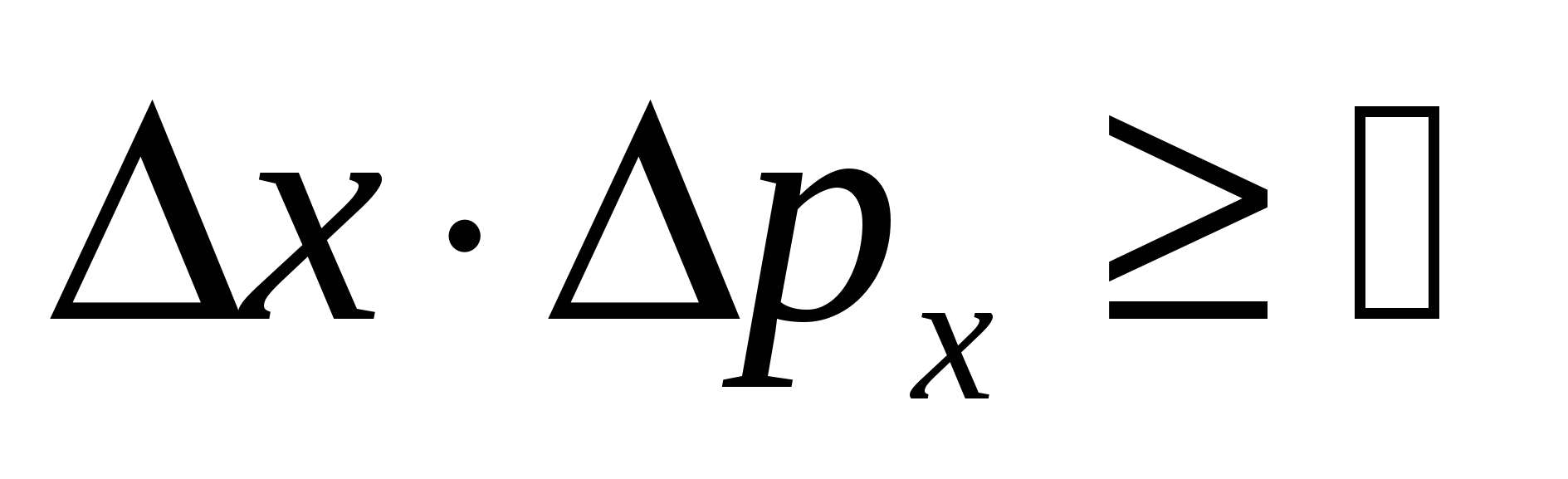 . .
Соотношение неопределенностей для энергии и времени:
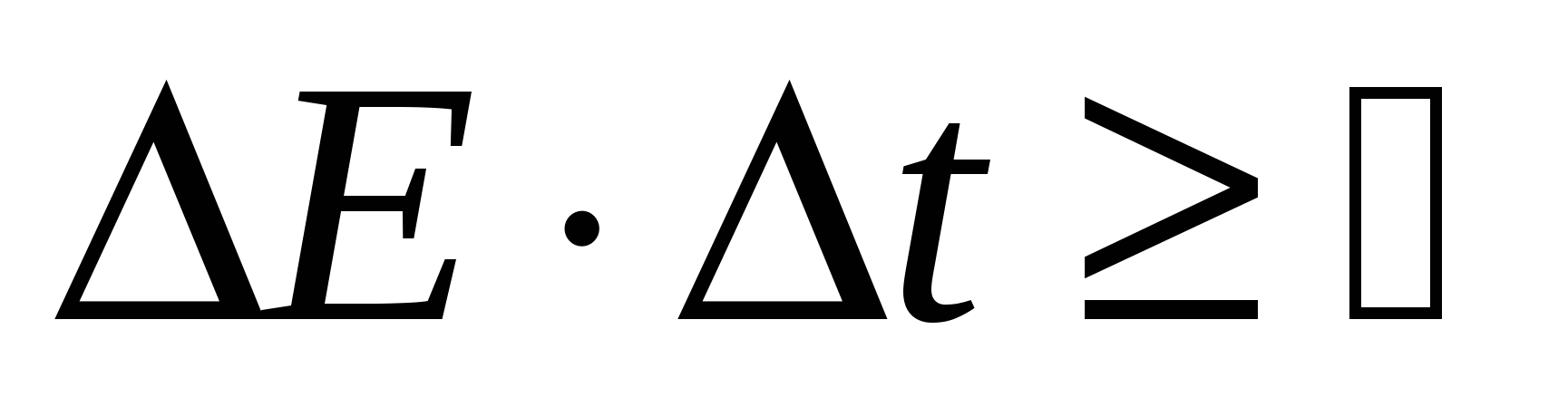 . .
30.1. Определить неточность в определении координаты электрона, движущегося в атоме водорода со скоростью 2,2 Мм/с, если допустить, что неточность в определении скорости составляет 10% от ее величины. Сравнить полученную неточность с размером атома и выяснить, применимо ли понятие «траектории» в данном случае. Ответ: 0,53 нм.
30.2. Оценить с помощью соотношения неопределенностей неопределенность скорости электрона в атоме водорода, полагая, что размер атома равен 0,2 нм. Сравнить полученное значение со скоростью электрона на первой боровской орбите данного атома. Можно ли применять классическую механику для описания поведения электрона в атоме водорода? Ответ: 0,6 Мм/с.
30.3. При движении частицы вдоль оси x скорость ее может быть определена с точностью (ошибкой) до 1 см/с. Найти неопределенность координаты, если частицей является: 1) электрон, 2) дробинка массой 0,1г. Ответ: 0,01м; 10-28м.
30.4. Сравнить неопределенность в определении скорости α-частицы (энергия 6Мэв), если ее координата установлена с точностью до 10-5 м, и шарика массой 10-4 кг, если координата его центра тяжести определена с такой же точностью. Какую механику (классическую или квантовую) необходимо использовать в данном случае для описания поведения этих частиц? Ответ: 1,6∙10-3м/с, 10-25м/с, классическая.
30.5. Электрон с кинетической энергией 15 эВ находится в металлической пылинке диаметром 1 мкм. Оценить относительную неточность, с которой может быть определена скорость электрона. Ответ: 5∙10-3 %.
30.6. Моноэнергетический поток электронов с энергией 10 эВ падает на щель шириной а. Можно считать, что когда электрон проходит через цель, его координата известна с неточностью Δx=а. Оценить получаемую при этом относительную неточность в определении импульса Δр/р электрона в двух случаях: 1) а =100нм, 2) а =0,1нм. В каком случае можно пользоваться классической механикой? Ответ: 6,2∙10-4; 0,62.
30.7. Пылинки массой по 10-12 г взвешены в воздухе и находятся в тепловом равновесии с ним. Можно ли установить, наблюдая за движением пылинок, отклонение от законов классической механики? Принять, что воздух находится при нормальных условиях, пылинки имеют сферическую форму, плотность вещества пылинок равна 2∙103 кг/м3. Ответ: нет.
30.8. Во сколько раз дебройлевская длина волны частицы меньше неопределенности Δx ее координаты, которая соответствует относительной неопределенности импульса в 1% ? Ответ:
16.
30.9. Предполагая, что неопределенность координаты движущейся частицы равна дебройлевской длине волны, определить относительную неточность в определении импульса этой частицы. Ответ: 0,16.
30.10. Используя соотношение неопределенностей для координаты и импульса найти выражение, позволяющее оценить минимальную кинетическую энергию электрона, находящегося в одномерной бесконечно глубокой потенциальной яме шириной ℓ. Ответ: ђ2/(2mℓ2).
30.11. Используя соотношение неопределенностей оценить минимальную кинетическую энергию электрона в атоме водорода. Принять, что линейный размер атома
0,1 нм. Ответ:
4 эВ.
30.12. Показать, используя соотношение неопределенностей, что в ядре не могут находится электроны. Линейные размеры ядра принять равными 5 фм.
30.13. Приняв, что минимальная энергия нуклона в ядре равна 10 МэВ, оценить, исходя из соотношения неопределенностей, линейные размеры ядра. Ответ: 1,4 фм.
30.14. Электронный пучок ускоряется в электронно-лучевой трубке напряжением 500 В. Принимая, что неопределенность импульса равна 0,1% импульса электрона, найти неопределенность его координаты. Ответ: 8,7∙10-9м.
30.15. Ширина следа электрона, обладающего энергией 1,5 кэВ, на фотопластинке, полученного с помощью камеры Вильсона, составляет Δx=1 мкм. Можно ли по этому следу обнаружить отклонение в движении электрона от законов классической механики? Ответ: Δр/р = 5∙10-6; нет.
30.16. Электронный пучок ускоряется напряжением 1 кВ. Известно, что неопределенность скорости электронов составляет 10-3 от ее числового значения. Найти неопределенность координаты электрона. Являются ли электроны в данных условиях классическими частицами? Ответ: 6,2∙10-9 м.
30.17. Определить отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10-5 м, и пылинки массой 10-12 кг, если ее координата установлена с той же точностью. Ответ:
1018 .
30.18. Электронный пучок выходит из электронной пушки, ускоренный разностью потенциалов 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 пм (порядка диаметра атома) и его скорость с точностью 10% . Ответ: нет.
30.19. Электрон находится в одномерной прямоугольной потенциальной яме с очень высокими стенками. Ширина ямы ℓ. Оценить с помощью соотношения неопределенностей силу давления электрона на стенки ямы при минимально возможной его энергии. Ответ: |
|
|
 Скачать 0.61 Mb.
Скачать 0.61 Mb.
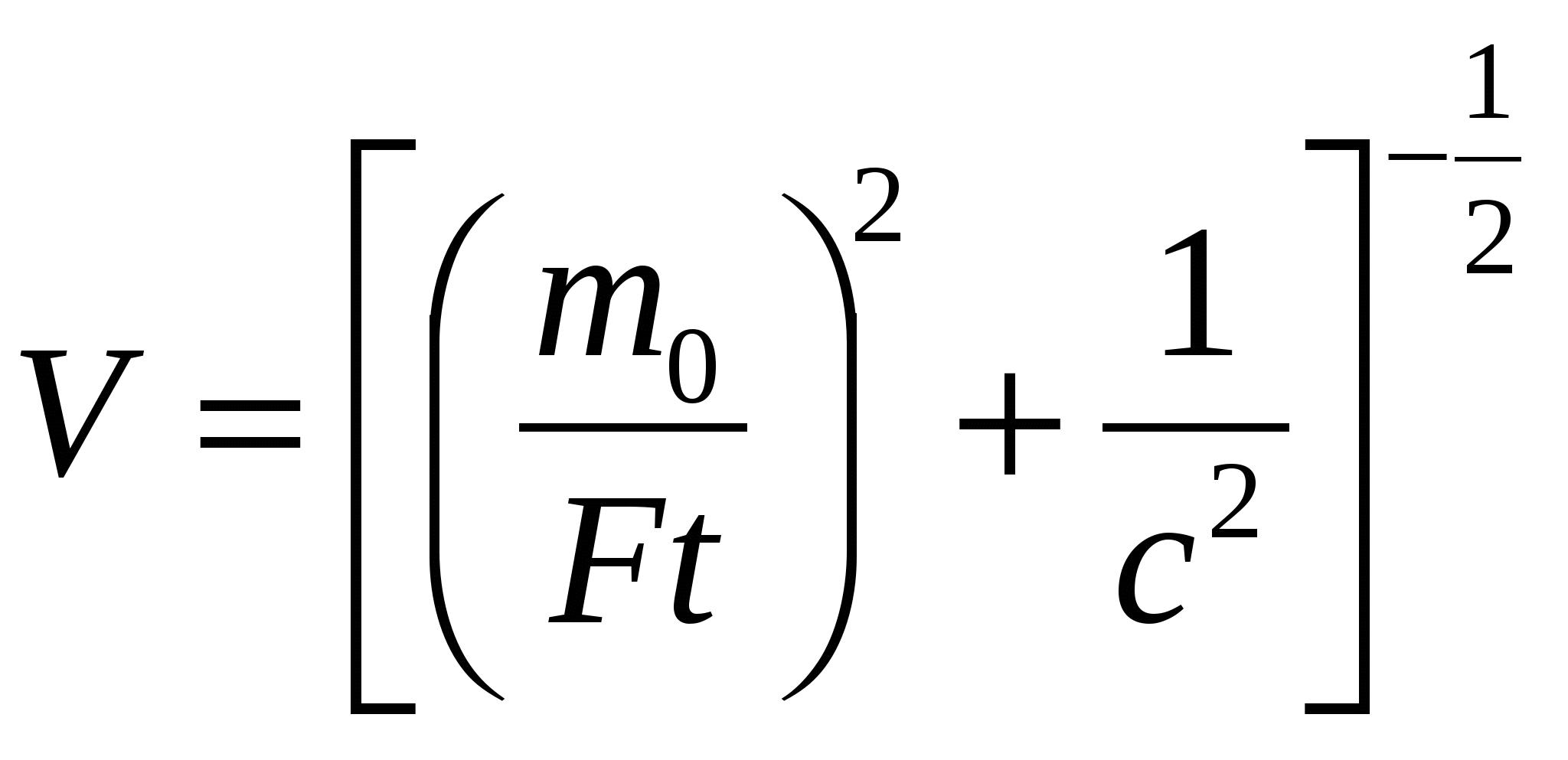 .
.