жбк. 1 компоновка и выбор типа балочной клетки

• Название: 1 компоновка и выбор типа балочной клетки
• Дата: 25.03.2023
• Размер: 1.91 Mb.
• Имя файла: Ð_Ñ_имеÑ_ Ñ_аÑ_Ñ_еÑ_а по Ð_Ð 1.docx
• Тип: Документы; #1014116
• страница: 3 из 3

Подбор сечения сплошной центрально-сжатой колонны
Геометрическая высота колонны
𝓁 = 6,5 -0,01 -0,27-1,1 +0,6 = 5,72 м
Расчётная продольная сила, действующая на колонну, равна сумме опорных реакций от двух главных балок опирающихся на неё
N = 2 · Q_max = 2· 694,8=1389,6 кН,
Материал колонны – сталь С245, расчётное сопротивление которой при t =1,5-20 мм R_у= 240 МПа = 24 кН/см². Коэффициент условий работы γ_с=1.

Принимаем сечение стержня колонны двутавровым, сваренным из трех листов.

Расчетная длина стержня колонны

𝓁_ef = 0,7𝓁= 0,7· 5,72 = 4,0 м.

Задаемся гибкостью λ=70 (для сплошных колонн при N =1500…2500 кН можно принять в пределах λ =100…70; при N = 2500…4000 кН - λ =70…50).
Условная гибкость колонны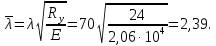
Из таблицы 4 определяем тип кривой устойчивости – тип «b».
Таблица 4.2 Значения коэффициентов α и β в зависимости от типа сечения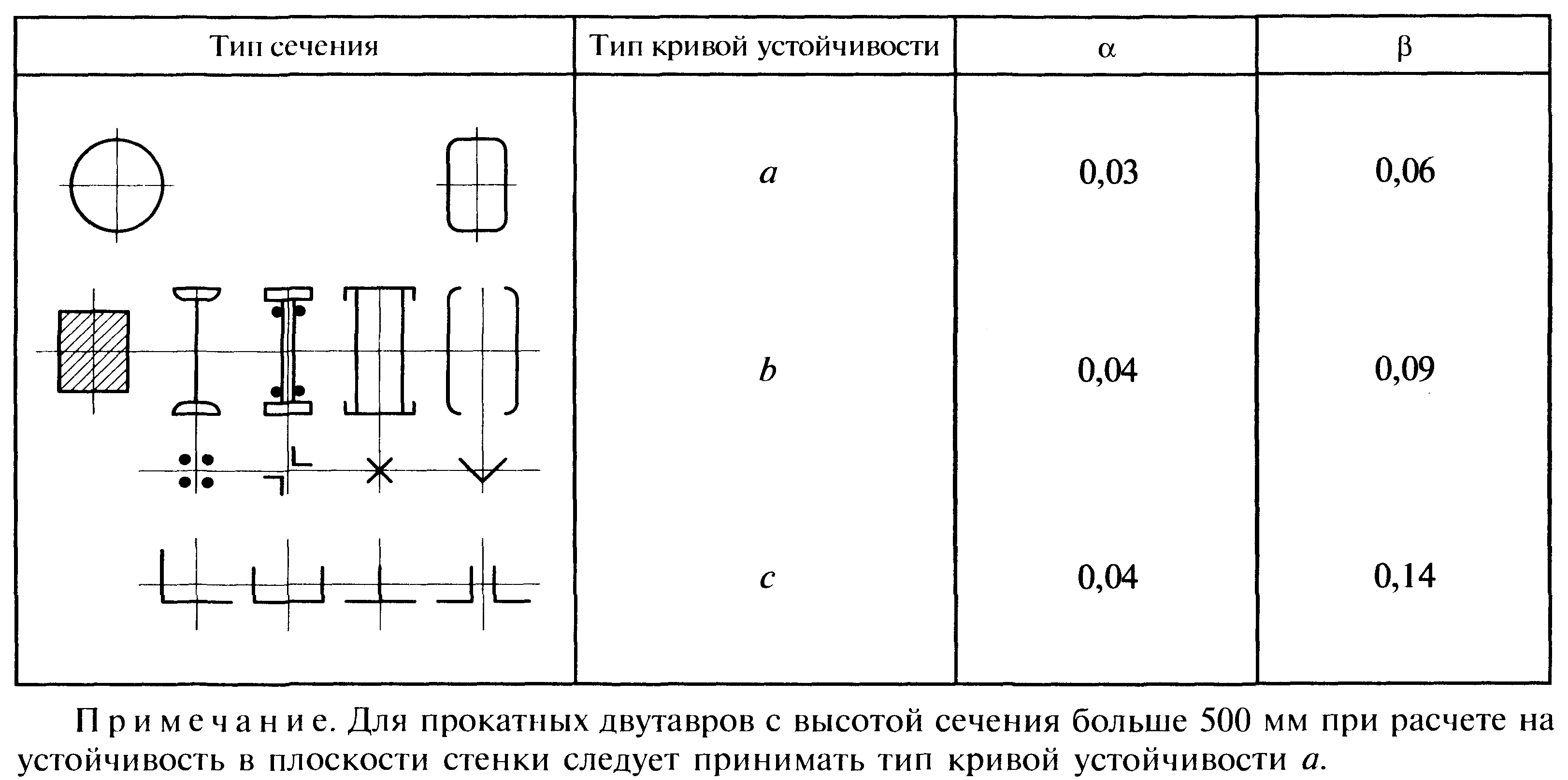



В соответствии с рекомендацией проекта новых норм, по таблице 4.3

находим соответствующее заданной условной гибкости значение коэффициента устойчивости φ при центральном сжатии. Для кривой типа b φ = 0,672.

Предварительно определяем требуемые:

площадь сечения колонны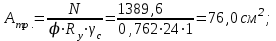
радиус инерции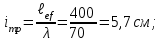
ширина сечения по табл. 3.1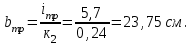

Принимаем bтр = bf = hw = 24 см.
Таблица 4.3 Коэффициент устойчивости при центральном сжатии φ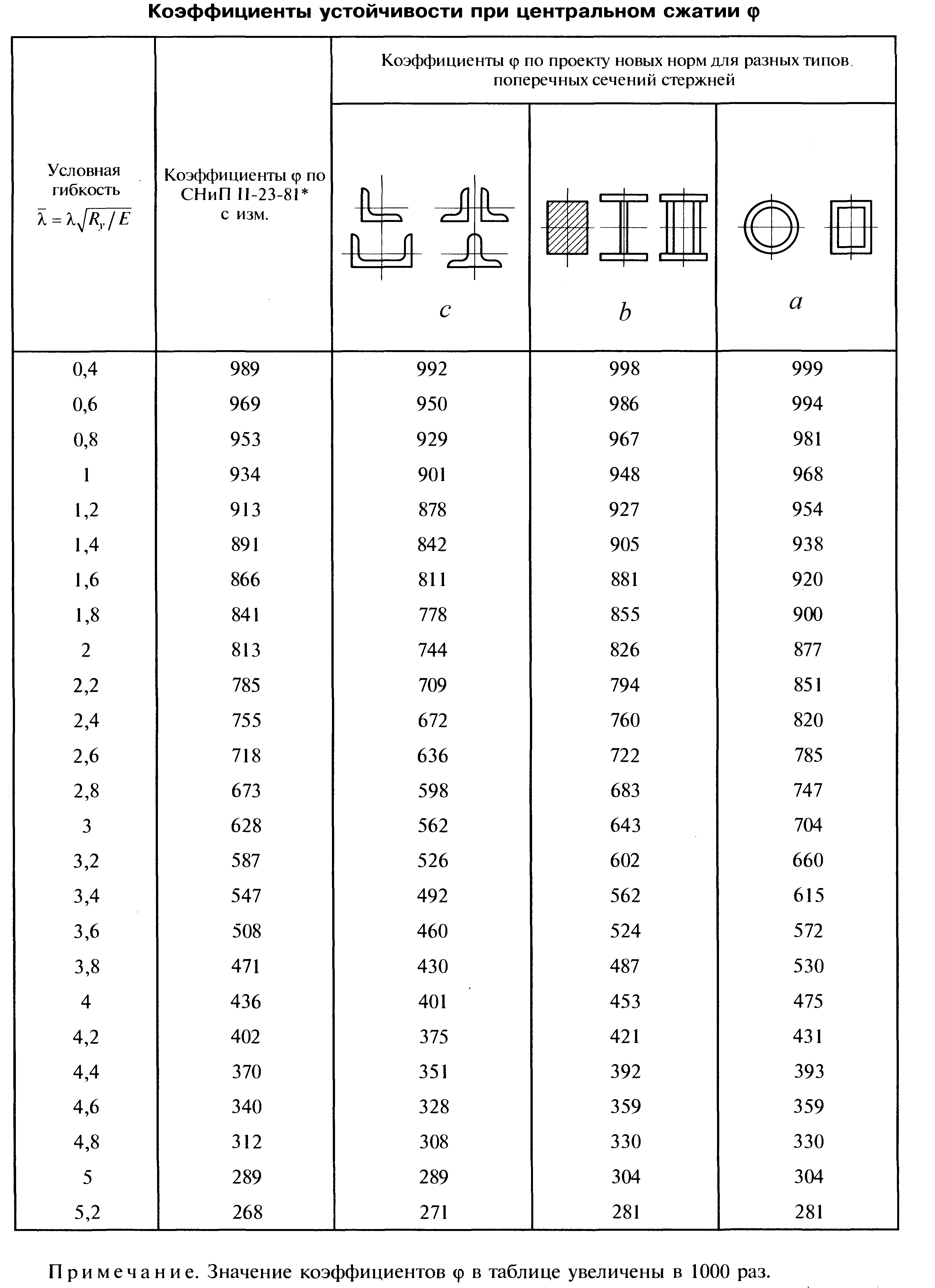



Для обеспечения равноустойчивости колонны в обеих плоскостях следует стремиться к такому распределению общей площади сечения, чтобы около (70 80) % ее приходилось на долю поясов. Тогда толщина пояса и стенки колонны будут равны соответственно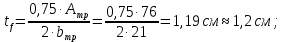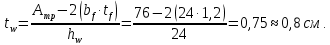


Полная площадь поперечного сечения колонны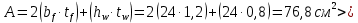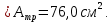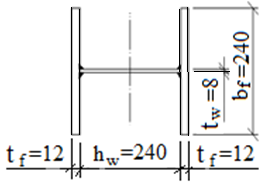





Рисунок 4.7. Сечение колонны со сплошной стенкой
Проверяем общую устойчивость колонны относительно оси «у»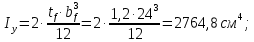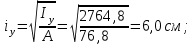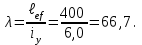


Условная гибкость колонны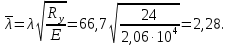
По проекту новых норм (таблица 4.3) для кривой типа «b» коэффициент устойчивости при центральном сжатии φ = 0,78.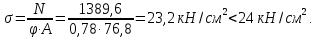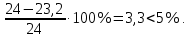


Запас прочности не превышает 5%, поэтому принимаем сечение без изменения.

Проверяем местную устойчивость стенки колонны.

Стенка колонны будет устойчивой, если условная гибкость стенки

не превысит предельную условную гибкость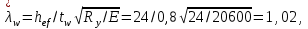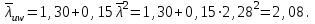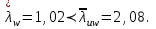



Условие выполняется, значит, стенка колонны устойчива.
Проверяем местную устойчивость поясных листов колонны.

Устойчивость поясных листов центрально-сжатых элементов считается обеспеченной, если условная гибкость свеса сжатого пояса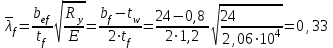


не превышает значений предельной условной гибкости пояса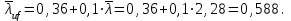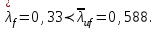



Условие выполняется, т.е. полка колонны устойчива.

Расчет базы сплошной колонны
Материал базы – сталь С245, расчетное сопротивление которой при толщине t_w = 1,5-20 мм по табл.51 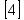R_y = 24 кН/см². Бетон фундамента В10 – расчётное сопротивление для первой группы предельных состояний по таблице 3.2 R_b = 6 МПа = 0,6 кН/см².

Расчётная сила давления на фундамент
N = F + G_кол. =1389,6 + 3,55 = 1393,15 кН.
Здесь G_кол = A · H · ρ_s· γ_f · g = 0,00768·5,72·7,85·1,05·9,81 = 3,55 кН – вес колонны;

А – площадь сечения колонны; Н - геометрическая высота колонны; ρ_s = 7,85 т/м³ – плотность стали; γ_f – коэффициент надёжности по нагрузке от веса колонны; g = 9,81 м/с² – ускорение свободного падения.

Требуемая площадь опорной плиты базы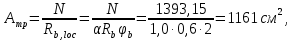


где 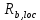– расчётное сопротивление бетона смятию; α = 1 для бетона класса ниже В25, для бетона классов В25 и выше 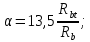φ_b принимают не более 2,5 для бетонов класса выше В7,5 и для бетонов класса В3,5; В5; В7,5 не более 1,5.

Считая в первом приближении плиту базы квадратной, будем иметь стороны плиты равными B = L = 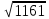= 34,1 см. Принимаем размер плиты B = L= 35 см. Уточняем площадь плиты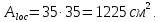
Напряжение под плитой .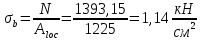
Конструируем базу колонны с траверсами, привариваем их к полкам колонны и к опорной плите угловыми швами. Вычисляем изгибающие моменты на разных участках для определения толщины плиты. В плите имеются три участка с различным количеством опертых кантов.

На участке 1 плита опёрта на четыре канта (рис.4.8). Соотношение сторон b/a = 24/11,6 = 2,07 ˃ 2. а = (а₁- t_w)/2 = (240-8)/2 = 116 мм, здесь t_w – толщина стенки стержня колонны.
Изгибающий момент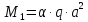

= 0,125 ·1,14 ·11,6² =19,2 кН·см,
где q – расчётное давление на 1 см² плиты, равное напряжению в фундаменте под плитой; α = 0,125 - коэффициент, зависящий от отношения более длинной стороны участка «b» к более короткой «a», принимаемый по таблице 3.3.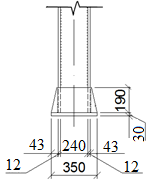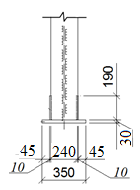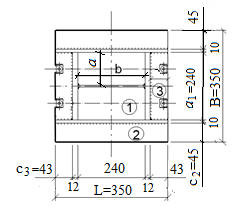



Рисунок 4.8. База центрально сжатой колонны
На участке 2 плита работает как консоль длиной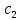
с₂ = (В – а₁ – 2t_tr)/2 = (350 – 240 – 2·10)/2 =45 мм, где t_tr – толщина траверсы.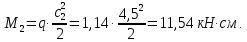



На участке 3 плита опёрта на три канта, где коэффициент α зависит от отношения закреплённой стороны к незакреплённой c₃/a₁= 4,3/24 = 0,179 ˂ 0,5. При таких соотношениях сторон участка плита работает тоже как консоль с длиной консоли c₃ = (L – b – 2·12)/2 = (350-240-2⋅12)/2 = 43 мм. Здесь 12 мм – толщина пояса колонны.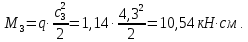

Определяем толщину опорной плиты по максимальному моменту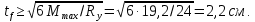

Принимаем плиту толщиной t_f = 30 мм.

Расчёт траверсы. Считаем в запас прочности, что усилие на плиту передаётся только через швы, прикрепляющие стержень колонны к траверсам.

Прикрепление траверсы к колонне выполняется полуавтоматической сваркой в углекислом газе сварочной проволокой Св08Г2С. Толщину траверс принимаем t_tr = 10 мм. По табл.56 расчётное сопротивление металла шва R_wf = 215 МПа = 21,5 кН/см². По табл. 3 расчётное сопротивление металла границы сплавления R_wz =0,45R_un и по табл. 51 для стали С245 R_un = =370 МПа = 37 кН/см².

Определяем расчётное сечение соединения. Задаёмся катетом шва (k_f ≤1,2t_min) k_f = 12 мм, тогда по табл. 35 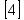β_f = 0,8; β_z = 1.

β_f · R_wf = 0,8·21,5 = 17,2 ˃ β_z · R_wz =1· 0,45·37 = 16,65 кН/см²,
таким образом, расчётным сечением является сечение по металлу границы сплавления_.

Расчётная длина шва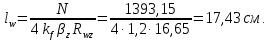

Высота траверсы
h_tr = ℓ_w + 1 = 17,43 + 1 = 18,43 см.
Принимаем h_tr = 19 см. Проверяем прочность траверсы как балки с двумя консолями. Изгибающий момент в середине пролёта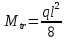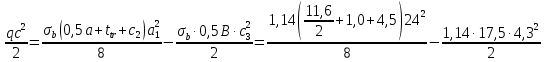

-

927,5 – 184.4 =743,1 кН·см².

Момент сопротивления траверсы W_tr = t_tr ⋅ 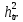/ 6 = 1,0·19² / 6 = 60,17 см³. Напряжение

σ = 743,1 / 60,17 = 12,35 кН/см² ˂ R_y = 24 кН/см², сечение траверсы удовлетворяет требованию прочности.

Список использованной литературы
1. Металлические конструкции. Под ред. Ю.И. Кудишина.-9-е изд.-М.: Издательский центр «Академия», 2007. – 688 с.

2. Металлические конструкции. Общий курс. Под общ. ред. Е.И. Беленя – 6-е изд. -М.: Стройиздат, 1986. – 560 с.

3. Бакиров К.К. Строительные конструкции II. Раздел «Металлические

конструкции». Учебное пособие. Аламты, КазГАСА 1996 г.

4. СНиП РК 5.04-23-2002. Стальные конструкции. - Астана, 2003. – 118 с.

5. Мандриков А.П. Примеры расчета металлических конструкций. –

М.: Стройиздат, 1991. – 431 с.