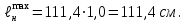жбк. 1 компоновка и выбор типа балочной клетки
 Скачать 1.91 Mb. Скачать 1.91 Mb.
|
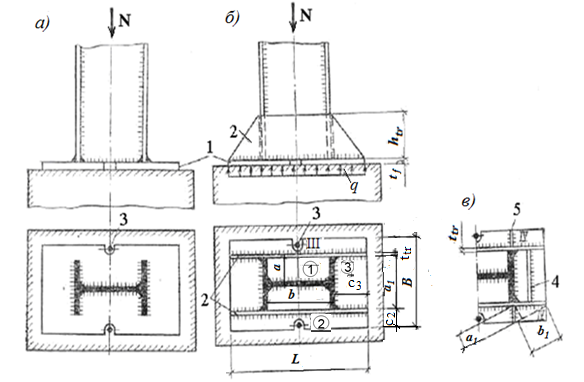
1 КОМПОНОВКА И ВЫБОР ТИПА БАЛОЧНОЙ КЛЕТКИ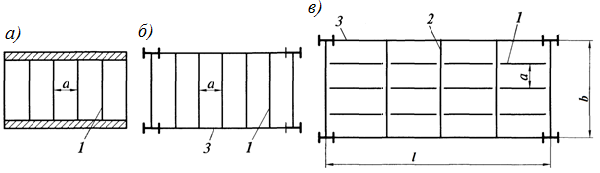 Типы балочных клеток: а – упрощенный; б – нормальный; в – усложненный; 1 – балки настила; 2 – вспомогательные балки; 3 – главные балки 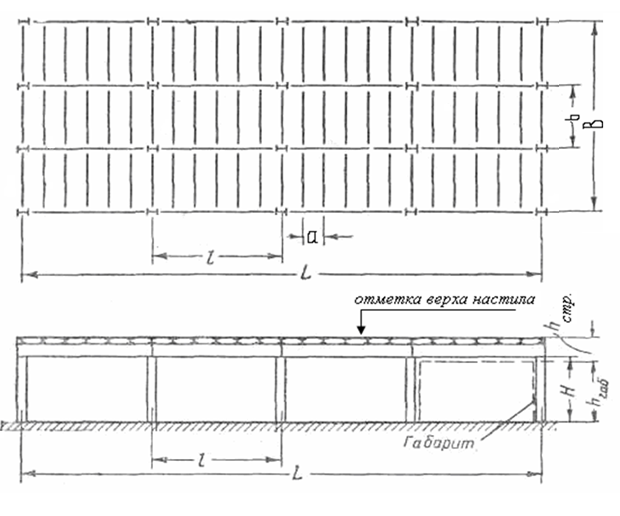 Генеральные размеры перекрытия балочной клетки Генеральные размеры перекрытия балочной клеткиРасстояние между балками настила «а» обычно принимают 0,6÷1,6 м при стальном настиле. При выборе расстояния между вспомогательными балками надо стремиться получить минимальное число балок, причем прокатных. Это расстояние обычно назначается в пределах 2÷5 м, и оно должно быть кратно пролету главной балки. 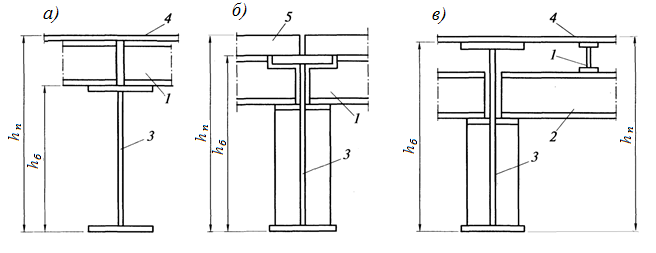 Сопряжения балока - этажное; б - в одном уровне; в – пониженное; hп – высота перекрытия; hб – высота главной балки; 1 – балки настила; 2 – вспомогательные балки; 3 – главные балки; 4 – стальной настил; 5 – железобетонный настил При нагрузке q 10 кН/м2 для настила следует использовать листы толщиной t = 6-8 мм; при 11 q 20 кН/м2 8-10 мм; при 21 q 30 кН/м2 10-12 мм; при q 30 кН/м2 12-14 мм. 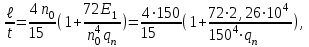 (1.1) (1.1)где n0 = ℓ / f = 150; qn – нормативная нагрузка на настил. 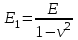 и ν – коэффициент Пуассона (для стали ν = 0,3) и ν – коэффициент Пуассона (для стали ν = 0,3)Прокатные балки можно использовать в конструкциях, требующих момент сопротивления W 13000 см3. Расчет на прочность прокатных балок, изгибаемых в одной из главных плоскостей, производится по формуле: 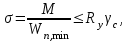 (1.2) (1.2)где М - максимальный изгибающий момент; Wn,min - минимальный момент сопротивления (нетто) сечения; Ry - расчетное сопротивление стали растяжению, сжатию, изгибу по пределу текучести; с - коэффициент условий работы. Поэтому требуемый момент сопротивления балки (нетто) можно определить по формуле: 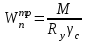 . (1.3) . (1.3)По сортаменту прокатных профилей находят номер профиля с W |
| Полезная нагрузка pn, кН/м2 | Толщина листа, мм |
| До 10 | 6 – 8 |
| 11 – 20 | 8 – 10 |
| 21 – 30 | 10 – 12 |
| > 31 | 12 – 14 |
При нагрузках, не превышающих 50 кН/м2, и предельном относительном прогибе fu/lн = 1/nо ≤ 1/150 прочность шарнирно закрепленного по краям стального настила всегда будет обеспечена и его рассчитывают только на жесткость.
Определяем вес настила, зная, что 1 м2 стального листа толщиной 10 мм весит 78,5 кг
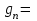 78,5·1,0 = 78,5 кг/м2
78,5·1,0 = 78,5 кг/м2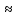 0,785 кН/см2.
0,785 кН/см2.Нормативная нагрузка на балку настила
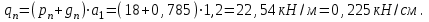
Расчетная нагрузка на балку настила
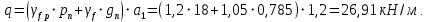
Расчетный изгибающий момент (при ℓ= b = 5 м)
Мmax=qℓ2/8 = 26,91· 52/8 = 84,09 кНм = 8409 кНсм
Требуемый момент сопротивления балки
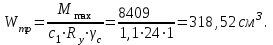
где с1 – коэффициент, учитывающий развитие пластических деформаций, равен 1,1
Ry – расчетное сопротивление стали, принимается в зависимости от класса стали (табл. 2).
γс – коэффициент условия работы стали, (табл. 3) СНиП РК 5.04-23-2002 Стальные конструкции, с.8
Таблица 2
Показатели сопротивлений сталей
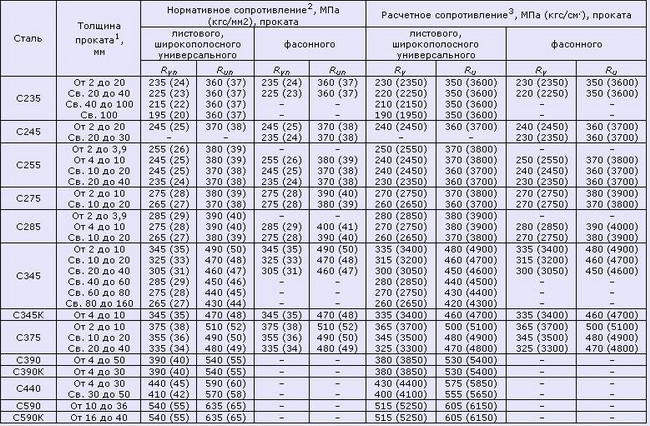
Таблица 3
Коэффициенты условий работы для металлических конструкций

Таблица 3
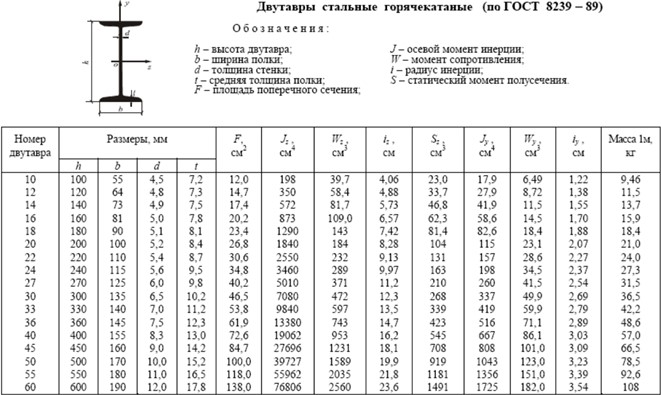
По сортаменту (табл. 3) принимаем двутавр №27 Wx=371 см3, g=31,5кг/м , Ix=5010 см4, b=125мм.
Проверяем только прогиб, так как W = 371 см3 > Wтр = 318,52 см3
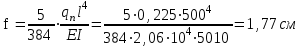
Проверяем условие жёсткости
1,77
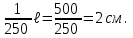
Определим фактический пролёт настила (расстояние между полками балок настила в свету)
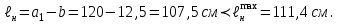
Принятое сечение балки удовлетворяет условиям прочности и прогиба. Проверку касательных напряжений прокатных балках при отсутствии ослабления опорных сечений обычно не производят, так как она легко удовлетворяется из-за относительно большей толщины стенок балок.
Общую устойчивость балок настила проверять не надо, так как их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним настилом.
Определяем расход металла на 1 м2 перекрытия
- настил
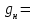 78,5·1=78,5 кг/м2
78,5·1=78,5 кг/м2- балка настила g/a1 = 31,5/1,2 = 26,25 кг/м2.
Весь расход металла составит 78,5+26,25= 104,75 кг/м2 = 1,05 кН/м2.
Вариант 2. Усложненный тип балочной клетки
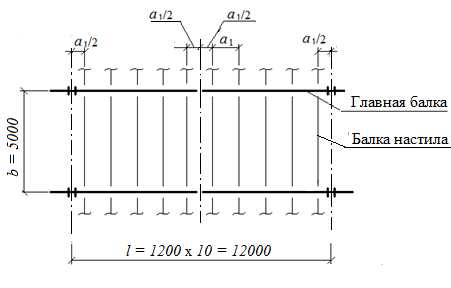
Определяем «n» количество шагов балок настила
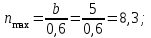
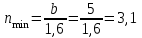
Принимаем n = 6 шт
Определяем а1длину шага балок настила
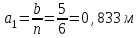
Расстояние между вспомогательными балками рекомендуется назначать в пределах 2-5 м. Определяем количество шагов вспомогательных балок
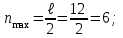
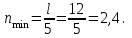
Принимаем n = 4, тогда расстояние между вспомогательными балками (шаг)
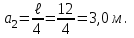

Рисунок 4.2 Усложнённый тип балочной клетки
Толщину настила принимаем такой же, как в первом варианте tн=10 мм. Тогда и нагрузка от настила останется прежней
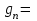 78,5·1,0=78,5 кг/м2=0,785 кН/м2.
78,5·1,0=78,5 кг/м2=0,785 кН/м2.Нормативная нагрузка на балку настила
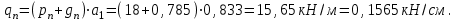
Расчетная нагрузка на балку настила
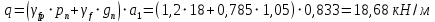
Расчетный изгибающий момент (при ℓ=а2=3,0 м)
Мmax=qℓ2/8 = 18,68·3,02/8 = 21,02 кН⋅м=2102 кН⋅см
Требуемый момент сопротивления балки (для стали С245 Ry = 240 МПа)
Wтр =
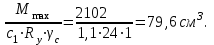
По сортаменту принимаем двутавр №16, имеющий: Wx=109см3, g = 15,9 кг/м, Ix=873см4, b=81мм.
Проверяем только прогиб, так как W = 109 см3> Wтр = 79,6 см3
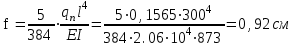 <300/250=1,2 см .
<300/250=1,2 см .Принятое сечение балки удовлетворяет условиям прочности и прогиба.
Нагрузка на вспомогательную балку от балок настила считаем равномерно распределенной, так как число балок не меньше 4. Определяем нормативную и расчётную нагрузку на вспомогательную балку
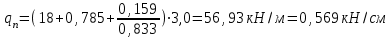
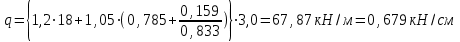
Определяем расчетный изгибающий момент и требуемый момент сопротивления
М= ql2/8=67,9·52/8=212,19кН·м=21219 кН·см;
Wтр.=М/(сх·Ry·
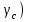 =21219/(1,1·24·1) =803,75см3.
=21219/(1,1·24·1) =803,75см3.Выбираем по сортаменту двутавр № 40, имеющий Wx = 953 см3,
Ix= 19062 см4, g = 57 кг/м, bf = 155 мм, tf = 13 мм, h = 400 мм.
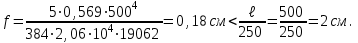
Проверяем общую устойчивость вспомогательных балок в середине пролета, в сечении с наибольшими нормальными напряжениями. Их сжатый пояс закреплен от поперечных смещений балками настила, которые вместе с приваренным к ним настилом образуют жесткий диск. В этом случае за расчетный пролет принимаем расстояние между балками настила ℓef = 83,3 см.
Общую устойчивость можно не проверять, если выполняется условие:
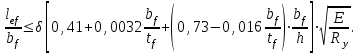
Проверим условия применения формулы:
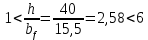 и
и 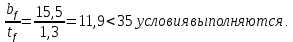 В сечении ℓ/2 τ = 0, следовательно
В сечении ℓ/2 τ = 0, следовательнос1 = с и δ =1- 0,7
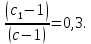
Подставим полученные значения
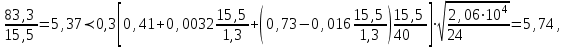
т.е. общую устойчивость балки можно не проверять.
Принятое сечение удовлетворяет требованиям прочности, устойчивости и прогиба.
По варианту 2 суммарный расход металла составляет
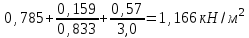
По расходу металла вариант №1 выгоднее, так как 1,05 кН/м2 <1,166кН/м2.
Компоновка и подбор сечения составной главной балки
Сечение составной главной балки подбираем по первому варианту компоновки балочной площадки. Балку проектируем из стали С 255, имеющей при толщине t ≤ 20 мм с Ry = 240 МПа и Rs = 0,58·Ry=139 МПа = 13,9кН/см2. Её предельный прогиб составляет f ≤ (1/400)ℓ.
Масса настила и балок настила g = 1,05 кН/см2, собственную массу балки принимаем ориентировочно в размере 1-2 % от нагрузки на неё. Максимально возможная строительная высота перекрытия по заданию hстр. = 1,6 м.
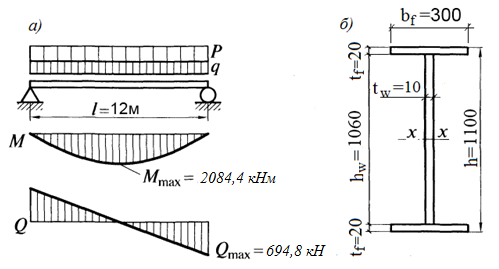
Рисунок 4.3 Расчетные схемы
а - расчётная схема главной балки; б – сечение балки
Определим нормативную и расчетную нагрузку на балку:
qn = 1,02(pn + gn)·b =1,02(18+1,05)·5=97,2 кН/м
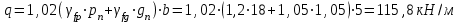
Определим расчетный изгибающий момент в середине пролета

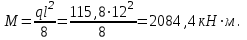
Поперечная сила на опоре
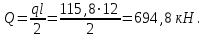
Главную балку рассчитываем с учетом развития пластических деформаций. Определяем требуемый момент сопротивления балки, первоначально принимая с1=с =1,1
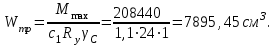
Определяем оптимальную высоту балки, предварительно задав высоту и толщину стенки
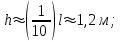
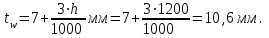
Сравнив с имеющимися толщинами проката листовой стали, принимаем толщину стенки 10 мм.
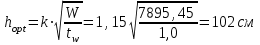
Минимальную высоту балки определяем по формуле:
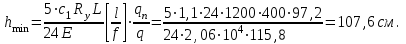
Строительную высоту балки определяем исходя из максимально возможной заданной высоты перекрытия и его конструкции:
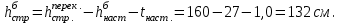
Сравнивая полученные высоты, принимаем высоту балки больше, чем hmin, близкой к hopt и кратной 100 мм h = 110 см.
Проверяем принятую толщину стенки балки:
- из условия прочности стенки балки на касательные напряжения при опирании с помощью опорного ребра, приваренного к торцу балки
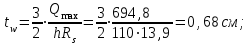
- из условия обеспечения местной устойчивости стенки балки без укрепления её продольным ребром жёсткости
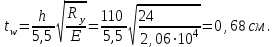
Сравнивая полученную расчетным путем толщину стенки с принятой (10 мм), приходим к выводу, что она удовлетворяет условию прочности на действия касательных напряжений и местной устойчивости.
Размеры горизонтальных поясных листов находят исходя из необходимой несущей способности балки. Для этого вычисляем требуемый момент инерции сечения балки
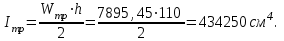
Находим момент инерции стенки балки, принимая толщину поясов tf = 2 см
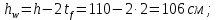
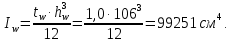
Момент инерции, приходящийся на поясные листы
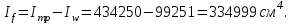
Момент инерции поясных листов балки относительно ее нейтральной оси
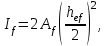
где Аf – площадь сечения пояса. Моментом инерции поясов относительно их собственной оси ввиду его малости пренебрегаем.
Отсюда получаем требуемую площадь сечения поясов балки:
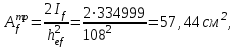
где hef = h – tf = 110 – 2 = 108 cм.
Принимаем пояса из универсальной стали bf x tf = 300×20 мм Af = 60 см2, для которой отношение bf/ h =300 / 1100=1 / 3,66 находится в пределах (1/3 – 1/5) рекомендуемого.
Уточняем принятый ранее коэффициент учета пластической работы «с» исходя из:
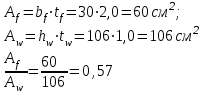
По табл.66 [4] уточняем коэффициент с = 1,11, который практически соответствует ранее принятому значению с = 1,1. Поэтому его оставляем без изменения.
Проверяем принятую ширину (свес) поясов в сечениях, работающих с учётом развития пластических деформаций, исходя из их местной устойчивости:
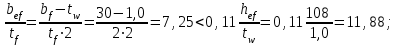
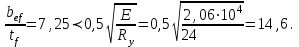
Проверяем несущую способность балки исходя из устойчивости стенки в области пластических деформаций балки в месте действия максимального момента, где
Q и τ = 0.
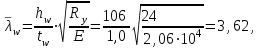
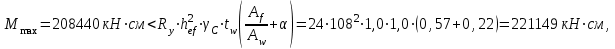
где α = 0,24 – 0,15·(τ/Rs
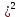 – 8,5·10-3(
– 8,5·10-3(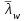 - 2,2)2 = 0,24-8,5·10-3·(3,62-2,2)2 = 0,22.
- 2,2)2 = 0,24-8,5·10-3·(3,62-2,2)2 = 0,22. Устойчивость стенки балки обеспечена.
Подобранное сечение балки проверяем на прочность. Для этого определяем момент инерции и момент сопротивление балки
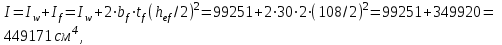
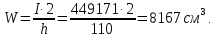
Наибольшее напряжение в балке:
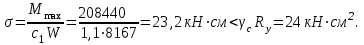
Подобранное сечение балки удовлетворяет условию прочности. Высота сечения балки принята больше минимальной, поэтому проверку прогиба балки делать не нужно.

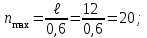
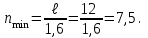
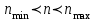 n =10 дана.
n =10 дана.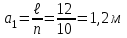
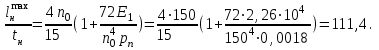
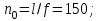
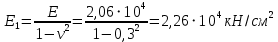 ,
,