кристаллка. 1. Кристаллическое состояние вещества. Признаки и основные свойства кристаллов
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
|
1. Кристаллическое состояние вещества. Признаки и основные свойства кристаллов. Кристаллическое состояние вещества характеризуется наличием дальнего порядка в расположении частиц (атомов, молекул, ионов), т.е. внутреннее упорядоченное строение. Твёрдое тело представляет собой кристалл или кристаллическое вещество, если при прохождении через него рентгеновских лучей происходит дифракция и видна ясная дифракционная картина. Основные свойства кристаллов: 1) Однородность – любые элементарные объёмы кристаллического вещества, одинаково ориентированные в пространстве, абсолютно одинаковы по всем физическим свойствам. 2) Анизотропность – физические свойства не одинаковы по не параллельным направлениям. 3) Самоогранение – любой обломок кристалла в соответствующей для его роста среде с течением времени покрывается характерными для данных кристаллов гранями. 2. Элементы симметрии кристаллических многогранников. Элементы симметрии – воображаемые геометрические образы, под действием которых повторяются части симметричных фигур. Элементы симметрии: 1) Центр инверсии (симметрии) – особая точка внутри фигуры, совпадающая с центром тяжести многогранника (C) 2) Поворотная ось (ось симметрии) – прямая линия, вокруг которой закономерно повторяются равные части фигур (Ln) !) Инверсионные оси – сочетание поворота вокруг оси вращения с отражением в центре симметрии Li1 = C Li2 = P Li3 = L3C Li4 = L2 Li6 = L3P (P перпендикулярна L3) 3) Плоскость зеркального отражения – делит фигуру на 2 зеркальные равные части Все элементы симметрии всегда проходят через центр тяжести многогранника (P) 3. Теоремы сложения элементов симметрии. Теорема Эйлера: если существуют 2 элемента симметрии, то обязательно присутствует третий, равнодействующий для первых двух. Т1: линия пересечения двух плоскостей – простая ось симметрии Следствие 1: если через ось симметрии проходит плоскость, то число проходящих через ось, равно порядку оси Т2: ось чётного порядка + центр симметрии = перпендикулярная плоскость Следствие 2: если есть центр симметрии, то сумма чётных осей = сумме плоскостей отражения Т3: две пересекающиеся оси дают третью равнодействующую ось, проходящую через точку их пересечения 4. Закон Стенона-Роме-Делиля. Гониометрический метод изучения формы кристаллов. Закон постоянства углов гласит, что углы между соответственными гранями и ребрами кристаллов одного и того же вещества постоянны Гониометрический метод: Основан на законе постоянства углов между соответствующими гранями. Для измерения углов используют прикладные и отражательные гониометры. 5. Сингонии. Характеристика сингоний по единичным направлениям. Сингония – группа видов симметрии с одним или несколькими сходными элементами симметрии. Низшая категория: Триклинная сингония – все направления единичные Моноклиннная сингония – много, но не все направления единичные Ромбическая сингония – три единичных направления Средняя категория (тригональная, тетрагональная и гексагональная сингонии): Одно единичное направление, совпадает с главной осью Высшая категория (кубическая сингония): Нет единичных направлений 6. Вывод видов симметрии низшей категории. Триклинная сингония: Примитивный – [ - (1)] Минимальный набор поворотных осей Добавляем центр – Центральный [Li1 = C ( 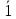 )] Поворотные оси + центр (здесь Li1) )] Поворотные оси + центр (здесь Li1)Моноклинная: Аксиальный – только L2 (2) Главная ось + | L2 Планальный – только P (m) Плоскости симметрии + поворотная ось Планаксиальный – L2 + C = P –> L2PC Аксиальный + центр Ромбическая: Аксиальный – 3L2 (222) Главная ось + | L2 Планальный – P + P = L2 (линия пересечения двух плоскостей – простая ось симметрии) –> L22P (mm2) Плоскости симметрии + поворотная ось Планаксиальный – к 3L2 добавим центр –> 3L23PC Аксиальный + центр 7. Вывод видов симметрии тетрагональной сингонии. Примитивный – только L4 (4) Минимальный набор поворотных осей Центральный – L4 + C = P –> L4PC Поворотные оси + центр Аксиальный – L44L2 Главная ось + | L2 Планальный – L44P Плоскости симметрии + поворотная ось Планаксиальный – L44L25PC Аксиальный + центр Инверсионно-примитивный – Li4 Только инверсионная ось Инверсионно-планальный – Li43L22P Инверсионно-примитивный + плоскость (Li4 = L2) 8. Вывод видов симметрии гексагональной сингонии. Примитивный – только L6 (6) Минимальный набор поворотных осей Центральный – L6 + C = P –> L6PC Поворотные оси + центр Аксиальный – L66L2 Главная ось + | L2 Планальный – L66P Плоскости симметрии + поворотная ось Планаксиальный – L66L27PC Аксиальный + центр Инверсионно-примитивный – Li6 Только инверсионная ось Инверсионно-планальный – Li63L23P Инверсионно-примитивный + плоскость (Li6 = L3P) 9. Вывод видов симметрии кубической сингонии. Примитивный – 4L33L2 Минимальный набор поворотных осей Центральный – 4L33L2 + C = 4L33L23PC Поворотные оси + центр Аксиальный – 3L44L36L2 Главная ось + | L2 Планальный – 4L33L26P = 3Li44L36P Плоскости симметрии + поворотная ось (Li4 = L2) Планаксиальный – 3L44L36L29PC Аксиальный + центр 10. Кристаллографические (стереографические) проекции элементов симметрии кристаллов. Те самые штуки, которые мы рисуем на проекциях  Проекция вертикальной оси симметрии попадет в центр круга проекции. Проекции горизонтальных осей симметрии являются диаметрами круга проекции 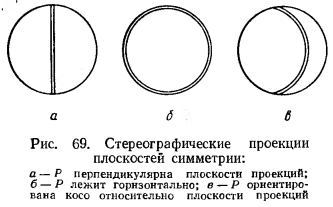 Проекция вертикальной плоскости симметрии является диаметром круга Проекция горизонтальной плоскости симметрии совпадает с кругом проекции 11. Кристаллографические (гномостереографические) проекции граней кристаллов. Эммм…. Крестик и нолик? 12. Простые формы кристаллов и комбинационные многогранники. Форма многогранника – совокупность всех его граней Простая форма – совокупность всех граней многогранника, которые связаны между собой элементами симметрии Закрытая простая форма – совокупность граней, полностью замыкающих заключённое между ними пространство. Открытая форма, соответственно, не замыкает. Открытые формы встречаются только в низшей и средней категории. Комбинационные многогранники – многогранники, содержащие грани нескольких простых форм 13. Простые формы низшей категории. Моноэдр, Пинакоид, Диэдр, Ромбическая призма, Ромбическая пирамида, Ромбическая дипирамида, Ромбический тетраэдр 14. Простые формы тригональной сингонии. Тригональная (+ Дитригональная ) призма, Тригональная (+Дитригональная) пирамида, Тригональная (+Дитригональная) дипирамида, Ромбоэдр, Тригональный скаленоэдр, Тригональный трапецоэдр 15. Простые формы тетрагональной сингонии. Тетрагональная (+ Дитетрагональная ) призма, Тетрагональная (+ Дитетрагональная ) пирамида, Тетрагональная (+ Дитетрагональная ) дипирамида, Тетрагональный тетраэдр, Тетрагональный скаленоэдр, Тетрагональный трапецоэдр 16. Простые формы гексагональной сингонии. Гексагональная (+ Дигексагональная ) призма, Гексагональная (+ Дигексагональная ) пирамида, Гексагональная (+ Дигексагональная ) дипирамида, Гексагональный трапецоэдр 17. Простые формы общего положения в кубической сингонии. Пентагонтритетраэдр, Гексатетраэдр, Дидодекаэдр, Пентагонтриоктаэдр, Гексаоктаэдр 18. Частные простые формы кристаллов кубической сингонии – производные куба. Тетрагексаэдр, Ромбододэкаэдр, Пентагондодекаэдр 19. Частные простые формы кристаллов кубической сингонии – производные октаэдра и тетраэдра. Тригонтритетраэдр, Тетрагонтритетраэдр, Тригонтриоктаэдр, Тетрагонтриоктаэдр 20. Разновидности простых форм. Энантиоморфизм. Закрытая простая форма – совокупность граней, полностью замыкающих заключённое между ними пространство. Открытая форма, соответственно, не замыкает. Открытые формы встречаются только в низшей и средней категории. Грань частного положения фиксирована какими-либо элементами симметрии (перпендикулярно, параллельно или равнонаклонно). Остальные положения граней – общие, т. е. не зафиксированные относительно элементов симметрии. Разновидности простых форм? Вершинные и рёберные? Энантиоморфизм -- Свойство некоторых кристаллов существовать в модификациях, являющихся зеркальными отражениями друг друга 21. Кристаллографические системы координат. Установка кристаллов низшей категории, выбор единичной грани. Кристаллографическая система координат. В общем случае косоугольная, начало координат в узле пространственной решетки, оси совпадают с рядами узлов решетки. При наличии элементов симметрии оси выбираются по осям симметрии или по нормалям к плоскостям симметрии Установка: 1. Центр тяжести кристалла совмещается с центром круга проекции 2. Кристаллы триклинной сингонии устанавливаются так, чтобы наибольшее число граней располагалось вертикально 3. Кристаллы моноклинной сингонии устанавливаются так, чтобы ось 2-го порядка располагалась горизонтально, а наибольшее число граней располагалось вертикально 4. Кристаллы ромбической сингонии устанавливаются так, чтобы одна из осей 2-го порядка располагалась вертикально Триклинная сингония — оси x,y,z вдоль ребер кристалла, ось z вдоль наиболее развитой зоны граней, углы между осями близки к 90о Моноклинная сингония — Ось y вдоль оси 2-го порядка или перпендикулярна к плоскости (слева направо), оси z вертикально параллельно ребрам наиболее развитой зоны, ось х параллельно ребру, направлена на наблюдателя Ромбическая сингония — Оси х y z — единичные направления вдоль осей 2-го порядка или перпендикулярно плоскостям симметрии Единичная грань пересекает все оси, или две двуединичные грани пересекают по две оси 22. Кристаллографические системы координат. Установка кристаллов тригональной и гексагональной сингоний, выбор единичной грани. Установка: Кристаллы средней категории устанавливаются так, чтобы ось высшего порядка располагалась вертикально Тригональная и гексагональная сингонии — Ось z вдоль главной оси 3-го или 6-го порядка Оси х, y, j — вдоль осей 2-го порядка или перпендикулярно плоскостям симметрии; Углы между горизонтальными осями 120о Единичная грань: та, которая пересекает все три оси или хотя бы две 23. Кристаллографические системы координат. Установка кристаллов тетрагональной и кубической сингоний, выбор единичной грани. Установка: Кристаллы кубической сингонии устанавливаются так, чтобы одна из осей 4-го или 2-го порядка располагалась вертикально Тетрагональная сингония — Ось z вдоль оси 4-го порядка Оси х y — вдоль осей 2-го порядка или перпендикулярно плоскостям симметрии; Оси взаимно перпендикулярны (ортогональная установка) Кубическая сингония — Оси х y z — по осям 4-го или 2-го порядка, оси взаимно перпендикулярны (ортогональная установка) Единичная грань: октаэдра или тетраэдра, даже если их нет в реальном кристалле 24. Обозначения видов симметрии по Браве и Герману-Могену. Поворотные оси симметрии обозначаются арабскими цифрами, соответствующими порядку оси: L1=1, L2=2, L3=3, L4=4, L6=6. Инверсионные оси обозначаются также арабскими цифрами, но с черточкой над цифрой, за исключением инверсионной оси второго порядка, для которой оставляют обозначение плоскости симметрии m: Li1=C=1̅, Li2=m, Li3=L3+C=3̅, Li4=4̅, Li6=L3+˔m=6̅. Плоскостям симметрии отдается предпочтение перед осями симметрии. При этом, указывая на какой-либо позиции плоскость m, имеем в виду, что соответствующему направлению параллелен перпендикуляр к m, т.е. инверсионная ось второго порядка. б. Если перпендикулярно простой оси симметрии имеется плоскость симметрии, такую комбинацию записывают в виде дроби: 2/m, 4/m, 6/m(комбинация 3/m соответствует Li3=3̅, которую и показывают в символе). Однако если ось симметрии в такой комбинации порождается другими элементами симметрии, показанными в символе, то в записи оставляют только обозначение плоскости симметрии, а обозначение оси не записывают. Например, для вида симметрии 3L23mCсимвол будет не 2/m2/m2/m, аmmm, так как оси второго порядка порождаются пересечениями плоскостей симметрии. в. В тригональной сингонии направления, параллельные горизонтальным координатным осям, и апофемные направления эквивалентны. Поэтому третья позиция всегда будет пустая. Так, для L33L2записываем 32, для L33m– 3m, хотя для соответствующих видов симметрии тетрагональной и гексагональной сингоний символы будут 422, 622, 4mm, 6mm. 25. Символы граней. Закон рациональности параметров Аюи. Расстояния от центра кристалла до граней пропорционально расстоянию между частицами на рёбрах. Индексы показывают наклоны граней к осям систем координат. Закон Аюи: Двойные отношения отрезков, отсекаемых любыми двумя гранями кристалла на координатных осях, равны отношению небольших целых чисел 26. Закон зон Вейса. Метод развития зон. Определение символов граней методом сложения Ось зоны – направление, параллельное всем рёбрам {h, k, l } – символы граней  Суммы соответствующих индексов двух непараллельных граней одной зоны равны индексам грани, лежащей между ними в этой же зоне 27. Символы направлений. Уравнение Вейса. Определение символов граней методом перекрестного умножения. Для определения символов направлений (осей зон, ребер) используют символы Вейса (без вычисления обратных отношений) Уравнение Вейса: hp + kq + lr = 0 ; hkl — символы грани, pqr — символы ребра  28. Предельные виды симметрии. Принцип Кюри. Ложные простые формы Предельных групп симметрии всего семь. Пять из них, c одной осью симметрии L ͚, являются предельными для видов симметрии средней категории, две группы с бесконечным количеством L͚ - предельными для видов симметрии высшей категории. Каждой группе можно сопоставить определенную геометрическую фигуру, имеющую те же элементы симметрии: 1 – L ͚, симметрия вращающегося кругового конуса. Вращение возможно как вправо, так и влево. Является предельной группой примитивных видов симметрии. 2 – L ͚ ∞m, симметрия неподвижного кругового конуса. Бесконечное количество продольных плоскостей симметрии возникает в соответствии с теоремой сложения 1б. Предельная группа планальных видов симметрии. 3 – L ͚ ˔mC, симметрия вращающегося кругового цилиндра. Вращение возможно как вправо, так и влево. Перпендикулярная оси плоскость симметрии возникает в соответствии с теоремой сложения 3б, так как ось L ͚ - в том числе и четная. Эта группа – предельная для центральных видов симметрии. 4 –L ͚ ∞L2, симметрия скрученного цилиндра (верхняя и нижняя грани цилиндра закручены в противоположные стороны). Бесконечное количество осей симметрии L2,перпендикулярных L ͚, возникает в соответствии с теоремой сложения 1а. Предельная группа аксиальных видов симметрии. 5 – L ͚ ∞L2∞mC, симметрия неподвижного кругового цилиндра. Получается из предыдущей группы добавлением центра инверсии, порождающего в соответствии с теоремой сложения 3б бесконечное количество плоскостей симметрии, перпендикулярных каждой L2, плюс выделенную плоскость симметрии, перпендикулярную L ͚. Группа, предельная для аксиально-центральных видов симметрии. 6 - ∞L ͚, симметрия шара, каждый радиус которого закручен в одну и ту же сторону (либо вправо, либо влево). Предельная группа для аксиального вида симметрии высшей категории. 7 - ∞L ͚ ∞mC, симметрия обычного шара. Получается из предыдущей группы добавлением центра инверсии, порождающего в соответствии с теоремой сложения 3б бесконечное количество плоскостей симметрии, перпендикулярных каждой из осей L͚. Группа, предельная для аксиально-центрального вида симметрии высшей категории. Принцип Кюри — второй важнейший фундаментальный постулат кристаллофизики, который позволяет определить изменение симметрии кристалла в результате воздействия на него. Этот принцип можно сформулировать следующим образом. Кристалл в результате внешнего воздействия изменяет свою симметрию так, что сохраняет лишь элементы симметрии, общие с элементами симметрии воздействия. 29. Плотнейшие упаковки в кристаллических структурах.       30. Типы химической связи в кристаллах. Структурные модели. Ковалентная, ионная, металлическая, ван-дер-ваальсова   Тетраэдр [SiO4 ] -4 – ковалентная связь Куб NaCl – ионная связь Размеры частиц в структуре: Каждая частица характеризуется атомным или ионным радиусом — сферой действия, внутрь которой не могут проникнуть посторонние атомы и ионы. Атомный или ионный радиус — минимальное расстояние, на которое центр сферы атома может приблизиться к поверхности сфер соседних атомов или ионов 31. Элементы симметрии кристаллических структур Немного не то: Узел — местоположение частицы в кристаллической структуре Ряд — совокупность узлов решетки, расположенных на прямой вдоль какого-либо направления Плоская сетка — совокупность узлов, расположенных в одной плоскости (эти узлы лежат на вершинах параллелограммов) Грани кристаллов отвечают сеткам, наиболее плотно покрытым частицами — с наибольшей ретикулярной плотностью Элементарная ячейка — минимальный 3-мерный фрагмент решетки, при перемещении которого с помощью трансляции пространство целиком будет заполнено. Элементарная ячейка обладает теми же элементами симметрии, что вся структура Трансляция — параметр кристаллической структуры — кратчайший параллельный перенос вдоль прямой (без поворота) до совпадения частиц Винтовая ось симметрии — линия, вокруг которой происходит вращение на определенный (элементарный) угол и перемещение вдоль этой линии на часть трансляции до совмещения фигуры с самой собой Плоскости скользящего отражения – совместное действие зеркальной плоскости и параллельной трансляции 32. Физические свойства кристаллов в зависимости от химических связей Ковалентная связь, обладающая строгой направленностью, резко ослабевает уже при незначительных смещениях атомов относительно друг друга. Поэтому кристаллы с ковалентным типом связи (Sb, Bi, As, se и др.) не проявляют способность к пластической деформации. Металлическая связь не имеет направленного характера и при смещении атомов относительно друг друга меняется слабо. Это определяет высокую степень пластичности металлов (ковкость). Наиболее ковкими являются те металлы, структуры которых построены по закону кубической плотнейшей упаковки, имеющей четыре направления плотноупакованных слоев. Менее ковки металлы с гексагональной плотнейшей упаковкой – с одним направлением плотнейших слоев. Так, среди полиморфных модификаций железа a-Fe и b-Fe ковкостью почти не обладают (решетка I типа), тогда как g-Fe с кубической плотнейшей упаковкой (гранецентрированная кубическая решетка) – ковкий металл как Cu, Pt, Au, Ag и др. Ионная связь не имеет направленного характера. Поэтому типичные ионные кристаллы (NaCl, CaF2, CaTe и др.) такие же хрупкие, как кристаллы с ковалентной связью. Но в то же время они обладают достаточно высокой пластичностью. Скольжение в них протекает по определенным кристаллографическим направлениям. Это объясняется тем, что в структуре кристалла можно выделить сетки (110), образованные либо одними ионами Na+, либо ионами Cl-. При пластической деформации одна плоская сетка передвигается относительно соседней таким образом, что ионы Na+ скользят вдоль ионов Cl-. Разноименность зарядов ионов в соседних сетках препятствует разрыву, и они остаются параллельными своему исходному положению. Скольжение вдоль этих слоев протекает при минимальном нарушении в расположении атомов и является наиболее легким. 33. Ячейки Браве.  34. Координационные числа. Пределы устойчивости структур и морфотропия. Координационное число – число ближайших к атому (иону) соседних атомов (ионов) в структуре Структура кристалла считается устойчивой лишь в том случае когда каждый ион соприкасается с ионом противоположного знака, при этом одинаково заряженные ионы удалены друг от друга. Предел устойчивости кристаллических структур определяется соотношением радиусов катиона и аниона в момент их касания. Например, соотношение радиусов катиона и аниона у октаэдра =0,41. Это означает что начиная с 0.41 и выше соединение с КЧ=6 будет устойчиво, при этом 0.41 – нижний предел устойчивости таких структур. Верхним пределом устойчивости с КЧ=6 является обратная величина 1:0.41=2.41 Морфотропия – закономерное изменение структуры при изменении состава в ряду сходных соединений – морфотропного ряда 35. Законы Грота и Гольдшмидта, распределение кристаллов по сингониям Закон Грота — чем проще химический состав вещества, тем выше симметрия его кристаллов. Закон Гольдшмидта: Общая распространенность химического элемента и его изотопов в природе зависит главным образом от свойств их атомных ядер, а поведение в природных геохимических процессах - от свойств наружной электронной оболочки их атомов. Распределение химических элементов в земной коре в связи с химическими и физическими свойствами атомов, а также с особенностями их поведения в кристаллической решетке.  36. Условия изоморфизма, изовалентный и гетеровалентный изоморфизм Условия изоморфизма: 1. Сохранение электронейтральности кристаллической решетки 2. Близость радиусов ионов, участвующих в замещении (разница не более 15 %) 3. Сходство в строении электронных оболочек ионов, участвующих в замещении Изовалентный изоморфизм – замещаются ионы с одинаковой валентностью Гетеровалентный изоморфизм – замещаются ионы с разной валентностью Пути выравнивания электростатического баланса вещества: а) дополнительное изоморфное замещение других элементов, баланс электрических зарядов соединения не меняется б) замещения неодинакового числа ионов в) компенсация зарядов дополнительными ионами 37. Степень совершенства изоморфизма Степень совершенства изоморфизма (при данных Т и Р) определяется близостью межатомных расстояний, состоянием химической связи и строением электронной оболочки атомов. 38. Полиморфизм и полиморфные модификации Полиморфизм – способность вещества существовать в различных кристаллических структурах, Полиморфные модификации — вещества одного состава с разными кристаллическими структурами — разные минералы (обозначаются греческими буквами α, β, γ и т. д.). 39. Основные типы полиморфных переходов Тип I: переходы со смещением атомов (деформационные) — обратимы и протекают быстро при определенных Р и Т. Тип II: переходы с разрывами связей между атомами (реконструктивные) — протекают медленно, это вызвано необходимостью разрыва связей в структуре и пространственного перераспределения атомов или ионов. 40. Получение и свойства рентгеновских лучей. Способы получения: Тормозное излучение – при торможении предварительно ускоренных электронов Характеристическое излучение – при переходе электронов с низкого уровня на более высокий в электронных оболочках атомов и молекул Синхронное излучение – при отклонении пучка летящих заряженных частиц в магнитном поле Свойства: Обладают оптическими свойствами: могут преломляться, отражаться, интерферировать, поляризоваться и дифрагировать (последнее – слабо выражено) Не несут эл.заряда Вызывают ионизацию газа Способны вызывать люминесценцию в ряде веществ, то есть свечение, видимое глазом 41. Закон (уравнение) Брегга-Вульфа.  42. Рентген-дифракционные методы исследования кристаллов. Рентген-дифракционные методы позволяют: 1. идентифицировать кристаллические фазы (CaCO3 / CaSO4) 2. различать полиморфные модификации (кальцит / арагонит CaCO3) 3. определять состав твердого раствора Рентген-дифрактометрические методы по объектам исследования разделяются на порошковые и монокристалльные 43. Формирование габитуса кристаллов. Закон Браве. 44. Типы дефектов кристаллов 45. Зарождение кристаллов. 46. Образование кристаллов из газовой фазы. 47. Образование кристаллов из расплавов. 48. Образования кристаллов из растворов. 49. Механизм роста кристаллов двумерными зародышами. 50. Дислокационный механизм роста кристаллов. 51. Механизм роста кристаллов трехмерными зародышами. 52. Захват примесей кристаллами при их росте. Зональность и секториальность. 53. Влияние температуры и примесей на форму кристаллов. 54. Влияние массопереноса на форму кристаллов. Скелетные кристаллы. 55. Блочность и двойникование кристаллов. Симметрия и морфология двойников. 56. Полярные и неполярные направления в кристаллах 57. Оптические свойства кристаллов (Линейная оптика) 58. Оптические свойства кристаллов (нелинейная оптика). 59. Магнитные свойства кристаллов. 60. Электрические свойства кристаллов. |
