КР. 1 линейные электрические цепи синусоидального тока 3 2 определение параметров четырехполюсника 6
 Скачать 262.03 Kb. Скачать 262.03 Kb.
|
СодержаниеВведение 2 1 ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА 3 2 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЧЕТЫРЕХПОЛЮСНИКА 6 3 ТРЕХФАЗНЫЕ ЦЕПИ 9 4 ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ТОКИ 12 5 ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ 17 6 ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ 20 7 УСТАНОВИВШИЕСЯ ПРОЦЕССЫ В ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 24 Заключение 29 Список литературы 30 ВведениеДанная курсовая работа включает в себя 7 заданий: Линейные электрические цепи синусоидального тока; Определение параметров четырехполюсника; Трехфазные цепи; Периодические несинусоидальные токи; Электрические фильтры; Переходные процессы в линейных электрических цепях; Установившиеся процессы в линии с распределенными параметрами. При выполнении этих заданий я должен освоить: Принципы расчета; Физические процессы, происходящие в данных заданиях; Принципы построения графиков и схем; Улучшить навыки работы в программе Mathcad. Данная курсовая работа ориентирована на подготовку к последующим этапам учебной деятельности, связанной с решением инженерных задач с использованием информационных систем и с приобретением навыков научного исследования. 1 ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКАДля электрической схемы выполнить следующее: На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух форматах: а) дифференциальной; б) символической. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей. По результатам, полученным в п. 2, определить показания ваттметра. Построить топографическую диаграмму, совмещенную с векторной диаграммой токов, потенциал точки а, указанной на схеме, принять равной нулю. Используя данные расчетов записать выражение для мгновенного значения тока i1. Построить график зависимости данной величины от ωt. 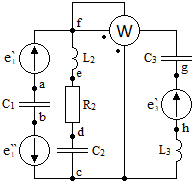 Рис. 1.1 – Схема задания Дано: 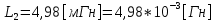 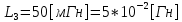 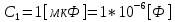 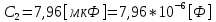 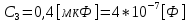 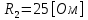 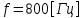 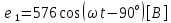 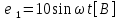 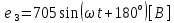 На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух форматах: 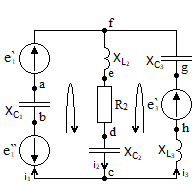 Рис. 1.2 – Схема для составления уравнений по законам Кирхгофа а) дифференциальной 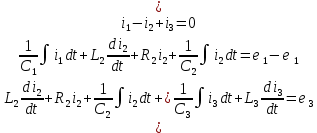 б) символической. 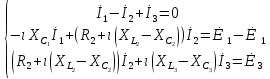 Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей. 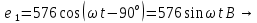 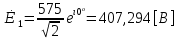 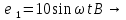 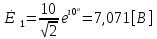 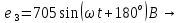 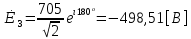 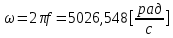 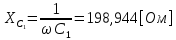 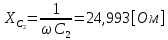 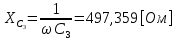 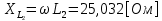 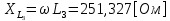 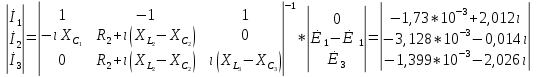 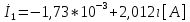 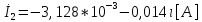 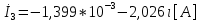 Построить топографическую диаграмму, совмещенную с векторной диаграммой токов, потенциал точки а, указанной на схеме, принять равной нулю. 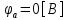 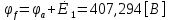 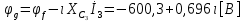 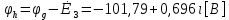 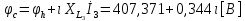 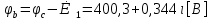  + +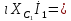 0 [В] 0 [В]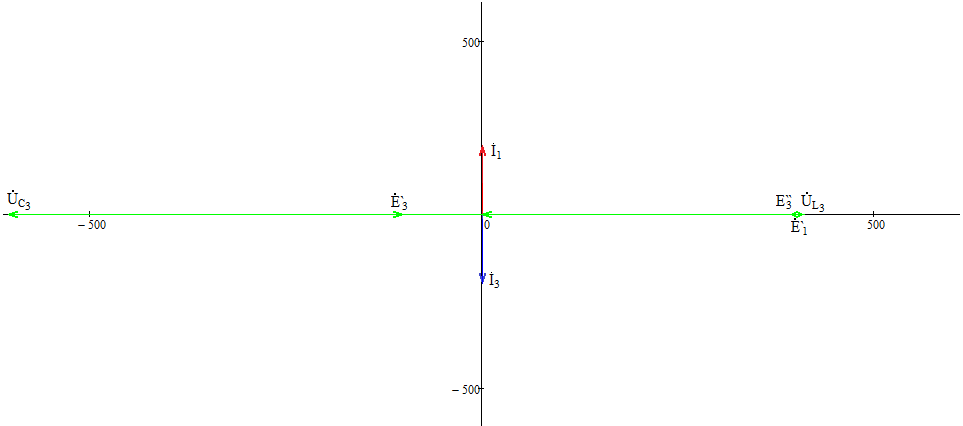 Рис. 1.3 – Топографическая диаграмма напряжений, совмещенная с векторной диаграммой токов По результатам, полученным в п. 2 и в п. 3, определить показания ваттметра. 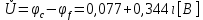 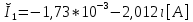 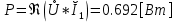 Используя данные расчетов записать выражение для мгновенного значения тока i1. Построить график зависимости данной величины от ωt. 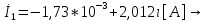 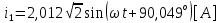 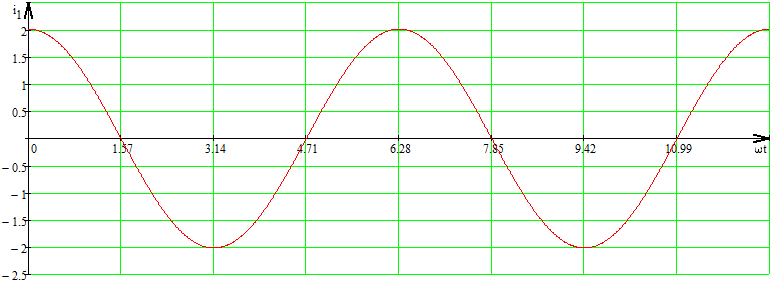 Рис. 1.4 – График зависимости i1 от ωt 2 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЧЕТЫРЕХПОЛЮСНИКАСхему задачи 1 представить как T-схему пассивного четырехполюсника. С этой целью все источники ЭДС в схеме закоротить, а левую (первую) и правую (третью) ветви разомкнуть. Разомкнутые зажимы левой ветви обозначить 1 – 1` и считать их входными, а разомкнутые зажимы правой части обозначить 2 – 2` и считать их выходными. Сопротивления левой ветви обозначить Z1, средней – Z3, правой Z2. Для полученной схемы составить уравнение четырехполюсника в матричной форме записи H. Записать формулы для элементов матриц сначала в общем виде, а затем в числовом.  Рис. 2.1 – Схема задания Дано: 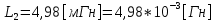 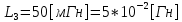 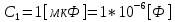 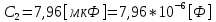 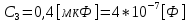 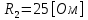 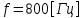 Схему задачи 1 представить как T-схему пассивного четырехполюсника. 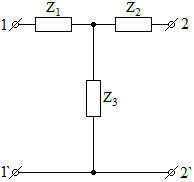 Рис. 2.2 – T-схема пассивного четырехполюсника С этой целью все источники ЭДС в схеме закоротить, а левую (первую) и правую (третью) ветви разомкнуть. Разомкнутые зажимы левой ветви обозначить 1 – 1` и считать их входными, а разомкнутые зажимы правой части обозначить 2 – 2` и считать их выходными. Сопротивления левой ветви обозначить Z1, средней – Z3, правой Z2. Угловая частота: 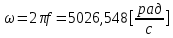 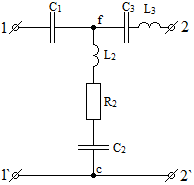 Рис. 2.3 – Схема четырехполюсника согласно варианту Сопротивление реактивных элементов в схеме: 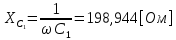 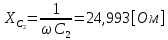 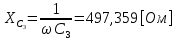 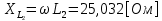 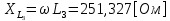 Тогда: 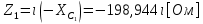 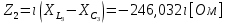 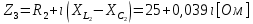 Для полученной схемы составить уравнение четырехполюсника в матричной форме записи H. Записать формулы для элементов матриц сначала в общем виде, а затем в числовом. Уравнение пассивного четырехполюсника в H-форме в общем виде: 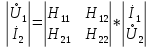 Для пассивного T-образного четырехполюсника коэффициенты основных уравнений равны: 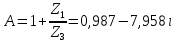 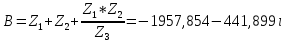 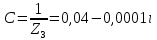 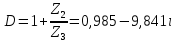 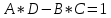 По формулам связи с основными уравнениями, коэффициенты в форме H: 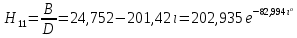 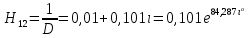 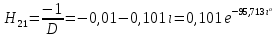 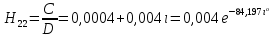 , где H11, H12, H21, H22 это H-параметры четырехполюсника. Уравнение пассивного четырехполюсника в H-форме в числовом виде: 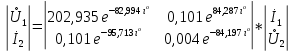 3 ТРЕХФАЗНЫЕ ЦЕПИНа рисунке 3.1 приведена схема трехфазной цепи. В ней имеется трехфазный генератор (создающий трехфазную симметричную систему ЭДС) и симметричная нагрузка. Действующие значение ЭДС фазы генератора EA, период T, параметры R1, L и C1 даны. Начальную фазу ЭДС EA принять нулевой. Требуется: рассчитать токи, построить векторную диаграмму токов и напряжений, определить мгновенное значение напряжения между заданными точками и подсчитать активную мощность трехфазной системы. 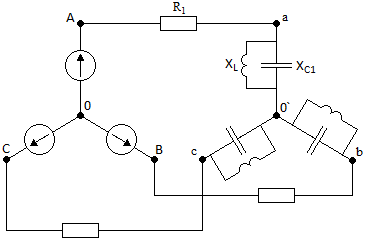 Рис. 3.1 – Схема задания 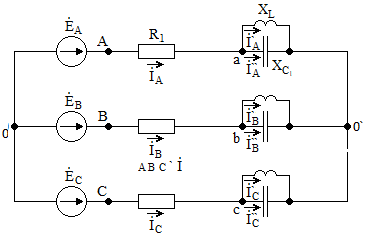 Рис. 3.2 – Преобразованная схема задания Дано: 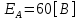 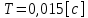 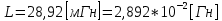 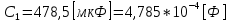 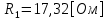 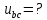 Расчет токов: Комплексные действующие значения ЭДС генератора равны: 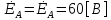 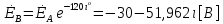 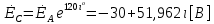 Угловая частота: 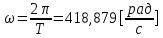 Сопротивления реактивных элементов: 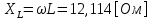 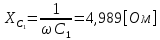 Линейное сопротивление: 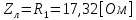 Фазное сопротивление: 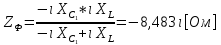 Т.к. линейные и фазные сопротивления всех фаз одинаковые, то линейные токи: 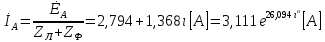 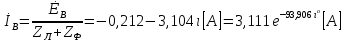 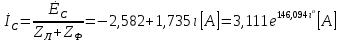 Проверка значений по 1-му закону Кирхгофа: 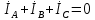 – верно. – верно.Остальные токи: 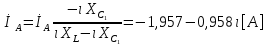 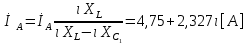 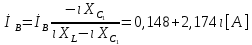 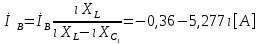 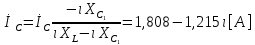 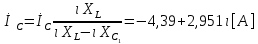 Потенциалы точек: 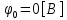 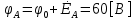 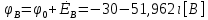 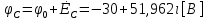 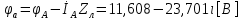 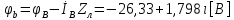 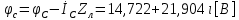 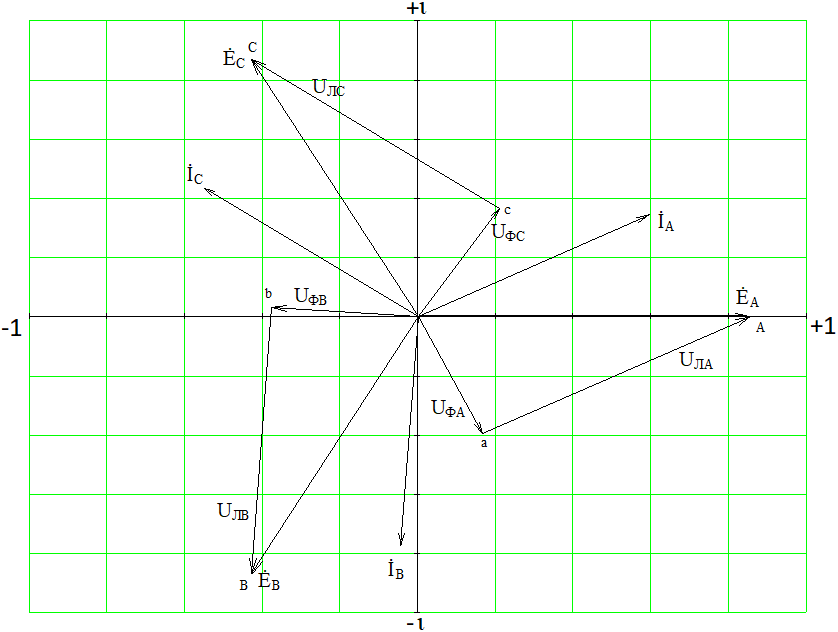 Рис. 3.3 – Топографическая диаграмма напряжений и векторная диаграмма токов Мгновенное значение напряжения между точками b и c: 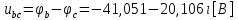 Мощность трехфазной системы: 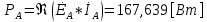 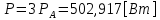 4 ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ТОКИНа рис. 4.1 дана схема, на вход которой воздействует периодическое напряжение u1(t) (график напряжения приведен на рис. 2.28). Схема нагружена на активное сопротивление нагрузки Rн. Численные значения напряжения Um, периода T, параметров схемы L, C и величина активного сопротивления нагрузки Rн даны. Требуется: Разложить напряжение u1(t) в ряд Фурье до 5-й гармоники включительно, используя табличные разложения, приведенные в учебниках, и пояснения, которые даны в указаниях к данной задаче. Обозначив сопротивления элементов схемы в общем виде как RН, ιXLи -ιXС, вывести формулу для передаточной функции K(ιω) четырехполюсника (рис. 4.1) 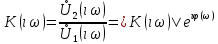 . Полученное выражение пригодно для каждой гармоники, только под ιXLи -ιXС следует понимать сопротивления для соответствующей гармоники. . Полученное выражение пригодно для каждой гармоники, только под ιXLи -ιXС следует понимать сопротивления для соответствующей гармоники.Используя формулу п. 2, определить комплексную амплитуду напряжения на выходе (на нагрузке) для следующих гармоник ряда Фурье: для 0-й, 1-й и 3-й гармоник. Записать мгновенное значение напряжения на нагрузке в виде ряда Фурье. Построить друг под другом линейчатые спектры входного (u1) и выходного (u2) напряжений. 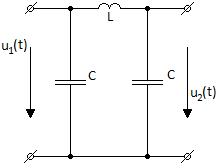 Рис.4.1 – Схема задания 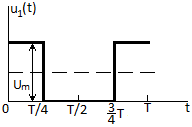 Рис. 4.2 – График входного напряжения Дано: 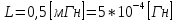 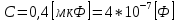 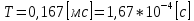 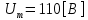 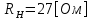 Разложить напряжение u1(t) в ряд Фурье до 5-й гармоники включительно, используя табличные разложения, приведенные в учебниках, и пояснения, которые даны в указаниях к данной задаче. 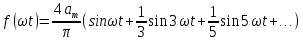 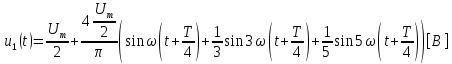 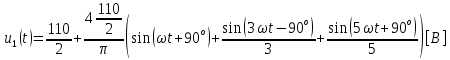 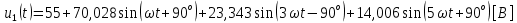 , где 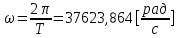 Обозначив сопротивления элементов схемы в общем виде как RН, ιXLи -ιXС, вывести формулу для передаточной функции K(ιω) четырехполюсника (рис. 4.1) 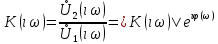 . . 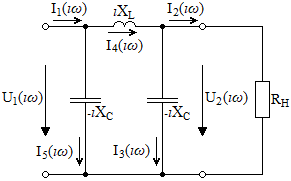 Рис. 4.3 – Схема нагруженного фильтра По закону Ома: 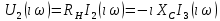 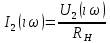 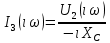 По 1-му закону Кирхгофа: 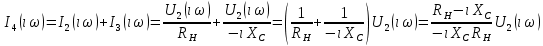 По закону Ома: 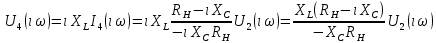 По 2-му закону Кирхгофа: 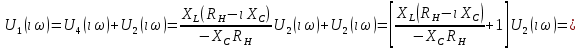 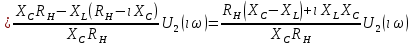 Тогда: 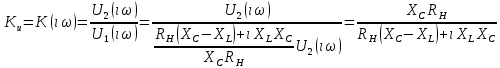 Используя формулу п. 2, определить комплексную амплитуду напряжения на выходе (на нагрузке) для следующих гармоник ряда Фурье: для 0-й, 1-й и 3-й гармоник. Расчет постоянной составляющей 0-й гармоники: Т.к. нагрузка RН включена последовательно с индуктивным элементом L, и параллельно с емкостным элементом C, то: 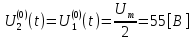 Расчет по 1-й гармонике: 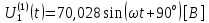 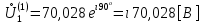 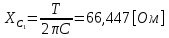 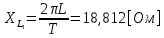 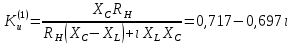 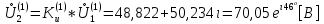 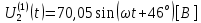 Расчет по 3-й гармонике: 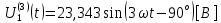 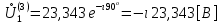 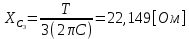 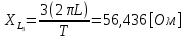 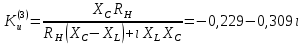 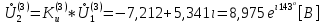 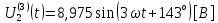 Расчет по 5-й гармонике: 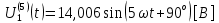 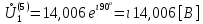 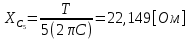 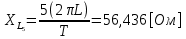 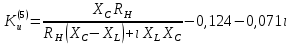 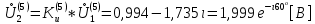 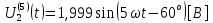 Записать мгновенное значение напряжения на нагрузке в виде ряда Фурье. 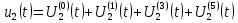 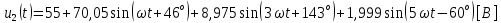 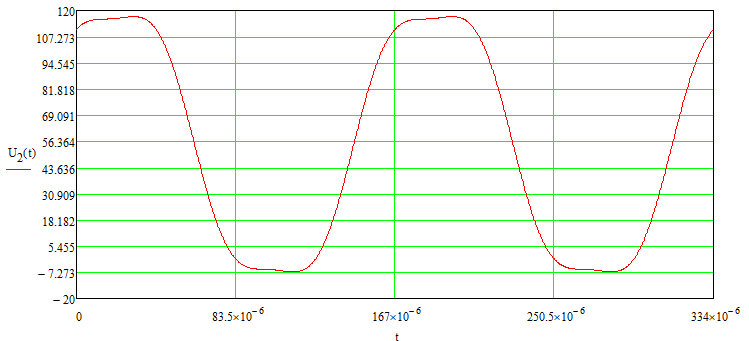 Рис. 4.4 – График выходного напряжения Построить друг под другом линейчатые спектры входного (u1) и выходного (u2) напряжений. 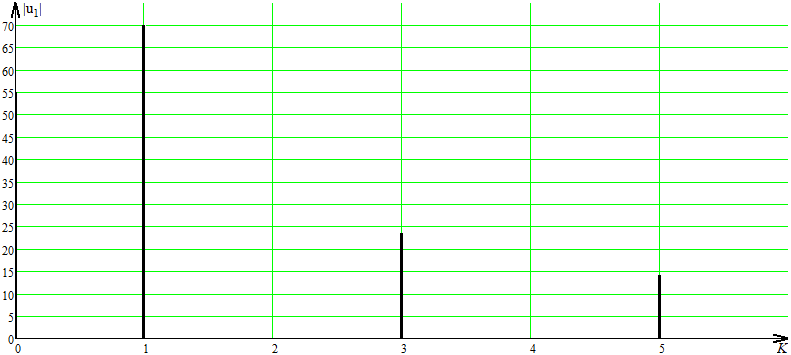 Рис. 4.5 – Линейчатый спектр входного (u1). 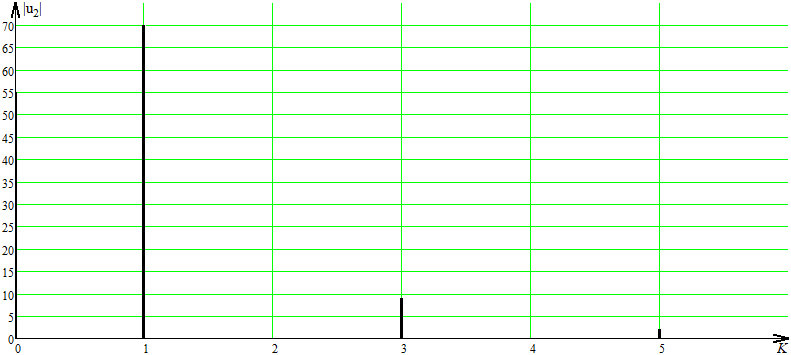 Рис. 4.6 – Линейчатый спектр выходного (u2). 5 ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫРассматривая схему 4.1, приведенную в условии задачи 4, как схему фильтра, работающего на согласованную нагрузку: Определить значения граничных частот полосы прозрачности фильтра (частот среза); Качественно построить зависимость характеристического сопротивления Zc, затухания a и сдвига по фазе b в функции частоты ω.  Рис. 5.1 – Схема задания Дано: 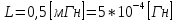 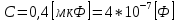 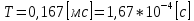 Определить значения граничных частот полосы прозрачности фильтра (частот среза). Связь коэффициентов четырехполюсника с параметрами П-образной схемы замещения определяется соотношениями: 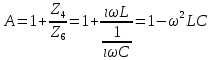 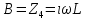 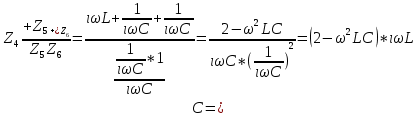 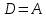 Из уравнений четырехполюсника, записанных с использованием гиперболических функций, следует: 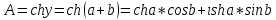 Однако 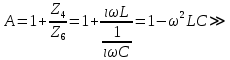 A – вещественная переменная, следовательно: A – вещественная переменная, следовательно: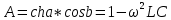 Поскольку в полосе пропускания частот коэффициент затухания а = 0, то: 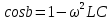 Так как пределы изменения cosb: 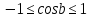 , то границы полосы пропускания определяются неравенством 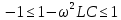 , которому удовлетворяют частоты, лежащие в диапазоне: , которому удовлетворяют частоты, лежащие в диапазоне: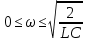 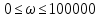 Полоса прозрачности: 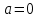 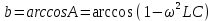 Таблица 1 – Коэффициент фазы в полосе прозрачности
Полоса затухания: 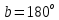 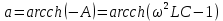 Таблица 2 – Коэффициент затухания в полосе затухания
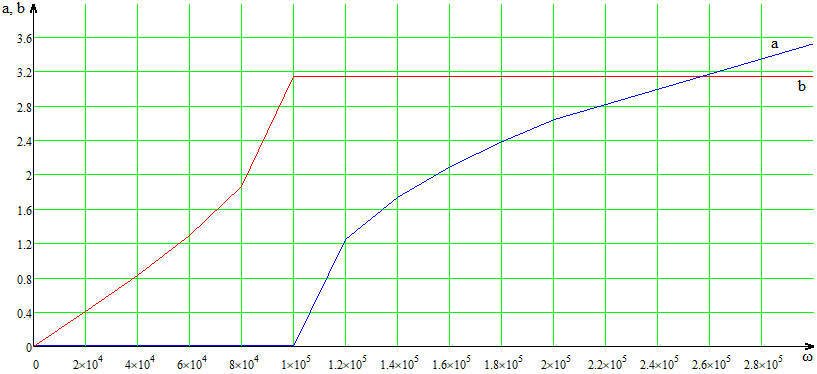 Рис. 5.2 – График зависимости затухания a и сдвига по фазе b в функции частоты ω Характеристическое сопротивление: 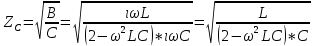 Таблица 3 – Характеристическое сопротивление
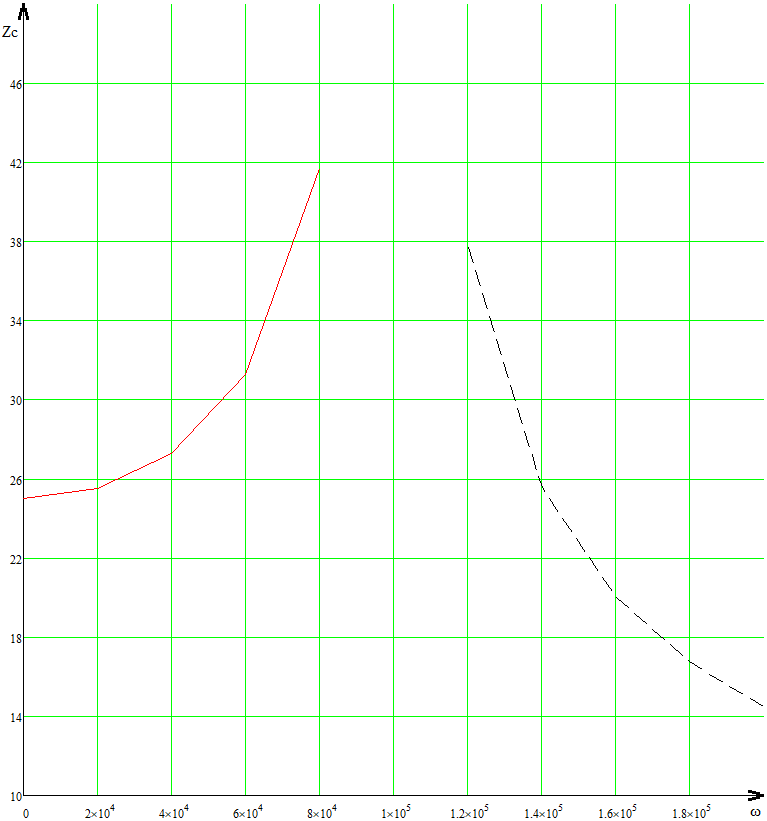 Рис. 5.3 – График зависимости характеристического сопротивления Zc в функции частоты ω 6 ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХДана электрическая цепь, в которой происходит коммутация (рис. 6.1). В цепи действует постоянная ЭДС E. Параметры цепи даны. Рассмотреть переходный процесс в цепи второго порядка, когда L2=0, т.е. участок a – b схемы закорочен, и когда C2 разомкнута. При вычерчивании схемы элементы L2 и C2 должны отсутствовать. Определить i3. Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения i3 в функции времени в интервале от t=0 до t=3/|p|min, где |p|min – меньший по модулю корень характеристического уравнения. 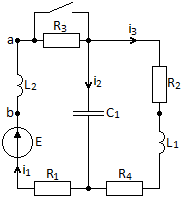 Рис. 6.1 – Схема задания Дано: 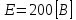 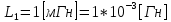 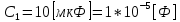 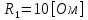 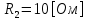 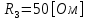 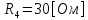 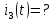 Определение независимых начальных условий: 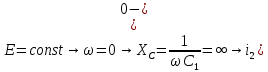 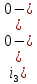 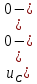 Определение принужденной составляющей: 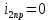 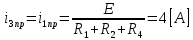 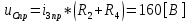 Свободная составляющая. Характеристическое уравнение: 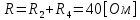 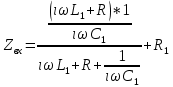 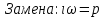 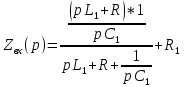  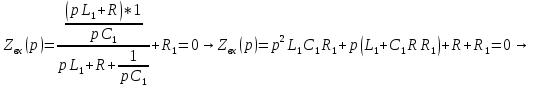 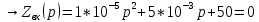 Корни квадратного уравнения: 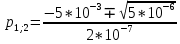 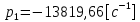 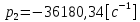 Получилось два действительных корня, не равных между собой, поэтому: 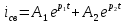 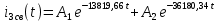 Дифференцирование уравнения по времени: 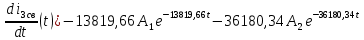 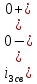 По второму закону Кирхгофа: 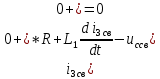 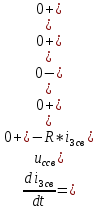 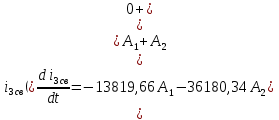 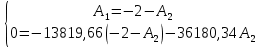 Отсюда 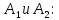 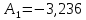 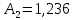 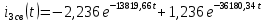 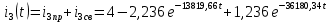 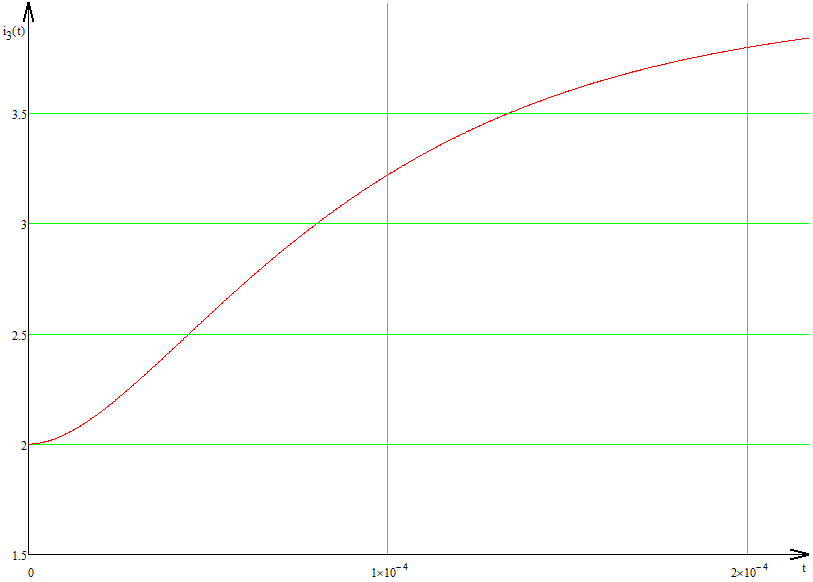 Рис. 6.2 – График изменения i3 в функции времени в интервале от t=0 до t=3/|p|min 7 УСТАНОВИВШИЕСЯ ПРОЦЕССЫ В ЛИНИИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИПо заданным параметрам линии (R0; L0; G0; C0), частоте f, длине линии l, комплексным значениям напряжения Ů2 и İ2 в конце линии, сопротивлению нагрузки ZH требуется: Рассчитать напряжение Ů1 и ток İ1 в начале линии, активную P и полную S мощности в начале и конце линии, а также КПД линии. Полагая, что линия п. 1 стала линией без потерь (R0=G0=0), а нагрузка на конце линии стала активной и равной модулю комплексной нагрузки в п. 1, определить напряжение Ů1 и ток İ1 в начале линии, а также длину электромагнитной волны λ. Для линии без потерь п. 2 построить график распределения действующего значения напряжения вдоль линии функции координаты y. 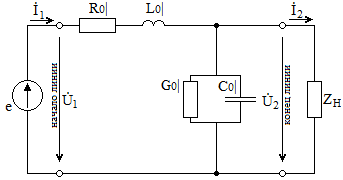 Рис. 7.1 – Схема задания Дано: 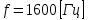 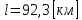 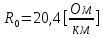 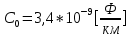 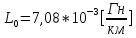 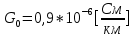 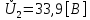 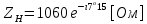 Рассчитать напряжение Ů1 и ток İ1 в начале линии, активную P и полную S мощности в начале и конце линии, а также КПД линии. Угловая частота колебаний источника ЭДС: 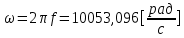 Продольное комплексное сопротивление на единицу длины одной линии: 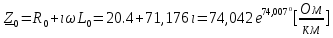 Поперечная комплексная проводимость на единицу длины одной линии: 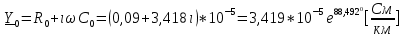 Примем: 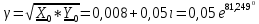 Отсюда: 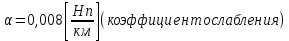 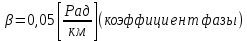 Характеристическое сопротивление линии: 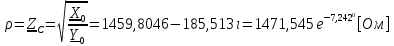 Напряжение и ток в начале линии (x = l): 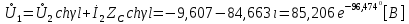 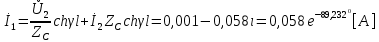 Полная 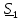 мощность в начале линии: мощность в начале линии: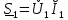 , где , где 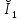 – сопряженный комплекс тока – сопряженный комплекс тока 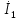 : :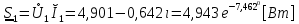 Следовательно, активная мощность в начале линии: 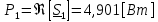 Полная 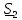 мощность в начале линии: мощность в начале линии: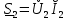 , где , где 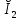 – сопряженный комплекс тока – сопряженный комплекс тока 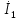 : :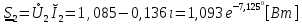 Следовательно, активная мощность в начале линии: 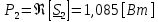 КПД линии: 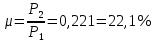 Полагая, что линия п. 1 стала линией без потерь (R0=G0=0), а нагрузка на конце линии стала активной и равной модулю комплексной нагрузки в п. 1, определить напряжение Ů1 и ток İ1 в начале линии, а также длину электромагнитной волны λ. Для линии без потерь: 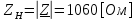 Такая линия характеризуется волновым сопротивлением: 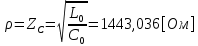 И коэффициентом распространения: 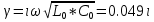 Волновое сопротивление линии без потерь является активным и не зависит от частоты. Коэффициент распространения определяется только коэффициентом фазы: 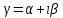 , где: 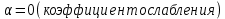 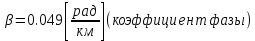 В установившемся режиме уравнения линии без потерь от показательной формы преобразуются к уравнениям в круговых тригонометрических функциях: 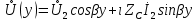 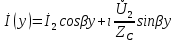 Напряжение и ток в начале линии (x = l): 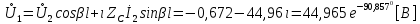 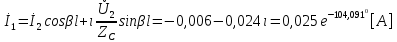 Длина электромагнитной волны: 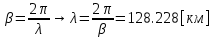 Для линии без потерь п. 2 построить график распределения действующего значения напряжения вдоль линии функции координаты y. 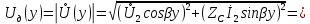   Рис. 7.2 – График распределения действующего значения напряжения вдоль линии функции координаты y ЗаключениеВ данной курсовой работе были выполнены все стоящие передо мной задания, которые помогли мне освоить: Принципы расчета; Физические процессы, происходящие в данных заданиях; Принципы построения графиков и схем; Улучшить навыки работы в программе Mathcad. Выполнив курсовую работу, я считаю, что готов к следующему этапу обучения по своей специальности. Список литературыТеоретические основы электротехники. Электрические цепи. Л. А. Бессонов 1996г. Москва Теоретические основы электротехники. Методические указания и контрольные задания. Л.А. Бессонов 2003г. Москва |
