Математическое описание. 1. Математическое описание. 1. Математическое описание непрерывных систем на макроуровне 1 Структура математического описания систем
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
1-4. Уравнения линейных систем10 . Полная система уравнений Уравнения на основе матриц П и Г. Топологические уравнения схемы можно получить на основании ее полюсного графа, выбор некоторого дерева в котором определяет совокупность главных сечений и главных контуров графа. Рассмотрение этих топологических структур дает возможность определить матрицу главных сечений Π и матрицу главных контуров Γ полюсного графа, что позволяет сформировать уравнения равновесия схемы Π I = 0 и Γ U = 0, где I, U – векторы токовых и потенциальных переменных компонентов схемы. Выделяя в этих векторах переменные y-полюсов и z-полюсов и разделяя соответствующим образом на блоки матрицы главных сечений Π и главных контуров Γ, можно записать топологические уравнения в виде:
Объединяя компонентные уравнения
(32) с уравнениями схемных связей (30) и (31), получим
Построенное уравнение описывает схему в координатном базисе, который включат в себя все потенциальные и токовые переменные компонентов схемы. Поскольку общее число таких переменных в реальных схемах чрезвычайно велико, то, несмотря на крайнюю простоту построения математического описания, практическое применение такого координатного базиса можно рекомендовать только для простейших задач. К отрицательным свойствам данной системы уравнений относится большое число неизвестных, равное всем напряжениям и токам. Уравнения на основе матрицы A. Полная система уравнений на основе матрицы А получается путём объединения компонентных уравнений и следующих соотношений: AI = 0 => 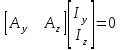 => => 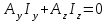 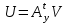 => => 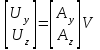 Полученная таким образом система будет выглядеть так:
Число переменных данной системы равно удвоенному числу полюсов плюс число узловых потенциалов 20. Минимально-мерный базис Наиболее эффективно задачу снижения числа переменных в уравнениях схемы можно решить путем перехода к координатному базису с вырождением части токовых и потенциальных переменных который часто называют минимально-мерным базисом, так здесь обеспечивается минимально-возможная размерность описания моделируемой схемы. Переход к такому базису оказывается возможным, если установить определенную иерархию в выборе ветвей дерева полюсного графа схемы. Согласно этой иерархии сначала в дерево включается максимально возможное число ветвей, отображающих переменные y-полюсов, а затем дерево дополняется необходимым количеством ветвей, отображающих z-полюсы. При выборе дерева согласно такой иерархии в графе вырождаются главные сечения, образованные z-ветвями дерева и главные контуры, образованные у-ветвями дополнения дерева, т.е. его z-связями. При этом уравнения равновесия схемы Π I = 0 и Γ U = 0 принимают вид:
Эти уравнения можно записать в виде Tp P + Tq Q = 0, (33) Q = Tpt X, (34) где
Вектор базисных переменных X определяется выражением
X = Решая уравнения равновесия (33), (34) совместно с объединенным компонентным уравнением P = Wм0Q + Sм0 (35) и исключая векторы P , Q, получим уравнение схемы в минимально-мерном базисе W0 X + S0 = 0 (36) где W0 = Tp Wм0Tpt + Tx , S0 = Tp Sм0 Здесь
Wм0= Sм0=
Отметим, что при вычислении матрицы Tx= Tq Tpt использовано фундаментальное соотношение между топологическими матрицами Γ Πt = 0, откуда следует соотношение Γzy Πyyt= – (Πyz Γzzt)t В развернутой форме уравнение (36) записываются в виде
|
