Математическое описание. 1. Математическое описание. 1. Математическое описание непрерывных систем на макроуровне 1 Структура математического описания систем
 Скачать 0.56 Mb.
|
1-3. Топологические уравнения10 . Полюсные графы и топологические матрицы Основные определения. Топологию (конфигурацию) схемы удобно задавать в виде направленного графа. Полюсный граф G многополюсного компонента – совокупность вершин, сопоставленных полюсам многополюсника и совокупность ветвей, сопоставленных выбранной системе отсчёта параллельных переменных многополюсника. Потенциальный полюсный граф многополюсника Gu – граф, ветви которого ориентированы в соответствии с выбранной ориентацией параллельных переменных многополюсника. Токовый граф многополюсника GI – граф Gu, ветви которого ориентированы противоположно. Потенциальный полюсный граф схемы – объединение потенциальных графов многополюсных элементов. Токовый граф схемы – объединение токовых графов многополюсных элементов. 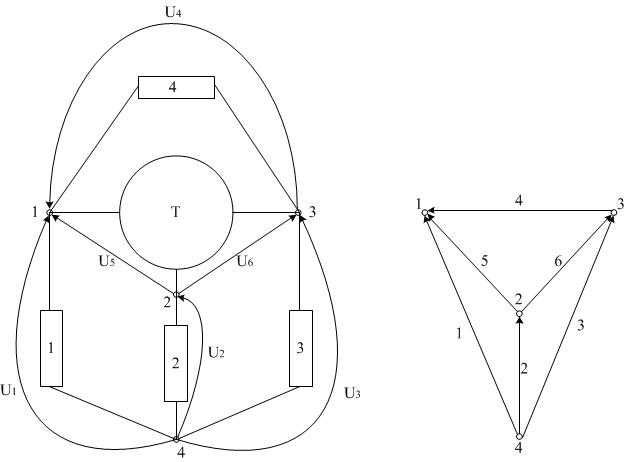 Пример схемы и ее потенциального полюсного графа Матрица инциденции (связи) A – матрица, строки которой соответствуют вершинам полюсного графа схемы, а столбцы – ветвям полюсного графа. aij = 1, если j-ая ветвь потенциального графа заходит в i-й узел; aij = -1, если j-ая ветвь потенциального графа выходит из i-ого узла; aij = 0, если j-ая ветвь не инцидентна i-ому узлу; Таким образом для многополюсника, изображенного на рисунке, можно построить полную матрицу инциденций  .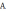
A= Данная матрица избыточна, поэтому вводят сокращённую матрицу A, путём исключения одной из строк:
A= Дерево графа – топологическая структура, включающая все вершины графа и совокупность ветвей касающаяся всех вершин графа и не образующую замкнутых контуров. Дополнение дерева – совокупность ветвей графа, которая не вошла в его дерево. Дерево графа и его дополнение для приведённой выше схемы изображено на рисунке, где ветви дерева изображены сплошными, а ветви дополнения дерева (связи) – пунктирными линиями. 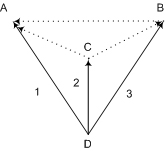 Главный контур – замкнутый контур графа, который содержит единственную связь и произвольное число ветвей графа. Матрица главных контуров Г – матрица, строки которой соответствуют связям, а столбцы – всем ветвям графа. Г = [ ij ] ij = + 1, если в i-ый контур, образованный i-ой связью, j-ая ветвь входит согласно; ij = – 1, если в i-ый контур, образованный i-ой связью, j-ая ветвь входит встречно; ij = 0, если в i-я связь и j-ая ветвь не входят ни в один контур. Таким образом для многополюсника, изображенного на рисунке, можно построить матрицу главных контуров
Г= Главное сечение – поперечное сечение графа, включающее в себя единственную ветвь дерева и произвольное число ветвей графа. Матрица главных сечений П – матрица, строки которой соответствуют ветвям дерева, а столбцы – ветвям графа. П = [ ij ] ij = + 1, если в i-ом сечении, образованном i-ой ветвью дерева, j-ая ветвь графа входит согласно с i-ой ветвью дерева; ij = – 1, если в i-ом сечении, образованном i-ой ветвью дерева, j-ая ветвь графа входит противоположно с i-ой ветвью дерева; ij = 0, если в i-я и j-ая ветви не входят в одно сечение. Таким образом для многополюсника, изображенного на рисунке, можно построить матрицу главных сечений
П = Фундаментальное свойство топологических матриц. Обе  матрицы П и Г могут быть записаны в нормализованной форме, когда сначала идут ветви дерева, а потом ветви связей:П = [ 1 | ] (14) Г = [ | 1 ] (15) Тогда имеют место равенства: ПГT = 0 (16) ГПT = 0 (17) Подставляя в (16) значения П и ГT получим [ 1 | ][ | 1 ]Т =0. Или T + = 0, откуда следует = – T и = – Т. Таким образом, достаточно иметь в распоряжении только одну из топологических матриц, на основании которой можно построить другую топологическую матрицу. Взаимосвязь матриц А, П и Г выражается следующими соотношениями: АГТ = 0 (18) П = Ад-1А (19) 20. Топологические и координатные уравнения. Уравнения равновесия. Вторая группа уравнений, входящая в математическое описание системы, образует уравнения равновесия. Уравнения равновесия составляются на основе рассмотрения некоторых топологических образов, содержащихся в полюсных графах системы. В общем случае такими топологическими образами являются системы независимых контуров и системы независимых сечений. Для таких контуров могут быть составлены уравнения равновесия (баланса) параллельных переменных и уравнения равновесия (баланса) последовательных переменных. Применительно к электротехническим системам уравнениями равновесия параллельных переменных являются уравнения Кирхгофа для напряжений в независимых контурах. Аналогично, уравнениями равновесия последовательных переменных для таких систем являются уравнения Кирхгофа для токов в независимых сечениях (узлах). В таблице приведены условия равновесия параллельных и последовательных переменных для различных физических систем.
Топологические уравнения. Запишем 1-й закон Кирхгофа, путём составления уравнения токов относительно i-ой строки матрицы П: 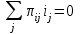 (20)Записав эти уравнения в матричной форме получим: П I = 0 (21) Аналогично запишем 2-й закон Кирхгофа: 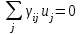 (22)Записав эти уравнения в матричной форме, получим: Г U = 0 (23) Координатные уравнения. Представим матрицу П в нормализованной форме и запишем уравнения (21) в структурированном виде [ 1 | ] 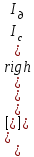 =0, или Iд + Iс =0. Отсюда следует Iд = – Iс, или Iд = T Iс (24) Дополним это уравнение тривиальным уравнением Iс = Iс (25) Объединим (24) и (25) в одно матричное уравнение, что дает 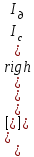= 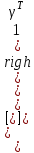Iс = ГT Iс Таким образом, получаем координатное уравнение I=ГTIс(26) Аналогичным образом на основании уравнения Г U = 0 нетрудно получить второе координатное уравнение U = П TUд (27) Смешанные уравнения на основе матрицы инциденций Выберем в схеме лагранжево дерево, что обеспечивает справедливость выражения П =A. При этом в выражении (27) вектор Uд = V , где V – вектор узловых потенциалов, и уравнения Кирхгофа (21) и (27) в матричной форме запишутся в виде A I = 0(28) U = A TV(29) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||