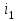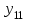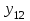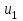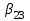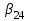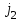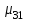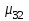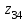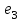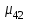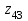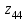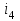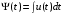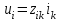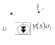Математическое описание. 1. Математическое описание. 1. Математическое описание непрерывных систем на макроуровне 1 Структура математического описания систем
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
1. Математическое описание непрерывных систем на макроуровне1-1. Структура математического описания системВ общем случае непрерывная система содержит некоторое количество многополюсных компонентов, связанных между собой.  Для такой схемы можно записать следующие уравнения: а) компонентные уравнения б) уравнения схемных связей (топологические уравнения) Совместное решение компонентных уравнения уравнений и уравнений схемных связей позволяет получить математическое описание схемы, которое в матричной форме может быть записано в виде WX+S=0 где W-матрица схемы X- вектор переменных S – вектор задающих внешних воздействий 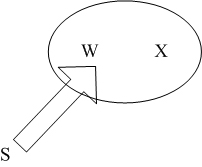 1-2. Компонентные уравнения10 . Линейный (линеаризованный) многополюсник Общая структура (n+1)- полюснника и 2n- полюсника приведена на рисунке  Для полюсов (n+1)-полюсника полюсное напряжение отсчитывается относительно (n+1)-го базисного узла. Полюса 2n-полюсника образуют так называемые порты, для которых можно выделить пару полюсов, относительно одного из которых отсчитывается полюсное напряжение каждого порта. Отличительной особенностью порта является равенство входного и выходного тока в соответствующей паре полюсов. Типичным примером порта является обмотка трансформатора, другим примером порта может служить вход дифференциального каскада на биполярных транзисторах, эмиттеры которых подключены к общему источнику тока. Будем полагать, что для каждого многополюсника зависимость между двумя переменными может быть записана уравнениями  , определяющими в явной форме для каждого полюса одну из полюсных переменных. Переменная , определяющими в явной форме для каждого полюса одну из полюсных переменных. Переменная  в общем случае может быть как последовательной, так и параллельной переменной. В зависимости от характера переменой в общем случае может быть как последовательной, так и параллельной переменной. В зависимости от характера переменой  все полюса многополюсников могут быть разделены на две группы: группу y-полюсов и группу z-полюсов. Группой y-полюсов обычно называются такие полюса, для которых зависимая переменная все полюса многополюсников могут быть разделены на две группы: группу y-полюсов и группу z-полюсов. Группой y-полюсов обычно называются такие полюса, для которых зависимая переменная  является переменной последовательного типа является переменной последовательного типа 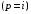 , а группой z-полюсов – полюса, для которых зависимая переменная , а группой z-полюсов – полюса, для которых зависимая переменная  является переменной параллельного типа. является переменной параллельного типа. Тогда для любого полюса, входящего в группу y-полюсов, полюсное уравнение может быть представлено в виде:  (1) (1)Аналогично, для любого полюса, входящего в группу z-полюсов, полосное уравнение может быть представлено в виде: 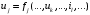 (2). (2).Проводя линеаризацию этих уравнений путем разложения их в ряд Тейлора в некоторой точке, можно представить уравнения (1) и (2) в виде:  , (3) , (3) . (4) . (4)Введем для линеаризованных неавтономных параметров обозначения  , ,  , , 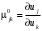 , , 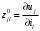 . .Кроме того, введем обозначения для автономных параметров y и z- полюсов 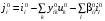 , , . .Тогда линеаризованные уравнения (3) и (4) могут быть записаны в виде  , (5) , (5)  . (6) . (6)В  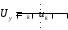 ведем, далее, векторы полюсных переменных y-полюсов ведем, далее, векторы полюсных переменных y-полюсовА  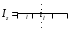 налогично, введем векторы полюсных переменных z-полюсов налогично, введем векторы полюсных переменных z-полюсов Кроме того, введем обозначения для матриц параметров многополюсников: Yм0=   , Bм0 = , Bм0 =  , Jм0 = , Jм0 =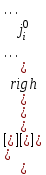 Mм0 = 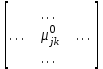 ,Zм0 = ,Zм0 = ,Eм0 = ,Eм0 = 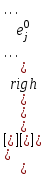 Тогда линеаризованные уравнения (5) и (6) можно записать в матричной форме Iy= Yм0Uy+ Bм0Iz+ Jм0 (7) Uz= Mм0Uy+ Zм0Iz+ Eм0 (8) где Iy, Uy, Iz, Uz – векторы токовых и потенциальных переменных y - полюсов и z - полюсов соответственно, Yм0 , Bм0 , Mм0 , Zм0 – матрицы линеаризованных неавтономных параметров компонента, Jм0, Eм0 – векторы линеаризованных автономных параметров многополюсного компонента Объединяя уравнения (7) и (8) совместно в одно матричное уравнение, получим
(9) Или, окончательно P = Wм0 Q + Sм0 (10) где
P = , Q = – векторы зависимых и независимых переменных многополюсного компонента,
Wм0 = , Sм0= –матрица и вектор автономных линеаризованных параметров многополюсного компонента. Объединяя компонентные уравнения всех многополюсников системы, получим объединенные матричные уравнения компонентов схемы. Пример  Скалярные уравнения многополюсника  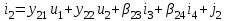 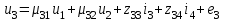  Матричное уравнение многополюсника
20 . Объединенное уравнение компонентов схемы Пусть имеется схема, содержащая m компонентов произвольного типа, уравнения которых имеют вид P1 = (Wм0)1Q1 + (Sм0)1 ……. Pk = (Wм0)kQk + (Sм0)k ……. Pm = (Wм0)m Qm + (Sм0)m Объединяя эти уравнения в одно матричное уравнение, получим P = Wм0 Q + Sм0 (11) где  , , 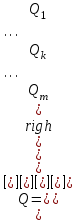 , , 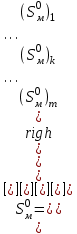
Wм0 = Объединенное уравнение совокупности всех многополюсных компонентов схемы (11) также имеет вид, совпадающий с уравнением (10), при этом матрица Wм0 будет иметь структуру диагональной блочной матрицы, в которой каждый блок описывает какой либо из компонентов схемы. Непременным условием для выбора вида компонентных уравнений является возможность представления их параметров в смешанной (гибридной) форме. Такая форма допускает использование как безразмерных, так и размерных параметров, при этом размерность параметров может быть различной для одного и того же компонента. Характер переменных в компонентных уравнениях зависит от физической природы объектов. В целях достаточной общности в настоящее время широко используется разделение переменных на две группы ‑ параллельных (продольных) и последовательных (поперечных) переменных. Помимо основных параллельных переменных  используются также интегральные параллельные переменные используются также интегральные параллельные переменные  Аналогично, помимо основных последовательных переменных Аналогично, помимо основных последовательных переменных 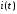 используются также интегральные последовательные переменные используются также интегральные последовательные переменные  В электротехнических системах основными параллельными переменными  являются полюсные напряжения, а основными последовательными переменными являются полюсные токи являются полюсные напряжения, а основными последовательными переменными являются полюсные токи  Интегральными параллельными переменными в электротехнических системах являются потокосцепления Интегральными параллельными переменными в электротехнических системах являются потокосцепления  , а интегральными последовательными переменными являются заряды , а интегральными последовательными переменными являются заряды  В табл.1 приводится перечень различных систем с указанием физического смысла используемых в них основных и интегральных переменных Таблица 1
30. Управляемые источники и эквивалентные схемы многополюсников В таблице приведены основные уравнения и эквивалентные схемы управляемых источников.
Запишем уравнение (5) для y - полюсов, выделив слагаемое при 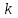 =i в первой сумме и опустив для простоты верхний индекс =i в первой сумме и опустив для простоты верхний индексii=yiiui+ 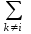 yikuk + yikuk +  βilil + ji (для y - полюсов) (12) βilil + ji (для y - полюсов) (12)Очевидно, что уравнение (12) описывает цепь, представляющую собой параллельное соединение проводимости yii, k управляемых источников типа JU и l управляемых источников типа JI. Аналогично, запишем уравнение (6) для z - полюсов, выделив слагаемое при  =j второй сумме и опустив для простоты верхний индекс =j второй сумме и опустив для простоты верхний индекс uj =zjjij+ 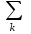 μikuk + μikuk +  zilil + ej (для z - полюсов) (13) Очевидно, что уравнение (13) описывает цепь, представляющую собой последовательное соединение сопротивления zjj, k управляемых источников типа EU и l управляемых источников типа EI. Таким образом, любой многополюсник может быть представлен эквивалентной схемой, содержащей некоторые двухполюсники и управляемые источники. zilil + ej (для z - полюсов) (13) Очевидно, что уравнение (13) описывает цепь, представляющую собой последовательное соединение сопротивления zjj, k управляемых источников типа EU и l управляемых источников типа EI. Таким образом, любой многополюсник может быть представлен эквивалентной схемой, содержащей некоторые двухполюсники и управляемые источники. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||