шпоры сопромат. 1. Метод перемещений. Определение усилий в системе, 1 раз кинемат неопределимой
 Скачать 1 Mb. Скачать 1 Mb.
|
|
21. Вынужденные колебания системы с одной степенью свободы. Имеет место при действии силы F(t) изменяющ. во времени по гармоническому закону. Определяется третьим слагаем 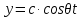 , где с – амплитуда вынужденных колебаний. , где с – амплитуда вынужденных колебаний.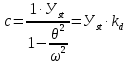 , где , где 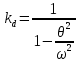 –динамический коэф при не учёте сил сопротивления; –динамический коэф при не учёте сил сопротивления; 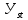 - статический прогиб. Последняя формула недостаточно точна в области резонанса при - статический прогиб. Последняя формула недостаточно точна в области резонанса при 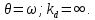 22. Собственные колебания системы с «n» степенями свободы. Вековое уравнение. Число возможных форм свободных колебаний равно числу степеней свободы упругой системы. Рассмотрим невесомую систему с n сосредоточенными массами.Получисли Система выведена из состояния равновесия каким-то воздействием, после его прекращения будет совершать свободные колебания. При движении масс возникнут силы инерции 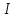 . Обозначим отклонения масс у1…уn; А1…Аn. Уравнение движения масс: . Обозначим отклонения масс у1…уn; А1…Аn. Уравнение движения масс: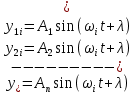 , где , где 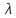 – начальная фаза колебаний – начальная фаза колебаний Сила инерции: 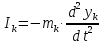 ; ;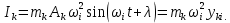 Перемещение точки k от всех инерционных сил: 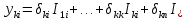 или с учетом значений сил инерции: или с учетом значений сил инерции: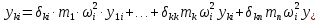 или или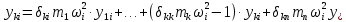 . .Это уравнение справедливо при любом значении k, поэтому запишем систему уравнений. 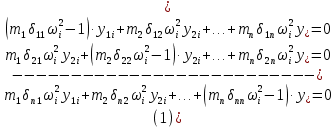 Получили систему уравнений, которая имеет не нулевое решение только в том случае, когда определитель часто, называют вековым уравнением, равен 0 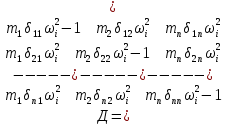 При раскрытии определителя получим полном n-ой степени относ. 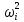 . Совокупность частот данной системы составляет спектр ее частот. Первая низкая частота называется частотой основного тона колебаний, следующая по порядку - первым обертоном. Для практических целей часто бывает найти min частоту – она предствляет наибольшую опасность, в смысле возможности возникновения резонанса с нейтральной нагрузкой. . Совокупность частот данной системы составляет спектр ее частот. Первая низкая частота называется частотой основного тона колебаний, следующая по порядку - первым обертоном. Для практических целей часто бывает найти min частоту – она предствляет наибольшую опасность, в смысле возможности возникновения резонанса с нейтральной нагрузкой. 23. Главные формы свободных колебаний Если направление перемещ. 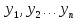 выбрать так, чтобы побочные перемещ. выбрать так, чтобы побочные перемещ. 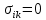 , то ур-ние частот распадается на отд. ур-ния, содержащие только главные координаты , то ур-ние частот распадается на отд. ур-ния, содержащие только главные координаты 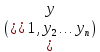 , а соотв. формы колебаний гл. формами колебаний. Они обособлены друг от друга и каждая из них происх. со своей определ. частотой , а соотв. формы колебаний гл. формами колебаний. Они обособлены друг от друга и каждая из них происх. со своей определ. частотой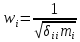 Рассм. это на примере: Рассм. это на примере:Пр. Определение частоты свободных колебаний Система им. 2 степени свободы. Детерминант: 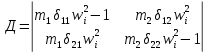 Для симметричных систем с симметр. располож. массами возможны симметричн. и антисимм. колебания Главные перемещ. вычисл. как групповые от парных един. сил (эпюры М1 и М2). 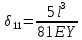 ; ; 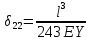 ; ; 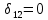 . .а) ур-ние частот для симметр. колебаний 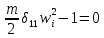 т.к. групповые перемещ. нах. от парных един. сил, то масса входит в вековое ур-ние с коэф-том 1/2: 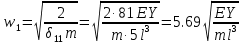 б) ур-ние частот для обратносимм. колебаний 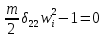 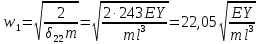 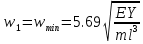 – частотаосновного типа колебаний – частотаосновного типа колебаний24. Приближенная оценка частоты осн. тона колебаний Во многих случаях определение всех частот свободных колебаний оказыв. излишним и достаточно отыскать только первую – низшую частоту. Для отыскания 1-й частоты м.б. применены разл. приближ. методы, не требующ. решения векового ур-ния. Исходя из св-в определителя частот проф. А.Ф.Смирновым были предложены пределы между кот. заключена частота осн. тона колебаний. 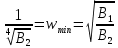 , где , где 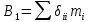 , ,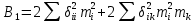 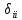 , ,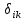 – гл. и побочн. перемещ. сист. от действия един. сил в точках прилож. сосредоточ. масс – гл. и побочн. перемещ. сист. от действия един. сил в точках прилож. сосредоточ. масс 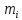 и и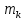 . .25. Вынужденные колебания системы с nстепенями свободы.Применение метода сил.Система уравнений для определения амплитудных значений сил инерции. 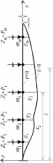 При движении на упругую систему вибрационной гармонической нагрузки ВСФ будут изменяться во времени, а их наибольшие значения(амплитуды) будут зависеть от частот возмущающих сил. Для системы с n степенями свободы возможны неск. случаев резонанса.В задачу динамического расчета входит определение амплитуды внутренних усилий,а также проверка системы на резонанс.Для этого применяют метод сил или метод перемещений.Рассмотрим метод сил. Рассмотрим упругую систему с точечными массами ,на которую действуют вибрационные силы. При движении на упругую систему вибрационной гармонической нагрузки ВСФ будут изменяться во времени, а их наибольшие значения(амплитуды) будут зависеть от частот возмущающих сил. Для системы с n степенями свободы возможны неск. случаев резонанса.В задачу динамического расчета входит определение амплитуды внутренних усилий,а также проверка системы на резонанс.Для этого применяют метод сил или метод перемещений.Рассмотрим метод сил. Рассмотрим упругую систему с точечными массами ,на которую действуют вибрационные силы. 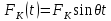 Перемещение любой массы мiв произвольный момент времени выражается:  (1) где Х1..Хn (1) где Х1..ХnАмплитуды сил инерции соответствующих масс.  -перемещения по направлению силы инерции Хi,вызванное единичными силами Хi… Хn -перемещения по направлению силы инерции Хi,вызванное единичными силами Хi… Хn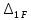 перемещение по направлению Хiот амплитудных значений вибрационных нагрузок. При гармонических вынужденных колебаниях с част. перемещение по направлению Хiот амплитудных значений вибрационных нагрузок. При гармонических вынужденных колебаниях с част.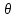 перемещение массы мiи её ускорение: перемещение массы мiи её ускорение: 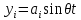 ( ( 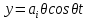 ) : ) : 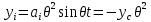 Сила инерции массы мi Сила инерции массы мi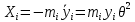 откуда откуда 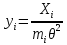 Подставив это выражение в уравнение(1) получим : Подставив это выражение в уравнение(1) получим :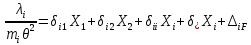 ; ;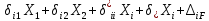 =0; =0;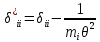 В результате получается сис-маур-й позволяющаяопр-тьнаи-шие (амплитудные значеня сил инерции) 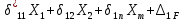 =0 =0 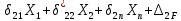 =0 =0 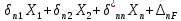 =0 Система уравнений по форме аналогична системе канонических ур-й метода сил. Однако,неизвестные являются не р-им, отборных связей\, а амплитуды сил инерции масс,которые могут возникнуть ,как в стат.опр-й,так и в стат.неопр.сист-х.При этом динамические изгиб.моменты: =0 Система уравнений по форме аналогична системе канонических ур-й метода сил. Однако,неизвестные являются не р-им, отборных связей\, а амплитуды сил инерции масс,которые могут возникнуть ,как в стат.опр-й,так и в стат.неопр.сист-х.При этом динамические изгиб.моменты: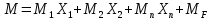 26.Перемещения и реакции от динамической нагрузки. Теорема о взаимности работ 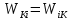 .Работа сил сост-я «К» на перемещение в состояние «i» равна раб. сил сост-я «i» на перемещ-е сост. «К». При этом динам-ие силы и перемещения считают изменяющимися по гармонич.зак. с одинак.частотой .Работа сил сост-я «К» на перемещение в состояние «i» равна раб. сил сост-я «i» на перемещ-е сост. «К». При этом динам-ие силы и перемещения считают изменяющимися по гармонич.зак. с одинак.частотой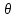 . Т.обз.перем: Взаимность перемещ.относ.к амплитудным перемещ-ям от одиночн.сил . Т.обз.перем: Взаимность перемещ.относ.к амплитудным перемещ-ям от одиночн.сил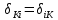 . Аналогично выраж-сявзаим-ть амплитуды динамич.р-й . Аналогично выраж-сявзаим-ть амплитуды динамич.р-й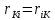 (т.Релея) и взаимность амплитуд динамич. перемещ. и р-ий (т.Релея) и взаимность амплитуд динамич. перемещ. и р-ий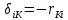 Приравнивая работу статич-й единичной силы сост-я «i» на перемещ в сост «к» вызв-ыхдинамич-й нагрузкой 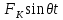 и и 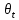 получ. форм. для ампл. динамич.перемещ. получ. форм. для ампл. динамич.перемещ. 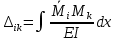 где где 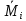 изиб. Момент от силы изиб. Момент от силы 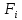 =1. =1. 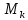 изгиб.момент от динамич.нагр.сучаст.сил инерции. изгиб.момент от динамич.нагр.сучаст.сил инерции.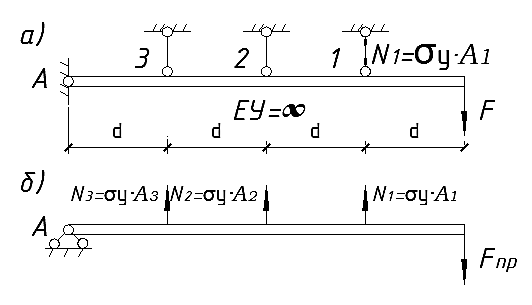 27.Расчет статически неопределимых рам по методу сил. 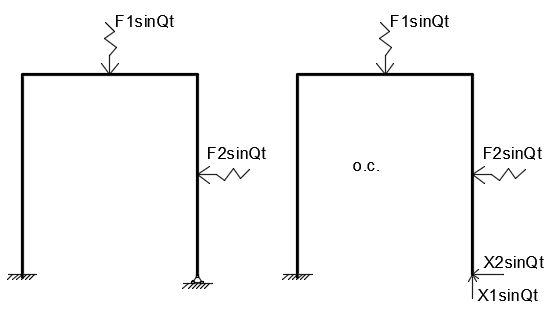 Рассм. раму, на которую действует вибрац. нагрузка одинаковой частоты. F(t)=FksinQt Рассм.установившиеся колебания. При этом реакции внутр.усилия и перем-я будут изм.по з-ну sinQt. Любые неизвестные в о.с. Xk(t)=XksinQt. Здесь Xk-амплитудное зн-е неизв.реакции связи. Усл.равенства нулю полных динам.перем-й по напр-ям отброшенных связей. 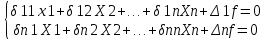 Здесь δkm-амплитудное зн-е перемещ.по напр-ю силы Xk от ед.силы Xm=1*sinQt. Δkf-амлитудные перемещ.от нагрузки по напр-ю той же силы. Эти вел-ны опр.по ф-ле 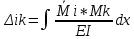 При этом возн.трудности, связ.с опр.-ем изгиб.мом-ов от динам.нагрузки с учетом инерционных сил. Поэтому метод сил оказ.малоэффект.для динам.расчёта рам. 28. Динамический расчет статически неопределимых рам по методу перемещений 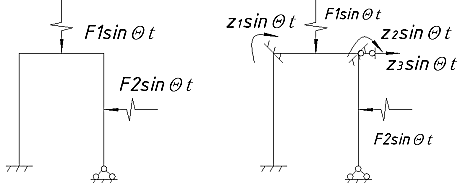 Zi(t) – динамические неизвестные перемещения Канонические ур-ния по направлению «k»-той связи: 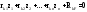 rim – амплитудные значенияреакций введенных связей от единичных вибрационных перемещений КiF – амплитудные значенияреакции введенной связи от вибрац. нагрузки Эти реакции отличаются от соответствующих величин, используемых в статических расчетах – в них учтены силы инерции сосредоточенных или равномерно распределенных масс стержней рамы с помощью поправочных функций к формулам для статических реакций. 29. Понятие о расчете в упругой стадии и по методу предельного равновесия Р 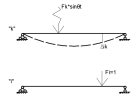 ассмотренные раннее методы расчета конструкций позволяют установить картину распределения внутренних усилий в упругой стадии работы. При этом «методы упругого расчета» не дают ответа на вопрос об истинном запасе прочности сооружений. Исчерпание несущей способности конструкций происходит за пределами упругой стадии работы. ассмотренные раннее методы расчета конструкций позволяют установить картину распределения внутренних усилий в упругой стадии работы. При этом «методы упругого расчета» не дают ответа на вопрос об истинном запасе прочности сооружений. Исчерпание несущей способности конструкций происходит за пределами упругой стадии работы. ОА - упругая стадия деформирования, где 1.  , , 2.  , , - расчет по допускаемым напряжениям - расчет по допускаемым напряжениям АВ – пластическая стадия деформации, где 3.  (для данного материала) (для данного материала)  ВС – стадия упрочнения Для проведения практических расчетов реальную диаграмму удобно заменить упрощенной диаграммой Прандля, отвечающей идеальному упруго-пластическому мат-лу. Идея метода предельного равновесия сост. в том, что конструкция рассматривается в момент непосредственно предшествующий ее разрушению. При этом ещё выполняются усл. равновесия для внутренних и внешних сил, достигающих предельного значения. М  етод позволяет исключить из рассмотрений Iстадию работы конструкций и найти предельную нагрузку из анализа IIстадии работы. етод позволяет исключить из рассмотрений Iстадию работы конструкций и найти предельную нагрузку из анализа IIстадии работы.  30. Предельное равновесие системы с растянутыми элементами Стержни системы (а) изготовлены из мат-ла с диаграммы Прандля. При достижении в наиб.напряженном стержне  ещё не происходит исчерпания несущ. способности системы. При этом ещё не происходит исчерпания несущ. способности системы. При этом  и возможно дальнейшее увеличение нагрузки, при кот.усилия N2 и N3 будут возрастать при и возможно дальнейшее увеличение нагрузки, при кот.усилия N2 и N3 будут возрастать при  . .При появлении текучести в стержне 2 несущая способность системы также ещё не исчерпана. Когда 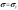 во всех 3х стержнях, то дальнейшее возрастание нагрузки не возможно. во всех 3х стержнях, то дальнейшее возрастание нагрузки не возможно. Соответствующая предельная нагрузка Fпр для системы 2жды статически неопределимой находится из ур-ния равновесия для предельного состояния (б) 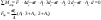 31. Предельное равновесие изгибаемой балки. 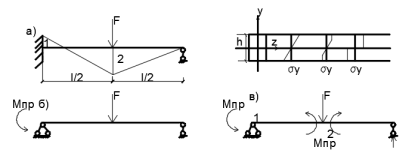 R=Fпр/2-Мпр/l (сумма М1=0) R=Fпр/2-Мпр/l (сумма М1=0)При появл.текучести в кр.волокнах наиб.напряженные сечения 1(рис.а) ещё не исчерпыв.нес.сп-сть балки. При дальнейшем увел-ии нагр.текучесть проник.вглубь сеч-я вплоть до появл.в нём пласт.шарнира. М1=Мпр=σy*Wпл Согл.последней эпюре Wпл=2Sz; Wпл=h^2b/4 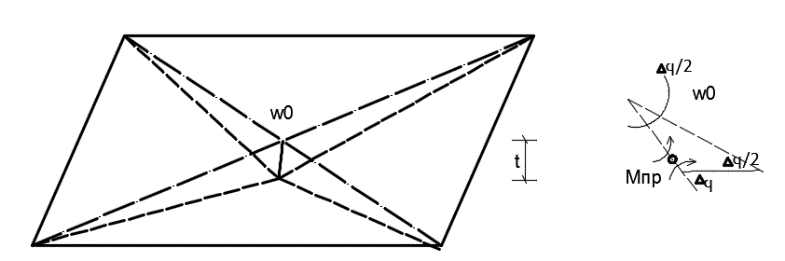 Нес.сп-сть балки не исчерпыв.Система превращ.в ст-ки опред.и геом.неизменяемую(рис.б). Нес.сп-сть балки не исчерпыв.Система превращ.в ст-ки опред.и геом.неизменяемую(рис.б).Когда в сеч.2 М=Мпр система превращ.в мех-м (рис.в). Из равновесия мех-ов в пред-ом сост. М2=Мпр=R*l/2=(Fпр/2-Мпр/2)l/2=Fпр*l/4-Мпр/2 Fпр=1,5Mn*n/lM2=6Мпр/l  Для анализа пред.равнов.сложн.сист.исп.стат-ки и кинем.теоремы в пред-м равновесии и вытек.из них св-ва пред.нагрузок. Для анализа пред.равнов.сложн.сист.исп.стат-ки и кинем.теоремы в пред-м равновесии и вытек.из них св-ва пред.нагрузок.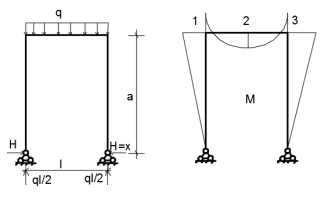 32. Теоремы о предельном равновесии 32. Теоремы о предельном равновесииСтатическая теорема: в произвольном случае упруго-пластич. тела нагрузка, соответств. статич. возможному состоянию, меньше, чем предельная. В упругой стадии значение H=х определяется, например методом сил. После перехода системы в упруго-пластич. стадию эти значения изменяются. Для выяснения возможных пределов изменения «q» и «х» запишем условия-ограничения: считаем, что переход в сост. предельного равновесия происходит в следствии достижения моментами соответств. предельного значения Mпр Ограничения: Уз.1: 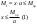 Уз.2: 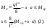 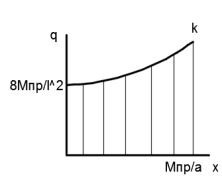 Неравенствам (1) и (2) соответствует область статически возможных значений «q» и «х»: Неравенствам (1) и (2) соответствует область статически возможных значений «q» и «х»:В соответствии со статич. теоремой предельное знач. нагрузки «q» будет  точка «k» диаграммы. точка «k» диаграммы.Анализируя равновесие ригеля рамы в предельном сост. получим аналогичное знач. qпр  Кинематическая теорема: нагрузка, соответствующая кинематич. возможному состоянию, больше, чем предельная. Сравниваются величины нагрузок, соответствующих различным кинемат. возможн. сост. системы и выбираются наименьшие. Для любой кинематич. возможной схемы перемещение рамы имеет ур-ие равновесия:  33. Предельное равновесие прямоугольной пластины Рассмотрим свободно опертую пластину, загруженную по всей площади равномерно распределенной нагрузкой интенсивностью р. При каком-то параметре нагрузки в центре пластины  Текучесть будет постепенно проникать к нейтральному слою пластины и распространяться по ее толщине. В пределе образуются пластические шарниры по диагоналям пластины и она начнет перемещаться по вертикали как механизм без дальнейшего увеличения нагрузки. Приближенный метод определения предельной нагрузки основан на энергетическом методе. Для квадратной пластины со стороной а работа внешних сил 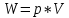 Где V – объем пирамиды с высотой, равной прогибу пластины 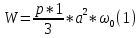 Предельный пластический момент в полоске с шириной равной 1: 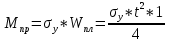 Углы взаимного поворота треугольных частей пластины во всех трех точках пластины равны: 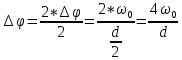 d – длина диагонали Работа изгибающих моментов на единице длины диагоналей равна 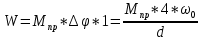 А на длине двух диагоналей: 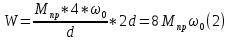 Приравнивая (1) и (2) получим: 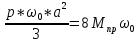 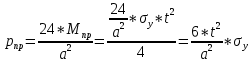 |
