шпоры сопромат. 1. Метод перемещений. Определение усилий в системе, 1 раз кинемат неопределимой
 Скачать 1 Mb. Скачать 1 Mb.
|
|
1.Метод перемещений. Определение усилий в системе, 1 раз кинемат. неопределимой. При расчете статически неопред. систем по методу сил за лишние неизвестные принимают- ся усилия в лишних связях, после определения которых, находят усилия внутренние, а потом уже перемещения. Можно решить задачу иначе: найти перемещения, а потом установить соответств. им распределения усилий. В методе перемещений за основные неизвестные принимаются перемещения фиксированных сечений или узлов системы. Число и вид неиз- вестных перемещений принимают за основные, называют степенью кинематич. неопредел. Абсолютно жесткий брус АВ поддерживается 3-мя стержнями. (рис.1) 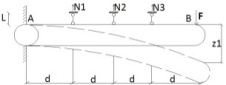 Рис.1 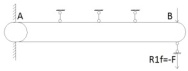 Рис.2 Рис.2Система 2-ды статически неоп-ма. В то же время, удлинения, а, следовательно, и усилия всех Стержней определяются одним вертикальным перемещением Z, степень кинематичнеопре- делимости=1. Устраним перемещение Z, введя по его направлению связь. (рис.2) Сообщим этой связи принудительное смещение Z, которое найдем из условия, что суммар- ная реакция R1в этой связи должна обратиться в 0, т к в действительности связь отсутствует. 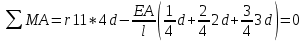 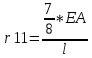 -реакция от смещения z1=1 -реакция от смещения z1=1R 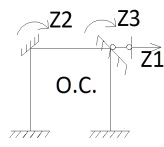 1z=r11*z1. Согласно принципу суперпозиции 1z=r11*z1. Согласно принципу суперпозицииУсловие отсутствия полной реакции присоединенной связи получит вид: R1=R1z+R1f=r11z1+R1f=0 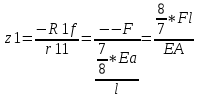 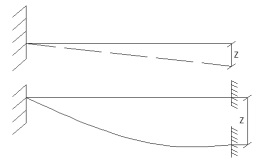 Искомое значение усилий: 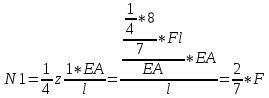 ;N2=4/7*F; N3=6/7*F ;N2=4/7*F; N3=6/7*F2.Степень кинематической неопределимости системы. Зависит от свойств модели, с помощью которой схематизируется работа деформ. системы. Различают 2 типа моделей стержневых конструкций: с растяжимыми сжимаемыми(EA≠∞) и нерастяжимыми стержнями (EA=∞). Первая модель представляет 3 характерных вида сое- динения стержней в узле: а 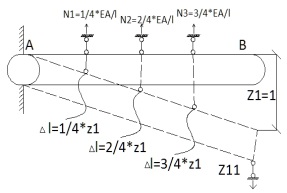 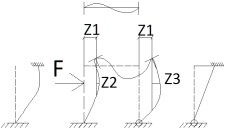 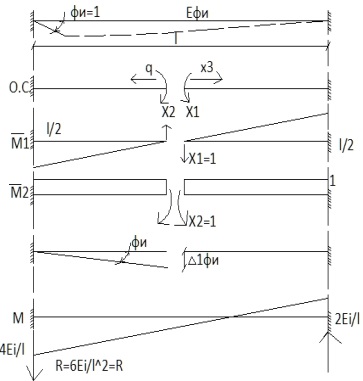 ) )  б б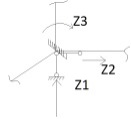 ) )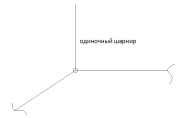 в) в) 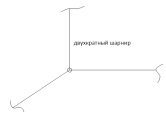 Вторая модель. В действительности все стержни имеют конечную жесткость на растяжение-Сжатие, однако, в ряде случаев значения указанных деформаций малы по сравнению с деформациями изгиба и ими пренебрегают, что соответствует 2 модели.Раму будем рассматривать как ансамбль отдельных стержневых элементов, объемных в узлах. В целом, деф.состояние рамы будет определено 3 мя перемещениями узлов: Z1-линейное перемещение; Z2,Z3 –углы поворота узлов. Степень статической неопред. n=ny+nл, где ny,nл-количество угловых и линейных перемещений узлов сис.Представим основную систему с присоединенными связями, устраним эти перемещения. Условные защемления введенные в узлы и устраняющие углы поворота называютплавающими заделками. Уравнение равновесия рамы, выраженное через перемещения Z1,Z2,Z3,получим прировняв к 0 суммарные реакции в присоединенных связях. Сосредоточенную силу в линейной связи и моменты в угловыхсвязях Вторая модель. В действительности все стержни имеют конечную жесткость на растяжение-Сжатие, однако, в ряде случаев значения указанных деформаций малы по сравнению с деформациями изгиба и ими пренебрегают, что соответствует 2 модели.Раму будем рассматривать как ансамбль отдельных стержневых элементов, объемных в узлах. В целом, деф.состояние рамы будет определено 3 мя перемещениями узлов: Z1-линейное перемещение; Z2,Z3 –углы поворота узлов. Степень статической неопред. n=ny+nл, где ny,nл-количество угловых и линейных перемещений узлов сис.Представим основную систему с присоединенными связями, устраним эти перемещения. Условные защемления введенные в узлы и устраняющие углы поворота называютплавающими заделками. Уравнение равновесия рамы, выраженное через перемещения Z1,Z2,Z3,получим прировняв к 0 суммарные реакции в присоединенных связях. Сосредоточенную силу в линейной связи и моменты в угловыхсвязях3.Значение реакций и внутренних усилий в стержне, как элементе основной системы метода перемещений. Методом сил построим эпюру моментов М, приход.на единицу перемещения от поворота заделки на угол ϕ=1. d11x1+d12x2+d13x3+ᴧ1ϕ=0 d21x1+d22x2+d23x3+ᴧ2ϕ=0 d31x1+d32x2+d33x3+ᴧ3ϕ=0 x3=0;d13….=0;d12=0 d  11x1+ᴧ1ϕ=0 11x1+ᴧ1ϕ=0d22x2+ᴧ2ϕ=0 d11=…l^3/12EI d22=…l/EI ᴧ1ϕ=-1/2*ϕ ᴧ 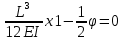 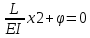 При ϕ=1 х1=6EI/l^2 x2=-EI/l M=M1x+M2x2 Полученные результаты расчета балок приведены в таблицах. 4. Каноническая форма записи уравнений метода перемещений. 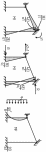 Если в точках системы компоненты, перемещения которых неизвестны, не приложены соответствующего рода силы, то неизвестные перемещения Zк определяются из уравнений записанных на основе теоремы Лагранжа Если в точках системы компоненты, перемещения которых неизвестны, не приложены соответствующего рода силы, то неизвестные перемещения Zк определяются из уравнений записанных на основе теоремы Лагранжа 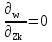 . .Эти уравнения нелинейные кроме случаев, когда физический закон линейный, они являются одновременно условием экстремума функции. Точто этот экстремум есть минимум вытекает из очевидного факта: 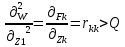 , , Поскольку это есть единственная реакция в точке К, то направление перемещения 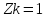 . .Рассмотрим например линейно-упругую рамную систему, имеющую 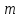 стержней и стержней и 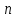 неизвестных перемещений неизвестных перемещений 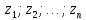 . .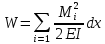 , где , где 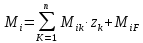 – момент в стержне – момент в стержне 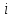 от перемещения от перемещения 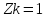 и и 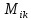 - момент в стержне - момент в стержне 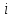 от внешней нагрузки. от внешней нагрузки.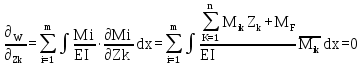 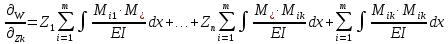 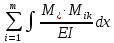 - величина численно равная работе внутренних сил, равна в то же время работе внешних сил состояния n на перемещение к состоянию k, - величина численно равная работе внутренних сил, равна в то же время работе внешних сил состояния n на перемещение к состоянию k,где 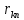 – реакция введенной связи от – реакция введенной связи от 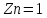 , на введенную связь , на введенную связь 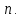 В итоге получается: 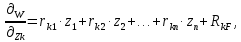 где где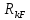 - реакция введенной связи - реакция введенной связи 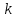 от внешнего воздействия от внешнего воздействия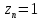 . .Учитывая что 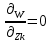 и придавая значения 1,2,…, и придавая значения 1,2,…,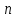 получили: получили: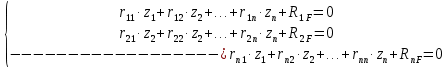 - Она называется системой канонических уравнений метода перемещений. Каждое уравнение выражает ту мысль, что общая реакция введенной связи равна нулю. В матричной форме: 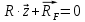 , где , где 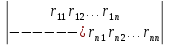 - матрица жесткости. - матрица жесткости.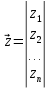 – вектор перемещений. – вектор перемещений.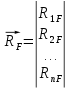 – вектор реакций введенных связей. – вектор реакций введенных связей.5. Определение коэффициентов и свободных членов канонических уравнений метода перемещений статическим способом(на примере рамы) 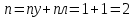 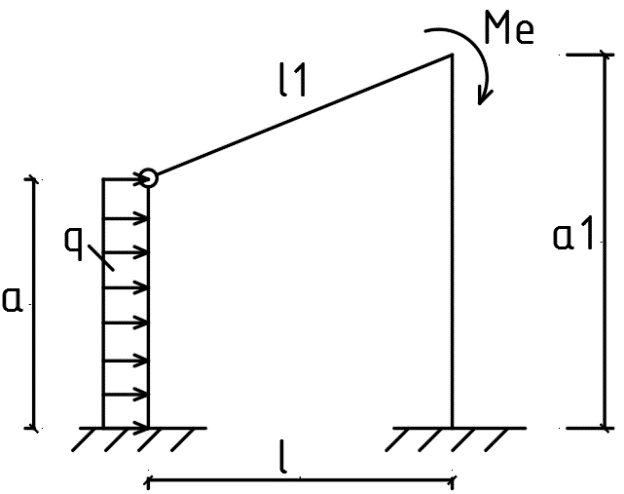 Без учета продольных деформаций стержней рама имеет 2 неизвестных перемещения: 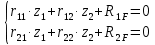 Построим эпюры изгибающих моментов от кинематических воздействий и изгибающих моментов: 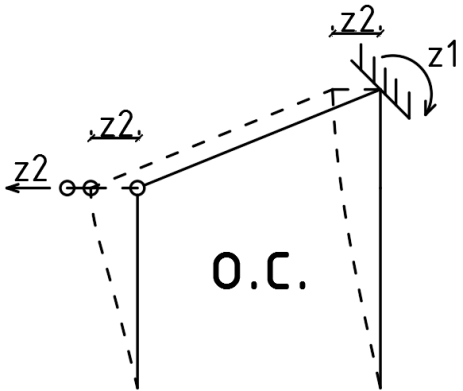 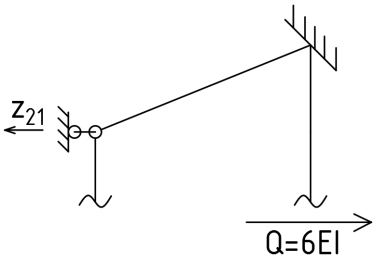 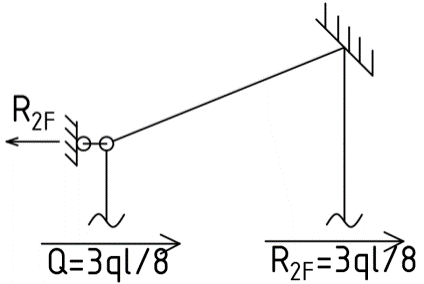 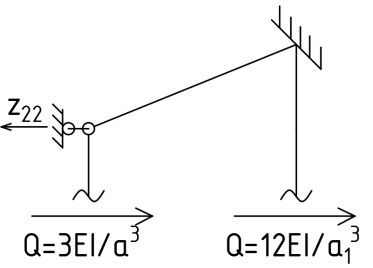 6. Общий способ определение коэффициентов и свободных членов канонических уравнений метода перемещений. Позволяет путем перемножения соответствующих эпюр получить формулы для реакций в общем виде. Коэффициенты уравнений( 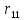 и т.д.) представляющие собой единичные реакции определяются по формуле: и т.д.) представляющие собой единичные реакции определяются по формуле: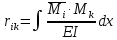 Д На основании теоремы о взаимности работ имеем 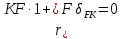 , где , где 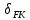 - перемещение статически неопределимой системы в состоянии - перемещение статически неопределимой системы в состоянии 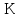 по на направлению нагрузки по на направлению нагрузки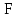 . .При 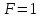 зависимость по существу представляет взаимосвязь реакциий и перемещений(2-я т.Релея) зависимость по существу представляет взаимосвязь реакциий и перемещений(2-я т.Релея)Для определения 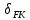 возьмем в качестве единичного состояния статически определимую балку-консоль и приложим к ней силу возьмем в качестве единичного состояния статически определимую балку-консоль и приложим к ней силу 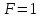 по направлению искомого перемещения. по направлению искомого перемещения.ля определения свободных членов представляющих собой реакции от внешней нагрузки рассмотрим состояние системы 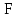 при действии внешней нагрузки и действие при действии внешней нагрузки и действие 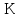 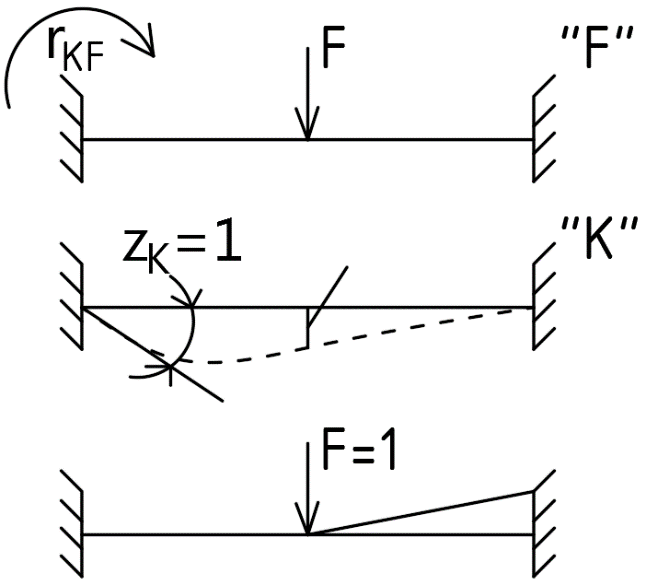 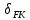 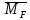 Эпюру моментов в ней обозначим 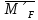 , тогда: , тогда: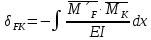 , где , где 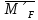 , - эпюра изгибающих моментов от нагрузки , - эпюра изгибающих моментов от нагрузки 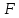 в статически определимой системе полученной и заданной устранением лишних связей в том числе обязательно той связи, реакция которой определяется. в статически определимой системе полученной и заданной устранением лишних связей в том числе обязательно той связи, реакция которой определяется.Рассмотренная выше рама дважды статически неопределима. 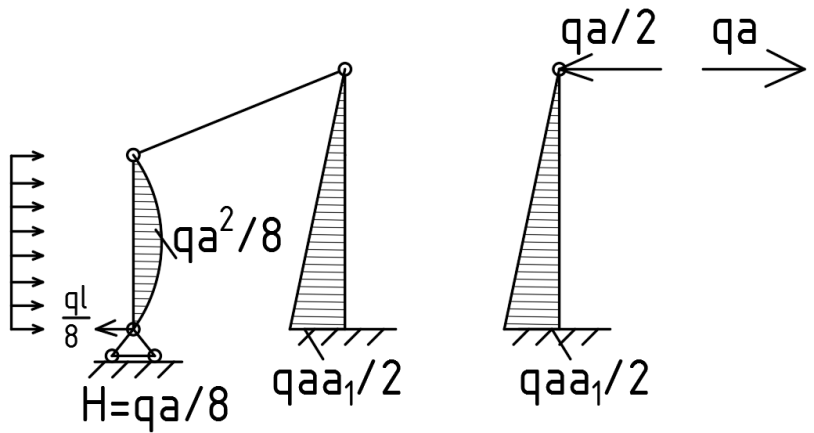 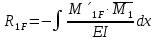 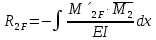 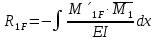 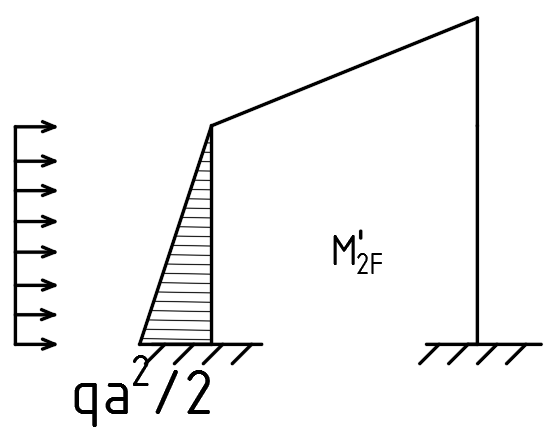 7. Особенности расчёта рам по методу перемещений с наклонными элемантами При использовании допущения об абсолютной жёсткости стержня на растяжение сжатие(2 модель ЕА≠∞), получаем уменьшение числа независимых линейных перемещений узлов системы , однако определение реакций в линейных связях при наличии наклонных стержней в этом случае, как правило усложняется. 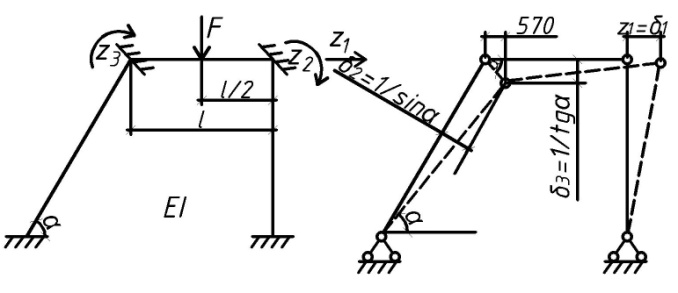 Во все узлы рамы, включая опорные ввели шарниры и получили величины относительных смещений на рисунке. Считаем, что повороте стежня его точки перемещаются по нормалям первоначальному положению оси стержня Эпюра моментов определяется относительным смещением концов стержней. 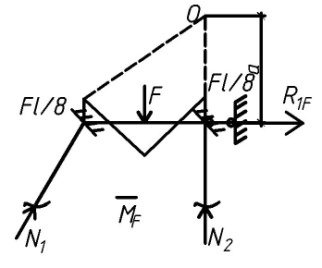 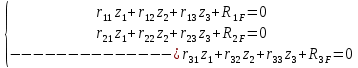 Коэффициенты нижнего блока уравнений, представленные моменты в угловых связях вычисляются обычным способом 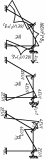 Из-за наклона стержней в сумму проекций войдёт продольная сила, что потребует её предварительного определения. Из-за наклона стержней в сумму проекций войдёт продольная сила, что потребует её предварительного определения.Обычно стараются составить уравнение равновесия так, чтобы в них не входили продольные силы, например реакция R1F 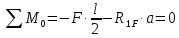 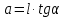 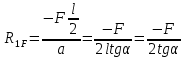 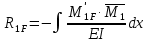 Где М’1F –эпюра изгибающих моментов в о.с. метода сил Реакции r11, r12, r13 могут быть найдены аналогично 8. Смешанный метод. Основная система. Канонические уравнения и определение их коэффициентов. Вводные замечания:  В методе сил за основное неизвестное принимались усилия xi-ые в методе перемещения независимые перемещения узлов системы zj. В методе сил за основное неизвестное принимались усилия xi-ые в методе перемещения независимые перемещения узлов системы zj.Лишние неизвестные xi, находятся из уравнений совместности деформаций. Перемещения zj определяются из уравнений равновесия. В смешанном методе за основные неизвестные принимаются частично усилия xi и частично перемещения zj Канонические уравнения Метод сил: n=7; метод перемещений n=7 Основная система образуется одновременно как освобождением, так и введением связей в заданную систему. Уравнения составляются из условий 2-ух типов: а) неразрывности перемещений по направлению лишних неизвестных в точках, где освобождены связи ∆1=0. б) Равенство нулю реакций в введённых закреплениях R2=0 R3=0. Для приведённых систем канонические уравнения имеют вид: 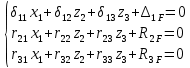 В матричной форме эти уравнения: 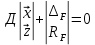 Где матрица Д матрица податливости жёсткости имеет следующую структуру: 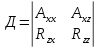 Верхние блоки состоят из перемещений ∆ik по направлению неизвестных xi. Определяются от неизвестных xi (блок Ахх) или неизв. zj (блок Axz). Аналогично блоки Rzx и Rzz состоят из реакций дополнительных связей от сил xi и перемещений zj. На основании теоремы о взаимности реакций и перемещений, т.е. элементы блока Axz и Rzx и будут представлять взаимнотранспонированные матрицы (Axz=-Aтzx) По этой причине матрица Д смешанного метода в целом несимметрична. Элементы блоков (Axx и Rzz) определяются так же как в м.с. и в м.п. соответственно. Элементы r21 и r31 блока Rzx определяются как в методе перемещений из равновесия узлов 2 и 3. r21=(a1+a2) 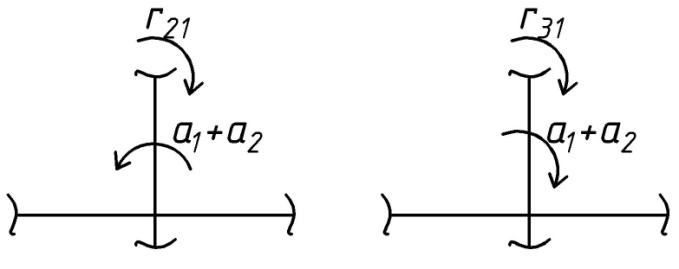 r31=-(a1+a2) Тогда 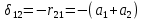 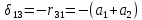 Свободные члены 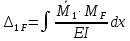 (метод сил) (метод сил)R2F и R3F определяются как в методе перемещений. Изгибающие моменты вычисляются по формуле: 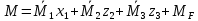 |
