шпоры сопромат. 1. Метод перемещений. Определение усилий в системе, 1 раз кинемат неопределимой
 Скачать 1 Mb. Скачать 1 Mb.
|
|
9. Комбинированное решение задач методами сил и перемещений. В ряде случаев для ускорения расчёта симметричных систем удобно расчленить все внешние воздействия на симметричную и антисимметричную составляющую. 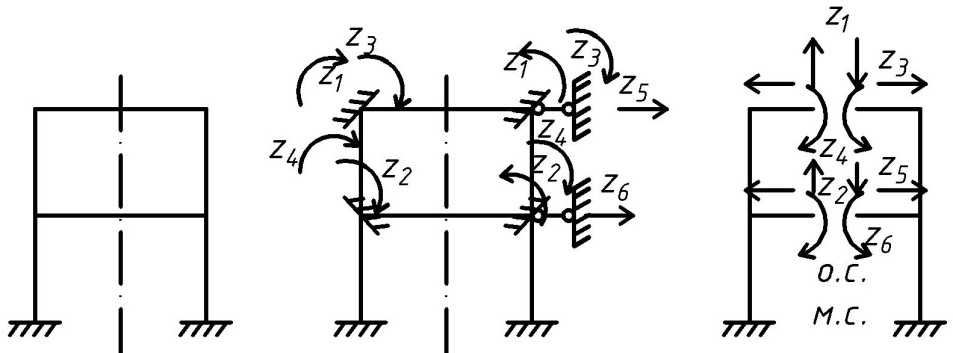 Распределение числа неизвестных для данной системы в зависимости от метода расчёта сведём в таблицу
На симметричную нагрузку расчёт следует проводить по методу перемещений. На антисимметричную нагрузку по методу сил. В каждом случае будет по 2 неизвестных.  Указанный подход называется комбинированным приёмом расчёта. Указанный подход называется комбинированным приёмом расчёта.Покажем распределение нагрузки на симметричную и антисимметричную составляющую результаты расчёта на 2 вида нагрузок по составляющим методам(м.п. и м.с.) необходимо сложить. 10. Основы устойчивости упругих систем С 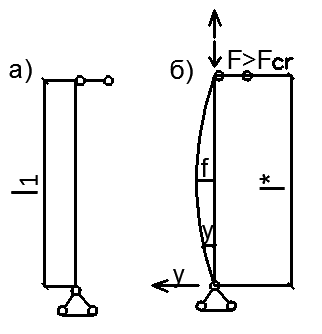 истемы, применяемые в кач-ве строительных конструкций под действием нагрузки должны находиться в состоянии устойчивого равновесия. истемы, применяемые в кач-ве строительных конструкций под действием нагрузки должны находиться в состоянии устойчивого равновесия.Устойчивостьюназыв. св-во сооружения сохранять своё первоначальное положение и соответствующую нагрузке первоначальную форму равновесия в деформированном состоянии. Особое внимание следует обращать на эл-ты работающие на сжатие т.к. при определенных значениях сжимающих сил может произойти потеря устойчивости стержня. Разрушение вследствие этого происходит мгновенно. 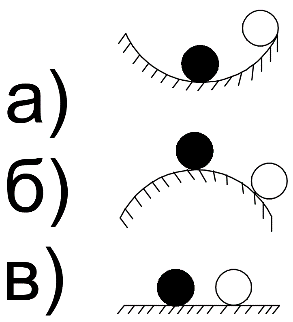 В смысле кач-ва равновесия различают: В смысле кач-ва равновесия различают: а) устойчивое б)неустойчивое в)безразличное Безразличное состояние равновесия есть как бы предел устойчивого и начало неустойчивого равновесия, поэтому оно считается критическим для системы. Потеря устойчивости– переход сооружения из устойчивого сост. в неустойчивое, соответствующая нагрузка назыв. критическая. Число возможных форм неустойчивого равновесия определяется степенью свободы системы. Степень свободы – число независимых геометрич. параметров, необходимых для определения положения точек системы потерявших устойчивость. 1 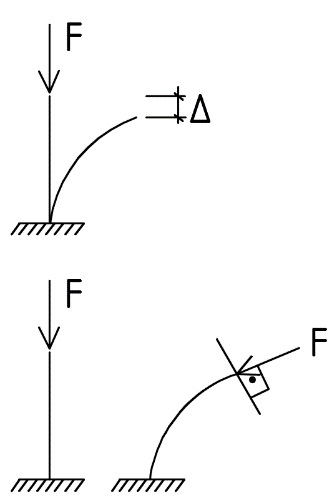 1. Основные критерии и методы исследования устойчивости упругих систем 1. Основные критерии и методы исследования устойчивости упругих системДействующие силы подраздел. на консервативные и неконсервативные. Работа определяется начальным и конечным положением точек системы. Силы, не отвечающие этому условию относ. к неконсервативным. Примером является следящая сила, ориентация которой меняется в пространстве. В строительстве преобладают консервативные системы для исследования которых применяют 3 осн-х метода: статический, энергетический, динамический. О 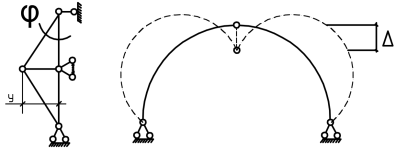 степенях свободы: 1 степень свободы. Потеря устойчивости со сменой формы деформированного состояния называется потерей устойчивости 1 рода. Потеря устойчивости 2 рода назыв. рост деформаций при отсутствии приращения. Связан с потерей несущей способности 3-шарнирной рамы. степенях свободы: 1 степень свободы. Потеря устойчивости со сменой формы деформированного состояния называется потерей устойчивости 1 рода. Потеря устойчивости 2 рода назыв. рост деформаций при отсутствии приращения. Связан с потерей несущей способности 3-шарнирной рамы. 12. Устойчивость систем с 1 степенью свободы Абсолютно жесткий (EI= 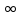 ) консольный стержень связан в основании упруго податливо относительно поворота. ) консольный стержень связан в основании упруго податливо относительно поворота.Ж  есткость связи k(величина момента, возникающего в основании при повороте опорного сечения на 1). Найдем статическим методом величину критической силы. При отклонении стержня на угол ϕ в основании возникает момент есткость связи k(величина момента, возникающего в основании при повороте опорного сечения на 1). Найдем статическим методом величину критической силы. При отклонении стержня на угол ϕ в основании возникает момент 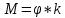 . Рассмотрим стержень в отклоненном состоянии (Рис. Б). Составим условие равновесия момента . Рассмотрим стержень в отклоненном состоянии (Рис. Б). Составим условие равновесия момента 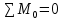 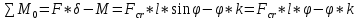 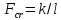 13. Устойчивость стержня на двух шарнирных опорах. Определение критической силы. Рассмотрим стержень сжимаемый силой F. При 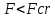 прямолинейная форма равновесия стержня устойчива (осевое сжатие). прямолинейная форма равновесия стержня устойчива (осевое сжатие).При 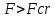 она устойчива и стержень выпучивается, т.е. будет испытывать продольный изгиб. она устойчива и стержень выпучивается, т.е. будет испытывать продольный изгиб.При действии силы F стержень укорачивается и его длина 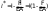 , где l- первоначальная длина стержня. , где l- первоначальная длина стержня.Рассмотрим случай, когда 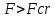 . Задача об определении критических сил сводится к решению приближенного уравнения изгиба: . Задача об определении критических сил сводится к решению приближенного уравнения изгиба: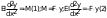 После подстановки (2) в (1) получим уравнение равновесия упругой системы в возмущенном состоянии: 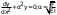 Для постоянного поперечного сечения непосредственным интегрированием диф. уравнения упругой линии решение находится в виде: 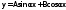 Произвольные постоянные определим из граничных условий задачи. При 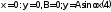 При 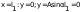 а) если А=0, то согласно последнего выражения не будет изгиба и стержень останется прямым б) 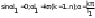 Тогда уравнение упругой линии (4) примет вид 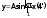 Здесь k определяет число полуволн синусоиды, теоретически возможных при продольном изгибе. Наименьшая сила способная создать продольный изгиб будет при k=1 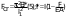 Выпучивание происходит по одной полуволне синусоиды. Установим связь между длинной прямого стержня в критическом состоянии l* и l1 При уменьшении F - l1 увеличивается (ф-ла 5) и стержень должен выпрямляться. В пределе l1 будет стремиться к l*, а сила F к Fcr.  Величиной по сравнению с единицей пренебрегают, тогда 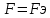 , т.е. при , т.е. при 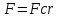 продольного изгиба еще нет. продольного изгиба еще нет.14. Устойчивость стоек плавно-переменного сечения. Определение критической силы. Диф уравнения равновесия стойки в отклоненном состоянии после потери устойчивости 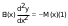 Моменты инерции стойки изменяются по закону 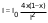 Тогда уравнение (1) будет 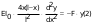 Это уравнение будет удовлетворять, если 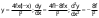 П 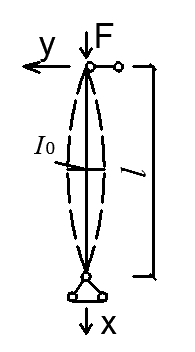 одставив в (2) получим одставив в (2) получим 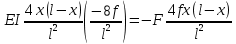 Откуда 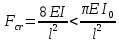 Значение критической силы 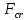 для любого стержня при любых его закреплениях можно представить: для любого стержня при любых его закреплениях можно представить: 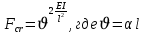 По формуле Эйлера 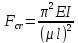 Прировняв правые части в двух последних выражениях, получим коэффициент приведения длины: 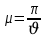 15. Расчет стоек переменного сечения на устойчивость методом конечных разностей. МКР является универсальным приближенным методом решения диф. уравнения. Кривую непрерывного изменения аргумента, например, 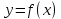 заменяют конечным (дискретным) множеством точек (узлов) и вместо функций непрерывного аргумента рассматривают функции дискретного аргумента. заменяют конечным (дискретным) множеством точек (узлов) и вместо функций непрерывного аргумента рассматривают функции дискретного аргумента.Производные, входящие в диф. уравнения заменяют соответствующими разностными отношениями. При этом диф уравнения заменяются системой алгебраической (разностной), а начальные и краевые условия разностными начальными и краевыми условиями для узловой функции. 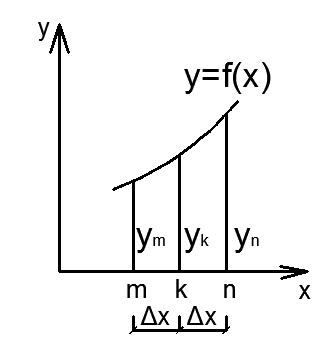 Вторая производная в точке k запишется 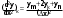 Для граничных узлов в уравнения будут входить за контурные точки, которые определяются в зависимости от вида закрепления. 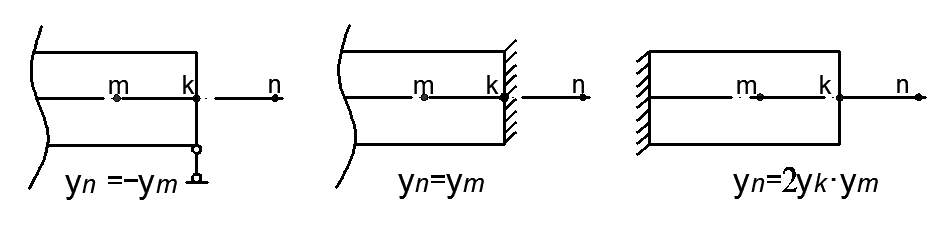  16. Устойчивость плоских рам. Составление характеристического уравнения. Д 1) рассм-тся только узловая нагрузка, не вызывающая поперечн. изгиба в стержне рамы 2) стержни считаются нерастяжимыми и несжимаемыми 3) при работе учитыв. нормальн. силы, возник. до потери устойч-и Рассм. раму. Пока 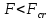 - равновесие устойчивое, единств. формой равновесия будет прямолинейн. - равновесие устойчивое, единств. формой равновесия будет прямолинейн.Существует такое знач. критич. параметра нагрузки Fcrпри котором кроме прямолин. полож. возможно еще другое изогнутое равновесное состояние. Расчет м.б. произведен любым из методов: методом сил или перемещений. Т.к. узловая нагрузка не вызывает моментов в осн.сист. ( 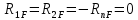 ), то кононич. ур-ния будут однородные ), то кононич. ур-ния будут однородные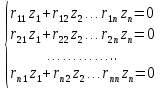 При потере уст-сти 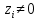 ,что возможно только тогда, когда определитель из коэф-тов ,что возможно только тогда, когда определитель из коэф-тов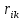 равен 0. равен 0.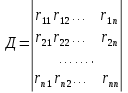 =0, из получ. характеристич. ур-ния находят критич. силу =0, из получ. характеристич. ур-ния находят критич. силу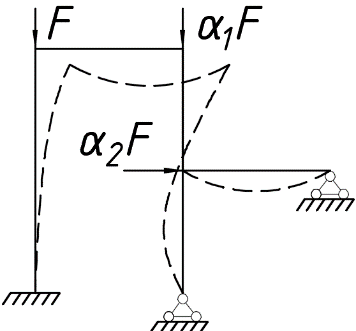 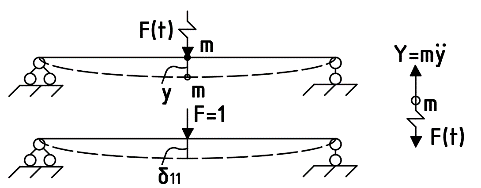 17. Динамические нагрузки и их особенности. Силы инерции. Динамика сооружений занимается разработкой принципов и методов расчета сооружений на действие динамических нагрузок. При этом возникают и играют существенную роль силы инерции масс этих нагрузок и самого сооружения. Динамические нагрузки делятся на следующие основные виды: 1. Вибрационная – создаваемая стационарными машинами и механизмами с движущимися частями. (например, электродвигатели, генераторами и тд) 2. Импульсивная – создаваемая падающими грузами и падающими частями силовых установок (напр., молотов, копров и тд) 3. Подвижная – положения которой в пролетах в сооружениях изменяется во времени. (напр., нагрузка от автомобилей, кранов и тд) К динамическим нагрузкам относятся ветровая, от взрывной волны, сейсмическая. Все динамические нагрузки вызывают колебания конструкций, на которые они действуют. 18. Основные методы решения задач динамики сооружений Динамический расчет производится для проверки сооружений на прочность, а также для определения величин динамических перемещений, скоростей и ускорений, которые не должны превосходить допускаемых пределов. Для решения задач динамических сооружений применяется 2 основных метода: 1. Статический – основанный на применении уравнений динамического равновесия, которые отличаются от уравнений статического равновесия дополнительным учетом сил инерции согласно принципам Даламбера. Инерционные силы по направлению осей x, y, z: 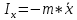 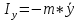 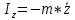 2. Энергетический – основанный на применении закона сохранения энергии Ломоносова, согласно которому сумма кинетической и потенциальной энергии упругой системы является величиной, постоянной во времени 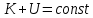 K – кинетическая энергия; U – упругая энергия системы 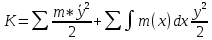   19. Понятие о степенях свободы при динамическом расчете Трудоёмкость динамического расчета упругой системы зависит от её степени свободы.  1 степень свободы 1 степень свободы Количество степеней свободы равно количеству dx Количество степеней свободы равно количеству dx4 степенисвободы Если учитывать собственную распределенную массу упругой системы, то число степеней свободы последней окажется равным бесконечности. Во многих случаях удается свести расчет таких систем к расчету систем с конечным числом степеней свободы. 20. Колебания системы с одной степенью свободы. Дифференциальное уравнение движения масс Рассмотрим невесомую балку с сосредоточенной массойm. К массе приложена сила F(t), явл. функцией времени. 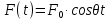 - гармонически изменяющ. сила. В точке прикрепления массы будут действовать две силы. Внешняя сила F(t) и сила инерции - гармонически изменяющ. сила. В точке прикрепления массы будут действовать две силы. Внешняя сила F(t) и сила инерции 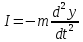 (1). При колебаниях балки возникнут силы сопротивления внешней среды (воздух, вода), которые в первом приближении не будем учитывать. Перемещение массы от двух сил равно (1). При колебаниях балки возникнут силы сопротивления внешней среды (воздух, вода), которые в первом приближении не будем учитывать. Перемещение массы от двух сил равно 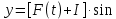 . .С учётом (1) 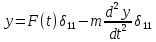 . Разделим каждое слагаемое на ( . Разделим каждое слагаемое на (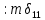 ), получим: ), получим: 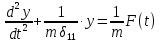 (2). (2).Дифференциальное уравнение движения масс. Интеграл этого уравнения состоит из общего интеграла явл. решением однородного уравнения и частного уравнения, учитывающ. правую часть. 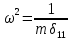 (3) (3) 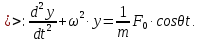 Рассмотрим однородное диф.уравнение 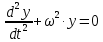 ; ;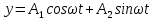 . . Для определения постоянных 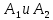 используем начальные условия используем начальные условия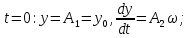   Ч 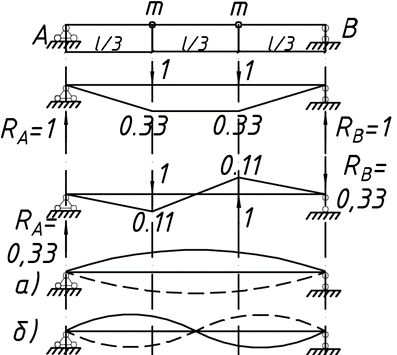 астный интеграл. При астный интеграл. При  .Полный интеграл диф. уравнения: .Полный интеграл диф. уравнения: 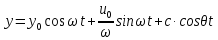 (4). (4). Первые два слагаемых описывают колебания массы при отсутствии внешней силы F(t) и носят название собственных колебаний. Третье слагаемое описывает движение, возникающее под действием силы F(t) и колебаний, назыв. вынужденными. | ||||||||||||||
