1.Множество. Пустое множество. Равные множества. Подмножество.
Множество - это математический объект, сам являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества и обладают общим для всех их характеристическим свойством. Изучением общих свойств множеств занимаются теория множеств, а также смежные разделы математики и математической логики. Примеры: множество жителей заданного города, множество непрерывных функций, множество решений заданного уравнения. Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством. Понятие множества позволяет практически всем разделам математики использовать общую идеологию и терминологию.
Пустое множество - множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойством. Пустое множество является своим (тривиальным) подмножеством, но не является своим элементом. Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Пустое множество — единственное множество, для которого класс множеств, равномощных ему, состоит из единственного элемента (самого́ пустого множества). Также, пустое множество — единственное множество, имеющее ровно 1 подмножество (само себя), и единственное множество, равномощное любому своему подмножеству.
Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. ... если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов.
Подмножество- это понятие части множества. Есть собственные и несобственные подмножества
Любое множество B среди своих подмножеств содержит само себя и пустое множество. Само множество B и пустое множество называют несобственными подмножествами, остальные подмножества называют собственными подмножествами
Множество A называется подмножеством множества B если все элементы, принадлежащие A также принадлежат B.
2. Операции над множествами. Объединение. Пересечение. Разность. Дополнение. Симметрическая разность.
Две самые важные операции, которые выполняются над множествами — это пересечение и объединение.
Пересечение множеств часто записывается с помощью такой нотации: X ∩ Y. Пересечение определяет, где два множества пересекаются. Другими словами, эта операция возвращает все элементы, которые входят в два множества. В нашем примере пересечение Set X и Set Y возвращает все книги, которые человек читал и которые есть у него дома. Хороший ключ к пониманию пересечения — ключевое слово «и». Мы получаем книги, которые человек читал и которые есть у него дома. Несмотря на то, что полученные с помощью пересечения книги существуют в двух множествах, мы не повторяем их, так как в множестве могут быть только уникальные элементы.
Объединение двух множеств обозначается так: X ∪ Y. Объединение возвращает общность двух множеств или объединённое множество. Иными словами, с помощью объединения множеств можно получить новое множество элементов, которые существуют хотя бы в одном исходном множестве. В нашем случае объединение вернёт все книги, которые человек читал, а также все книги, которые есть у него дома. Обратите внимание, если книга входит одновременно в Set X и Set Y, она не может дублироваться в новом множестве после объединения, так как в множества входят только уникальные элементы.
Разность двух множеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств A и B обозначается как A/B но иногда можно встретить обозначение A – B и A B
Множество часто называют дополнением множества B до множества A (только когда множество В полностью принадлежит множеству А)
Симметри́ческая ра́зность двух множеств — теоретико-множественная операция, результатом которой является новое множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Другими словами, если есть два множества A и B , их симметрическая разность есть объединение элементов A, не входящих B с элементами B, е входящими в A. На письме для обозначения симметрической разности множеств A и B используется обозначение A знак треугольника B, реже используется обозначение A – B или A+B
3. Диаграмма Венна
Диаграмма Венна – это диаграмма, которая визуально отображает все возможные логические отношения множеств, каждое из которых, как правило представлено окружностью. Каждое множество представляет собой набор данных, у которых есть между собой нечто общее. Область наложения окружностей известна как «область пересечения» - она отображает данные с общими качествами из всех пересекающихся множеств.
Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов[3], для : описания функционирования формальных нейронов Мак-Каллока и сетей из них синтеза надежных сетей из не вполне надежных элементов, построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств, получения логических следствий из заданной информации, минимизации формул исчислений
4. Мощность множества. Формула включений и исключений.
Мощность множества- характеристика множеств, обобщающая понятие количества элементов конечного множества
В основе этого понятия лежат естественные представления о сравнении множеств:
Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность, равномощны).
Обратно: равномощные множества должны допускать такое взаимно-однозначное соответствие.
Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).
Мощность множеств позволяет сравнивать бесконечные множества.
Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре. Например, в случае двух множеств A,B формула включений-исключений имеет вид: 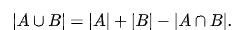

5. Свойства операций над множествами. Алгебра множеств
Сумма ( объединение ) множеств А и В ( пишется А  В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом, е В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом, е 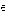 А А  В тогда и только тогда, когда либо е В тогда и только тогда, когда либо е 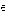 А , либо е А , либо е 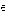 В . В .
Произведение ( пересечение ) множеств А и В ( пишется А  В , рис.2 ) есть множество элементов, каждый из которых принадлежит и А , и В . Таким образом, е В , рис.2 ) есть множество элементов, каждый из которых принадлежит и А , и В . Таким образом, е 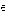 А А  В тогда и только тогда, когда е В тогда и только тогда, когда е 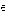 А и е А и е 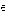 В . В .
Разность множеств А и В ( пишется А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.
Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В )  ( В – А ). ( В – А ).
Свойства операций над множествами:

Алгебра множеств в теории множеств — это непустая система подмножеств некоторого множества X , замкнутая относительно операций дополнения (разности) и объединения (суммы). Алгебра множеств — это частный случай алгебры с единицей, где операцией «умножения» является пересечение множеств, а операцией «сложения» является симметрическая разность.
9. Способы задания бинарного отношения. Задание бинарного отношение с помощью графов.
Пусть А и В — два конечных множества и R — бинарное отношение между ними. Мы изобразим элементы этих множеств точками на плоскости. Для каждой упорядоченной пары отношения R нарисуем стрелку, соединяющую точки, представляющие компоненты пары. Такой объект называется ориентированным графом или орграфом^ точки же, изображающие элементы множеств, принято называть вершинами графа.

10. Способы задания бинарного отношения. Задание бинарного отношения с помощью матриц.
в виде матрицы: пусть A={a1, a2, …, an} и B={b1, b2, …, bm}, r – отношение на A´B. Матричным представлением r называется матрица M=[mij] размера n´m, определенная соотношениями

11. Свойства отношений. Рефлексивность. Симметричность. Кососимметричность. Транзитивность.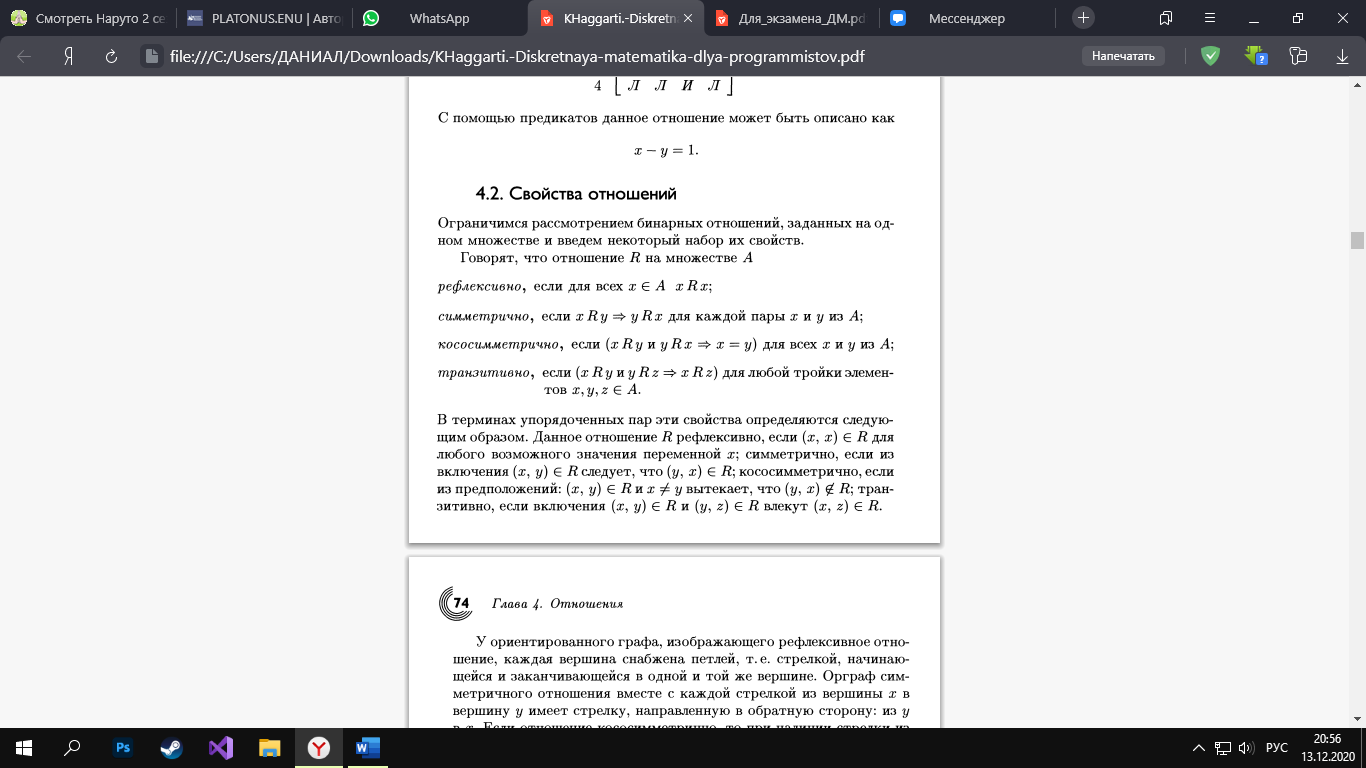
12. Свойства отношений. Замыкание отношения.

13. Отношение эквивалентности. Разбиение множества.
Рефлексивное, симметричное и транзитивное бинарное отношение на множестве А называется отношением эквивалентности. От ношение эквивалентности в некотором смысле обобщает понятие равенства. Эквивалентные элементы (т. е. находившиеся в отношении эквивалентности), как правило, обладают какими-то общими признаками.

14. Отношение частичного порядка. Частично упорядоченное множество.
Диаграмма Хассе.

15. Обратное отношение

16. Композиция отношений. Булево произведение матриц.

Булевы матрицы-это матрицы, каждая запись которых равна 0 или 1, а умножение матриц выполняется с помощью AND Для * и OR для +.
17. Функция. Область определения функции. Область значений функции.


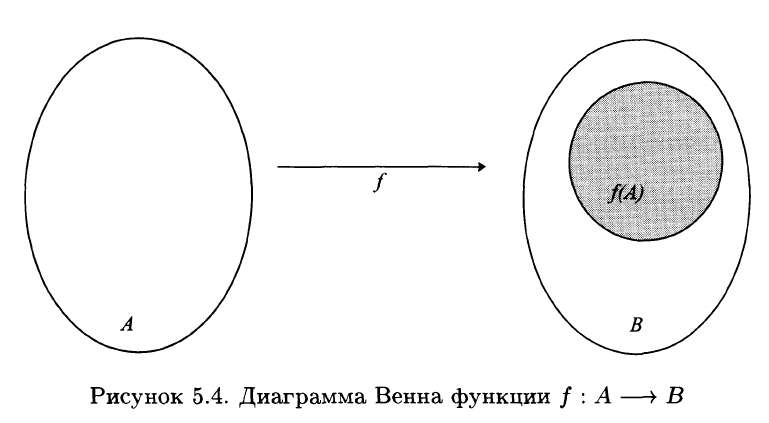
18. Функция. Сюръекция. Инъекция. Биекция.
Инъекция 
Сюръекция

Биекция
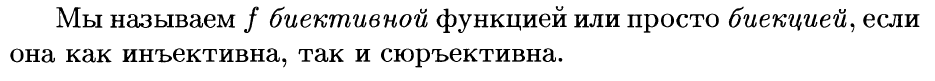
19. Обратная функция. Критерий обратимости.

Критерий

20.Композиция функций.
 
25. Размещение с повторениями. Формула числа размещений с повторениями. -6лек
 
Размещения с повторениями.
Пусть существуют n различных элементов. Выберем из них m штук, действуя по следующему принципу: возьмем любой элемент, но не будем устанавливать его в какой-либо ряд, а просто запишем под номером 1 его название, сам же элемент вернем к остальным элементам. Затем опять из всех n элементов выберем один, запишем его название под номером 2 и снова вернем элемент обратно. Будем выполнять эти операции, пока не получим m названий. Размещения с повторениями вычисляются по формуле
26. Сочетание с повторениями. Формула числа сочетаний с повторениями. -6лек


Сочетания с повторениями.
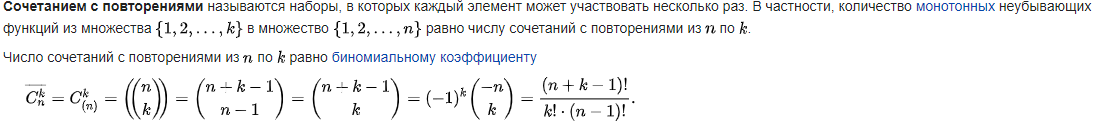
27. Бином Ньютона. Треугольник Паскаля. -6 лек
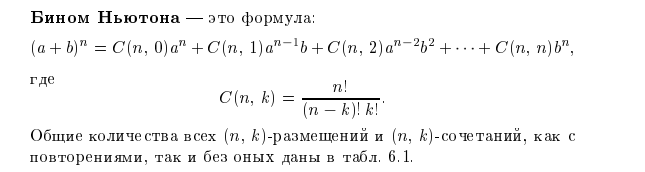


http://www.cleverstudents.ru/expressions/binomial_theorem.html
28. Перестановка (без повторений). Формула числа перестановок. -6лек

Перестановки без повторений.
Перестановки - это комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком расположения этих элементов. Возьмем n различных элементов a1, a2, a3, … an; будем переставлять эти элементы всевозможными способами, оставляя без изменения число элементов и меняя только порядок их расположения. Обозначим общее число полученных таким образом перестановок P(n). P - первая буква французского словаpermutation - перестановка.
Составив таблицу перестановок для n элементов и применив (n - 1) раз правило произведения, получим число всех возможных перестановок:
P(n) = n • (n -1) • (n - 2) • … • 3 • 2 • 1 = n!
Такие перестановки называются перестановками без повторений (один и тот же элемент не может повториться в комбинации, все элементы различны).
32. Связный граф. Алгоритм связности.
33.Гамильтоновы графы.
34.Задача коммивояжера. Алгоритм ближайшего соседа.
 
35. Деревья.
36. Остовное дерево. Алгоритм поиска минимального остовного дерева.
Остовное дерево графа — это дерево, подграф данного графа, с тем же числом вершин, что и у исходного графа. Неформально говоря, остовное дерево получается из исходного графа удалением максимального числа рёбер, входящих в циклы, но без нарушения связности графа. Остовное дерево включает в себя все {\displaystyle n}n вершин исходного графа и содержит {\displaystyle n-1}n- 1 ребро.
Если каждому ребру графа присвоен вес (длина, стоимость и т. п.), то нахождением оптимального остовного дерева, которое минимизирует сумму весов входящих в него рёбер, занимаются многочисленные алгоритмы нахождения минимального остовного дерева.
Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

Или алгоритм Прима:
На вход алгоритма подаётся связный неориентированный граф. Для каждого ребра задаётся его стоимость.
Сначала берётся произвольная вершина и находится ребро, инцидентное данной вершине и обладающее наименьшей стоимостью. Найденное ребро и соединяемые им две вершины образуют дерево. Затем, рассматриваются рёбра графа, один конец которых — уже принадлежащая дереву вершина, а другой — нет; из этих рёбер выбирается ребро наименьшей стоимости. Выбираемое на каждом шаге ребро присоединяется к дереву. Рост дерева происходит до тех пор, пока не будут исчерпаны все вершины исходного графа.
Результатом работы алгоритма является остовное дерево минимальной стоимости.
37. Ориентированные графы.
Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами. Граф, ни одному ребру которого не присвоено направление, называется неориентированным графом или неорграфом.
Формально, орграф {\displaystyle D=(V,E)} D=(V, E) состоит из множества {\displaystyle V}V, элементы которого называются вершинами, и множества {\displaystyle E}E упорядоченных пар вершин {\displaystyle u,v\in V}ᶸ,ᶹͼ(это э наоборот, если что) V.
Дуга {\displaystyle (u,v)}ᶸᶸ,ᶹ инцидентна вершинам ᶸ{\displaystyle u} и ᶹ{\displaystyle v}. При этом говорят, что {\displaystyle u}ᶸ — начальная вершина дуги, а {\displaystyle v}ᶹ — конечная вершина.
Орграф, полученный из простого графа ориентацией рёбер, называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.
Направленный полный граф называется турниром.
Орграфы широко применяются в программировании как способ описания систем со сложными связями. К примеру, одна из основных структур, используемых при разработке компиляторов и вообще для представления компьютерных программ — граф потоков данных.
38. Алгоритм топологической сортировки
Топологическая сортировка - способ нумерации вершин ориентированного графа, при котором каждое ребро ведёт из вершины с меньшим номером в вершину с большим номером.
Для одного графа может существовать несколько спобосов топологической сортировки (например когда он несвязный), а может не существовать не одного (при наличии циклов).
Алгоритм топологической сортировки тривиально определяется через DFS. Будем присваивать номера в убывающем порядке: от самого большого к самому малому. Пусть мы хотим присвоить номер вершине ᶹ Будем работать в обратном порядке: сначала присвоим номера всем дочерним вершинам (рекурсивно), которые их ещё не имеют (некоторые уже могут иметь номера, так как мы могли посетить их раньше). Теперь все дочерние вершины (и, рекурсивно, все их поддеревья) уже пронумерованы. Просто присвоим следующий номер текущей вершине: он будет меньше всех номеров вершин поддерева по определению. Применяем этот алгоритм для всех вершин, ещё не посещённых ранее, по очереди.
39. Пути в орграфах. Матрица достижимости орграфа.
Путь есть маршрут в орграфе без повторяющихся дуг, простой путь — без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой.
Контур есть замкнутый путь.
Для полумаршрута снимается ограничение на направление дуг, аналогично определяются полупуть и полуконтур.
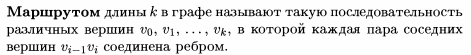
40. Алгоритм Уоршелла.
41. Кратчайший путь. Нагруженный граф. Весовая матрица.


42. Алгоритм Дейкстры.

43.
44. Булева алгебра. Законы булевой алгебры.
Булевой алгеброй называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), и (аналог дизъюнкции), одной унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для любых a, b и c из множества A верны следующие законы:

45. Булева функция.
Булевой функцией от n аргументов называется функция f из n-ой степени множества { 0, 1 } в множество { 0, 1 }.
Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству { 0, 1 }. Множество { 0, 1 } мы будем в дальнейшем обозначать через B.
Булеву функцию от n аргументов можно рассматривать как n-местную алгебраическую операцию на множестве B. При этом алгебра , где W – множество всевозможных булевых функций, называется алгеброй логики.
46. Дизъюнктивная нормальная форма булевой функции.

47. Конъюнктивная нормальная форма булевой функции.

48. Упрощение (минимизация) булевой функции. Карта Карно.
 

49. Функциональные схемы.


50) Полная система булевых функций.
Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций.
Замыканием (англ. сlosure) множества функций называется минимальное по включению замкнутое подмножество всех функций, содержащее данное множество функций.
 |
 Скачать 6.43 Mb.
Скачать 6.43 Mb.