Представление множеств на языке Пролог и операции над ними

• Название: Представление множеств на языке Пролог и операции над ними
• Дата: 11.05.2021
• Размер: 184.36 Kb.
• Имя файла: Kursovaya_Prolog_Nesterov_IE-65-18.docx
• Тип: Курсовая; #203694

ФГБОУ ВО НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

«МЭИ»

«Инженерно-экономический институт»

Курсовая работа

по дисциплине: «Интеллектуальные информационные системы»

Тема: «Представление множеств на языке Пролог и операции над ними»

Студент группы ИЭ-65-18 Нестеров И.М.

(Ф.И.О.)

Руководитель Карпович Е.Е.

(Ф.И.О.)

Сдана на проверку
Возвращена на доработку
Допущена к защите
Оценка

Москва 2021 г.

Оглавление

Введение 3

1. Множества и операции над множествами 4

2. Множества в языке Пролог 5

3. Пересечение множеств в Пролог 6

4. Объединение множеств в Пролог 8

5. Разность множеств в Пролог 10

6. Декартово произведение множеств в Пролог 12

7. Определение подмножества в языке Пролог 14

8. Равенство множеств в языке Пролог 16

9. Техническая часть 17

Заключение 23

Список используемых источников 24

Введение

Множество — одно из ключевых понятий математики; это математический объект, сам являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества и обладают общим для всех их характеристическим свойством.

Изучением общих свойств множеств занимаются теория множеств, а также смежные разделы математики и математической логики. Примеры: множество жителей заданного города, множество непрерывных функций, множество решений заданного уравнения. Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством. Понятие множества позволяет практически всем разделам математики использовать общую идеологию и терминологию.

1. Множества и операции над множествами

• 
  Пересечение множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам. (а)
  
• 
  Объединение множеств (сумма или соединение) — множество, содержащее в себе все элементы исходных множеств. (б)
  
• 
  Разность множеств — операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. (в)
  
• 
  Прямое, или декартово произведение двух множеств — множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств.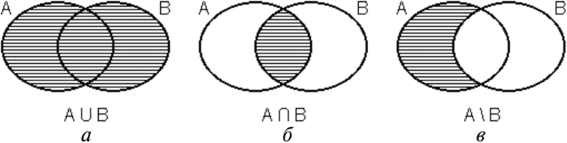
  

Подмножество — это понятие части множества. Множество A является подмножеством множества B, если любой элемент, принадлежащий A также принадлежит B.

Пустое множество — множество, не содержащее ни одного элемента. Пустое множество является своим подмножеством, но не является своим элементом.

Равенство множеств — это утверждение, которое означает, что множества состоят из одних и тех же элементов. Любой элемент множества A принадлежит множеству B и любой элемент множества B принадлежит множеству A.

2. Множества в языке Пролог

В языке Пролог множества представляют в виде списков

Списки — структуры данных, с помощью которых можно представлять множества и графы в программах на языке Пролог. Множества отличаются от списков тем, что в списках могут быть повторяющиеся элементы, а во множествах — нет. С другой стороны, в списках порядок следования элементов имеет значения, а множества могут быть неупорядоченными. В следующих параграфах будут рассмотрены предикаты, выполняющие операции над множествами. ­

Список в Пролог заключается в квадратные скобки и элементы списка разделяются запятыми. Список, который не содержит ни одного элемента, называется пустым списком.

Примеры списков:

список, элементами которого являются целые числа

[1, 2, 3]

список, элементами которого являются символы

[one, two, three]

список, элементами которого являются строки

["One", "Two", "Three"]

пустой список

[ ]

3. Пересечение множеств в Пролог

Предикат interset определяет операцию пересечения двух множеств. Пересечением двух множеств X и Y является множество Z, состоящее из элементов, которые принадлежат и множеству X, и множеству Y одновременно.

Предикат interset (X, Y, Z) — истинен, если множество Z является пересечением множеств X и Y. Схема отношения этого предиката имеет вид:

interset(<список>, <список>, <список>).

Декларативное описание предиката interset (X, Y, Z) формулируется следующим образом:

• 
  Пересечение пустого множества с непустым множеством Х есть пустое множество.
  
• 
  Список, определяющий первое множество Х можно разделить на голову Н и хвост Xs. Если голова первого списка Н принадлежит второму списку Y, то рекурсивно вызывается процедура interset с аргументами Xs и Y. При этом терм H помещается в результирующий список.
  
• 
  Список, определяющий первое множество Х можно разделить на голову Н и хвост Xs. Если голова первого списка Н не принадлежит второму списку Y, то рекурсивно вызывается процедура interset с аргументами Xs и Y. При этом терм H в результирующий список не помещается.
  

Процедура interset(X,Y,Z) состоит из трех правил:

interset([],X,[]).

interset([H|Xs],Y, [H|Z]):-member(H,Y),!,interset(Xs,Y,Z).

interset([H|Xs],Y,Z):-interset(Xs,Y,Z).

Процедура interset выполняется следующим образом:

? — interset([a,b,c],[d,a,b,f],Z).

ТР: interset([a,b,c],[d,a,b,f],Z).

Шаг 1: ТЦ: interset([a,b,c], [d,a,b,f] ,Z).

Пр1: [a,b,c] =[] — неуспех (списки разной длины)

Пр2: interset([a|[b,c]],[d,a,b,f],[a|Z1]):-member(a,[d,a,b,f]),!,interset([b,c], [d,a,b,f],Z1).

при этом Z=[a|Z1]

ТР: member(a,[d,a,b,f]),!,interset([b,c],[d,a,b,f],Z).

Шаг 2: ТЦ: member(a,[d,a,b,f]) — успех

ТР: interset([b,c],[d,a,b,f],Z1).

Шаг 3: ТЦ: interset([b,c],[d,a,b,f],Z1).

Пр1: [b,c] =[] — неуспех (списки разной длины)

Пр2: interset([b|[c]],[d,b,a,f],[b|Z2]):-member(b,[d,a,b,f]),!,interset([c],[d,a,b,f],Z2).

при этом Z1=[b|Z2]

ТР: member(b,[d,a,b,f]),!,interset([c],[d,b,a,f],Z2).

Шаг 4: ТЦ: member(b,[d,a,b,f]) — успех

ТР: interset([c],[ d,a,b,f],Z2).

Шаг 5: ТЦ: interset([c],[ d,a,b,f ],Z2).

Пр1: [c] =[] — неуспех (списки разной длины)

Пр2: interset([c|[]],[d,a,b,f],[c|Z3]):-member(c,[d,a,b,f]),!,interset([],[d,a,b,f],Z3).

ТР: member(c,[d,a,b,f]),!,interset([],[d,a,b,f ],Z3).

Шаг 6: ТЦ: member(с,[d,a,b,f]) — неуспех

Возврат.

Пр3: interset([c|[]],[ d,a,b,f ],Z2):- interset([],[d,a,b,f ],Z2).

ТР: interset([],[d,a,b,f ],Z2).

Шаг 7: ТЦ: interset([],[d,a,b,f ] ,Z2).

Пр1: [] =[]  успех при подстановке Z2=[].

Выход из рекурсии на шаг 3, Z1=[b|Z2] или Z1=[b].

Выход из рекурсии на шаг 1, Z=[a|Z1] или Z=[a|[b]] или Z=[a,b].

ТР: — успех.

Результат вычисления запроса Z=[a,b]. — успех.

4. Объединение множеств в Пролог

Предикат unionset определяет операцию объединения двух множеств. Объединением двух множеств X и Y является множество Z, состоящее из элементов, которые принадлежат или множеству X, или множеству Y, или обоим множествам одновременно.

Предикат unionset (X, Y, Z) — истинен, если множество Z является объединением множеств X и Y. Схема отношения этого предиката имеет вид:

unionset(<список>, <список>, <список>).

Декларативное описание предиката unionset (X, Y, Z) формулируется следующим образом:

• 
  Объединение пустого множества с непустым множеством Х есть множество Х.
  
• 
  Список, определяющий первое множество Х можно разделить на голову Н и хвост Xs. Если голова первого списка Н принадлежит второму списку Y, то рекурсивно вызывается процедура unionset с аргументами Xs и Y. При этом терм H в результирующий список не помещается.
  
• 
  Список, определяющий первое множество Х можно разделить на голову Н и хвост Xs. Если голова первого списка Н не принадлежит второму списку Y, то рекурсивно вызывается процедура unionset с аргументами Xs и Y. При этом терм H помещается в результирующий список.
  

Процедура unuonset(X,Y) состоит из трех правил:

unionset([],X,X).

unionset([H|Xs],Y,Z):-member(H,Y),!,unionset(Xs,Y,Z).

unionset([H|Xs],Y,[H|Z]):-unionset(Xs,Y,Z).

Процедура unionset выполняется следующим образом:

?  unionset([a,b,c],[d,a,b,f],Z).

ТР: unionset([a,b,c],[d,a,b,f],Z).

Шаг 1: ТЦ: unionset([a,b,c], [d,a,b,f] ,Z).

Пр1: [a,b,c] =[] — неуспех (списки разной длины)

Пр2: unionset([a|[b,c]],[d,a,b,f],Z):-member(a,[d,a,b,f]),!,unionset([b,c], [d,a,b,f],Z).

ТР: member(a,[d,a,b,f]),!,unionset([b,c],[d,a,b,f],Z).

Шаг 2: ТЦ: member(a,[d,a,b,f]) — успех

ТР: unionset([b,c],[d,a,b,f],Z1).

Шаг 3: ТЦ: unionset([b,c],[d,a,b,f],Z).

Пр1: [b,c] =[] — неуспех (списки разной длины)

Пр2: unionset([b|[c]],[d,b,a,f],Z):-member(b,[d,a,b,f]),!,unionset([c],[d,a,b,f],Z).

ТР: member(b,[d,a,b,f]),!,unionset([c],[d,b,a,f],Z).

Шаг 4: ТЦ: member(b,[d,a,b,f]) — успех

ТР: unionset([c],[ d,a,b,f],Z).

Шаг 5: ТЦ: unionset([c],[ d,a,b,f ],Z).

Пр1: [c] =[] — неуспех (списки разной длины)

Пр2: unionset([c|[]],[d,a,b,f],Z):-member(c,[d,a,b,f]),!,unionset([],[d,a,b,f],Z).

ТР: member(c,[d,a,b,f]),!,unionset([],[d,a,b,f ],Z).

Шаг 6: ТЦ: member(с,[d,a,b,f]) — неуспех

Возврат.

Пр3: unionset([c|[]],[ d,a,b,f ],[c|Z1]):- unionset([],[d,a,b,f ],Z1).

Z=[c|Z1]

ТР: unionset([],[d,a,b,f ],Z1).

Шаг 7: ТЦ: unionset([],[d,a,b,f ] ,Z1).

Пр1: [] =[] — успех при подстановке Z1=[d,a,b,f ].

Выход из рекурсии на шаг 6, получается подстановка Z=[c|Z1] или Z=[c,d,a,b,f].

Выход из рекурсии на шаг 5, Z=[c,d,a,b,f].

Выход из рекурсии на шаг 3, Z=[c,d,a,b,f].

Выход из рекурсии на шаг 1, Z=[c,d,a,b,f].

ТР: — успех.

Результат вычисления запроса Z=[c,d,a,b,f]. — успех.

5. Разность множеств в Пролог

Предикат difset определяет операцию разности двух множеств. Разностью двух множеств X и Y является множество Z, состоящее из элементов, которые принадлежат множеству X, но не принадлежат множеству Y.

Предикат difset (X, Y, Z) — истинен, если множество Z является разностью множеств X и Y. Схема отношения этого предиката имеет вид:

difset(<список>, <список>, <список>).

Декларативное описание предиката difset (X, Y, Z) формулируется следующим образом:

• 
  Разность пустого множества и непустого множеством Х есть пустое множество.
  
• 
  Список, определяющий первое множество Х можно разделить на голову Н и хвост Xs. Если голова первого списка Н не принадлежит второму списку Y, то рекурсивно вызывается процедура difset с аргументами Xs и Y. При этом терм H помещается в результирующий список.
  
• 
  Список, определяющий первое множество Х можно разделить на голову Н и хвост Xs. Если голова первого списка Н принадлежит второму списку Y, то рекурсивно вызывается процедура difset с аргументами Xs и Y. При этом терм H в результирующий список не помещается.
  

Процедура difset(X,Y,Z) состоит из трех правил:

difset([],X,[]).

difset([H|Xs],Y, [H|Z]):-not(member(H,Y)),!,difset(Xs,Y,Z).

difset([H|Xs],Y,Z):-difset(Xs,Y,Z).

Процедура difset выполняется следующим образом:

? — difset([a,b,c],[d,a,b,f],Z).

ТР: difset([a,b,c],[d,a,b,f],Z).

Шаг 1: ТЦ: difset([a,b,c], [d,a,b,f] ,Z).

Пр1: [a,b,c] =[] — неуспех (списки разной длины)

Пр2: difset([a|[b,c]],[d,a,b,f],[a|Z1]):-not(member(a,[d,a,b,f])),!,difset([b,c], [d,a,b,f],Z1).

при этом Z=[a|Z1]

ТР: not(member(a,[d,a,b,f])),!,difset([b,c],[d,a,b,f],Z).

Шаг 2: ТЦ: not(member(a,[d,a,b,f])) — неуспех

Возврат.

Пр3: difset([a|[b,c]],[d,a,b,f],Z):-difset([b,c], [d,a,b,f],Z).

ТР: difset([b,c],[d,a,b,f],Z).

Шаг 3: ТЦ: difset([b,c],[d,a,b,f],Z).

Пр1: [b,c] =[] — неуспех (списки разной длины)

Пр2: difset([b|[c]],[d,b,a,f],[b|Z1]):-not(member(b,[d,a,b,f])),!,difset([c],[d,a,b,f],Z1).

при этом Z=[b|Z1]

ТР: not(member(b,[d,a,b,f])),!,difset([c],[d,b,a,f],Z1).

Шаг 4: ТЦ: not(member(b,[d,a,b,f])) — неуспех

Возврат.

Пр3: difset([b|c]],[d,a,b,f],Z):-difset([c], [d,a,b,f],Z).

ТР: difset([c],[ d,a,b,f],Z).

Шаг 5: ТЦ: difset([c],[ d,a,b,f ],Z).

Пр1: [c] =[] — неуспех (списки разной длины)

Пр2: difset([c|[]],[d,a,b,f],[c|Z1]):-not(member(c,[d,a,b,f])),!,difset([],[d,a,b,f],Z1).

при этом Z=[c|Z1]

ТР: not(member(c,[d,a,b,f])),!,difset([],[d,a,b,f ],Z2).

Шаг 6: ТЦ: not(member(с,[d,a,b,f])) — успех

Шаг 7: ТЦ: difset([],[d,a,b,f ] ,Z1).

Пр1: [] =[] — успех при подстановке Z1=[].

Выход из рекурсии на шаг 5, Z=[c|Z2] или Z=[c].

Выход из рекурсии на шаг 3, Z=[c].

Выход из рекурсии на шаг 1, Z=[c].

ТР: — успех.

Результат вычисления запроса Z=[c]. — успех.

6. Декартово произведение множеств в Пролог

Предикат dek определяет операцию декартова произведения двух множеств. Декартовым произведением двух множеств X={xi} и Y={yi} является множество Z, состоящее из пар элементов [xi, yi], где xi принадлежат множеству X, а yi принадлежат множеству Y.

Предикат dek (X, Y, Z) — истинен, если множество Z является декартовым произведением множеств X и Y. Схема отношения того предиката имеет вид:

dek(<список>, <список>, <список>).

В процедуре dek используются дополнительные предикаты pro и append. Предикат pro (X, Y, Z) — истинен, если X есть терм, Y={Yi} — множество термов, а Z является множество пар вида [X, Yi], где X есть заданный терм, а Yi — соответствующий элемент множества Y. Схема отношения предиката pro имеет вид:

pro(<терм>, <список>, <список>).

Декларативное определение предиката pro (X, Y, Z) формулируется следующим образом.

• 
  Список Y состоит из одного элемента. Тогда список Z является списком пар вида [X, Yi].
  
• 
  Список, определяющий множество Y можно разделить на голову Н и хвост T. Тогда список Z= [[X, H]|T1], если список список T1 есть результат процедуры pro (X, T, T1].
  
• 
  Декларативное описание предиката dek (X, Y, Z) формулируется следующим образом:
  
• 
  Список X состоит из одного элемента. Тогда список Z является результатом процедуры pro (X, Y, Z1.
  
• 
  Список, определяющий первое множество Х можно разделить на голову X и хвост T1. Если pro (X, Y, T2) и dek (T1, Y, T3) и append (T2, T3, Z) истинны, то Z есть декартово произведение списков X и Y.
  

Процедура pro(X,Y,Z) состоит из двух правил:

pro(X,[Y],[[X,Y]|[]]).

pro(X,[H|T], [[X,H]|T1]):-pro(X,T,T1).

Процедура dek(X,Y,Z) состоит из двух правил:

dek([X|[]],Y,Z):pro(X,Y,Z).

dek([X|T1],Y,Z):-pro(X,Y,T2), dek(T1,Y,T3),

append(T2,T3,Z).

Пример запроса к процедуре pro.

? — pro(4,[1,2,3],Z).

Z=[4,2],[4,3],[4,3]]

Yes

Пример запроса к процедуре dek.

? — dek([4,2][3,5,8],Z).

Z=[[4,3],[4,5],[4,8], [2,3],[2,5],[2,8]]

Yes

7. Определение подмножества в языке Пролог

Предикат subset определяет, является ли множество подмножеством другого множества. Множество X является подмножеством множества Y, если все элементы X, принадлежат множеству Y.

Предикат subset (X, Y) — истинен, если множество X является подмножеством Y. Схема отношения этого предиката имеет вид:

subset(<список>, <список>).

Декларативное описание предиката subset (X, Y) формулируется следующим образом.

• 
  Пустое множество является подмножеством любого множества.
  
• 
  Список, определяющий первое множество Х можно разделить на голову Н и хвост Xs. Множество X есть подмножество Y, если голова первого списка Н принадлежит второму списку Y и Xs есть подмножество множества Y.
  

Процедура subset(X,Y) состоит из двух правил:

subset([],Y).

subset([H|Xs],Y):-member(H,Y),subset(Xs,Y).

Рассмотрим пример запроса к процедуре subset.

Процедура subset выполняется следующим образом:

? — subset([a,b,c],[d,a,b,c,f]).

ТР: subset([a,b,c],[d,a,b,c,f]).

Шаг 1: ТЦ: subset([a,b,c], [d,a,b,c,f]).

Пр1: [a,b,c] =[] — неуспех (списки разной длины)

Пр2: subset([a|[b,c]],[d,a,b,c,f]):-member(a,[d,a,b,f])subset([b,c], [d,a,b,c,f]).

ТР: member(a,[d,a,b,c,f])),subset([b,c],[d,a,b,c,f]).

Шаг 2: ТЦ: member(a,[d,a,b,c,f]) — успех

ТР: subset([b,c],[d,a,b,c,f]).

Шаг 3: ТЦ: subset([b,c],[d,a,b,c,f]).

Пр1: [b,c] =[] — неуспех (списки разной длины)

Пр2: subset([b|[c]],[d,a,b,c,f]):-member(b,[d,a,b,c,f]))subset([c],[d,a,b,c,f]).

ТР: member(b,[d,a,b,c,f])),subset([c],[d,b,a,c,f]).

Шаг 4: ТЦ: member(b,[d,a,b,c,f]) — успех

ТР: subset([c],[ d,a,b,f],Z).

Шаг 5: ТЦ: subset([c],[ d,a,b,c,f ]).

Пр1: [c] =[] — неуспех (списки разной длины)

Пр2: subset([c|[]],[d,a,b,f],[c|Z1]):-member(c,[d,a,b,c,f])),subset([],[d,a,b,c,f]).

ТР: member(c,[d,a,b,c,f])),subset([],[d,a,b,c,f ]).

Шаг 6: ТЦ: member(с,[d,a,b,f,c]) — успех

Шаг 7: ТЦ: subset([],[d,a,b,f ] ).

Пр1: [] =[] — успех.

Выход из рекурсии на шаг 5.

Выход из рекурсии на шаг 3.

Выход из рекурсии на шаг 1.

ТР: — успех.

Результат вычисления запроса — успех.

8. Равенство множеств в языке Пролог

Предикат equalset(X,Y) истинен, если множества X и Y совпадают. Множества X и Y задаются списками атомов.

Предикат equalset(X,Y) задается процедурой equalset(X,Y) subset(X,Y),subset(Y,X).

Процедуру equalset(X, Y) нельзя использовать для порождения множества X. Для этого служит процедура

equalsetl(X,Y):-subsetl(X,Y),subsetl(Y,X).

9. Техническая часть

В качестве технического примера можно привести программу на языке Пролог в которой реализовано:

1. 
   Ввод множеств
   
2. 
   Меню
   
3. 
   Пересечение множеств
   
4. 
   Объединение множеств
   
5. 
   Разность множеств
   
6. 
   Декартово произведение множеств
   
7. 
   Проверка на подмножество
   
8. 
   Проверка на равенство множеств
   
9. 
   Обработчик ошибок
   

Код программы:

pr:-write('Введите множество L:'),nl,

read(L),nl,

write('Множество L='),

tab(2), write(L),nl,

write('Введите множество M:'),nl,

read(M),nl,

write('Множество M='),

tab(2), write(M),nl,

write(' Меню '),nl,

write('1. Пересечение множеств '),nl,

write('2. Обьединение множеств '),nl,

write('3. Разность множеств '),nl,

write('4. Декартово произведение множеств '),nl,

write('5. Проверка на подмножество '),nl,

write('6. Проверка на равенство множеств '),nl,

write('Введите номер: '),nl,

read(X),nl,

func(L,M,X).

func(L,M,X):-X=1,!, write("Пересечение множеств: "), interset(L,M,Z), write(Z).

func(L,M,X):-X=2,!, write("Обьединение множеств: "), unionset(L,M,Z), write(Z).

func(L,M,X):-X=3,!, write("Разность множеств: "), difset(L,M,Z), write(Z).

func(L,M,X):-X=4,!, write("Декартово произведение множеств: "), dek(L,M,Z), write(Z).

func(L,M,X):-X=5,!, write("Является ли M подмножеством L: "), subset(L,M).

func(L,M,X):-X=6,!, write("Равны ли множества: "), equalset(L,M).

func(L,M,X):- write("ОШИБКА!").

interset([],X,[]).

interset([H|Xs],Y, [H|Z]):-member(H,Y),!,interset(Xs,Y,Z).

interset([H|Xs],Y,Z):-interset(Xs,Y,Z).

unionset([],X,X).

unionset([H|Xs],Y,Z):-member(H,Y),!,unionset(Xs,Y,Z).

unionset([H|Xs],Y,[H|Z]):-unionset(Xs,Y,Z).

difset([],X,[]).

difset([H|Xs],Y, [H|Z]):-not(member(H,Y)),!,difset(Xs,Y,Z).

difset([H|Xs],Y,Z):-difset(Xs,Y,Z).

append1([],L,L).

append1([H|L],M,[H|R]):- append1(L,M,R).

pro(X,[Y],[[X,Y]|[]]).

pro(X,[H|T], [[X,H]|T1]):-pro(X,T,T1).

dek([X|[]],Y,Z):-pro(X,Y,Z).

dek([X|T1],Y,Z):-pro(X,Y,T2),dek(T1,Y,T3),append1(T2,T3,Z).

subset([],Y).

subset([H|Xs],Y):-member(H,Y),subset(Xs,Y).

equalset(X,Y):-subset(X,Y),subset(Y,X).

Демонстрация работы программы:

Ввод множеств:



Меню:



Пересечение множеств:



Объединение множеств:



Разность множеств:



Декартово произведение множеств:



Проверка на подмножество:



Проверка на равенство множеств:



Обработчик ошибок:

Заключение

Теория множеств используется в разных областях информатики. Это важная для программистов концепция, понимание которой помогает разработчикам эффективно работать с данными.

В свою очередь язык программирования Пролог предоставляет пользователю удобную и функциональную среду и инструменты для работы с различными множествами.

Список используемых источников

1. 
   Интернет – ресурс википедия «Множество»: https://ru.wikipedia.org/wiki/Множество#Некоторые_виды_множеств_и_сходных_объектов
   
2. 
   Карпович Е.Е. Программирование на языке Пролог. Учебное пособие, часть 1. -М.: МГГУ, 2002 г., с. 97.
   
3. 
   Набебин А.А. Н134 Логика и Пролог в дискретной математике. - М.: Издательство МЭИ, 1996. - 452 с.; ил. ISBN 5-7046-0162-6