ИДЗ по физике. ИДЗ2. 1. На диаграмме v T

• Название: 1. На диаграмме v T
• Анкор: ИДЗ по физике
• Дата: 25.06.2021
• Размер: 402.5 Kb.
• Имя файла: ИДЗ2.doc
• Тип: Решение; #221574

1. На диаграмме V – T изображен процесс, который произошел с идеальным газом при постоянном давлении и постоянном объеме. Как при этом изменилась масса газа? (Во сколько раз увеличилась или уменьшилась?)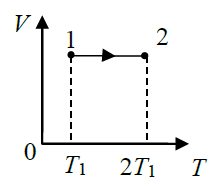



Дано:



Найти:

– ?

Решение

Запишем уравнение Менделеева – Клапейрона для двух состояний газа, учитывая, что согласно условию задачи и :

(1)

(2)

– давление газа; – объем газа; – молярная масса газа; – начальная масса газа; – конечная масса газа; – универсальная газовая постоянная; – начальная температура газа; – конечная температура газа.

Из уравнений (1) и (2) можем записать:



Отсюда:

(3)

Подставим данные в (3):



Ответ: (Масса уменьшилась в 2 раза).

2. Два баллона с объемами V1 и V2 = 2V1 соединены трубкой с краном. Баллоны заполнены воздухом при давлении р1 = 0,3 МПа и р2 соответственно, и одинаковой температуре. Если кран открыть, то в баллонах установится давление 0,5 МПа. Чему равно давление воздуха во втором баллоне (в МПа)?

Дано:









Найти:



Решение

Запишем уравнение Менделеева – Клапейрона для газа первого и второго баллона, до открытия крана, учитывая, что согласно условию задачи температура в них одинакова:

(1)

(2)

и – соответственно давление газа в первом и втором баллоне; и – соответственно объем первого и второго газа; – молярная масса газа; и – соответственно масса газа в первом и втором баллоне; – универсальная газовая постоянная; –температура газа.

Запишем уравнение Менделеева – Клапейрона для газа, когда открыли кран, учитывая, что температура не изменилась:

(3)

Из уравнение (1) находим:

(4)

Из уравнение (2) находим:
(5)

Подставим (4) и (5) в (3):

(5)


Отсюда:



Учитывая, что , получаем:



(6)

Подставим данные в (6):


Ответ: .

3. Определите среднюю кинетическую энергию поступательного движения и полную кинетическую энергию одной молекулы азота при температуре 600 К.

Дано:



Найти:





Решение

Средняя кинетическая энергия поступательного движения одной молекулы равна:

(1)

Где – поступательные степени свободы молекулы. В нашем случае , так как возможны три поступательных движения; – постоянная Больцмана.

Средняя энергия вращательного движения равна:

(2)

– вращательные степени свободы молекулы. В нашем случае .

Тогда среднее значение полной кинетической энергии молекулы равно:



(3)

Подставим данные в (1) и (3):





Ответ: ;

5. Водород занимает объем при давлении р1 = 100 кПа. Газ нагрели при постоянном объеме до давления р2 = 300 кПа. Определите изменение внутренней энергии U газа, работу газа А, теплоту Q, сообщенную газу.

Дано:









Найти:







Решение
Согласно первому началу термодинамики, количество теплоты , полученное газом, расходуется на изменение внутренней энергии ΔU и совершение газом работы А против внешних сил:

(1)

При изохорическом процессе работа равна нулю . В этом случае уравнение (1) запишется так:

₍₂₎

Известно, что изменение внутренней энергии для любого термодинамического процесса равно:

Изменение внутренней энергии равно:

(3)

где – число степеней свободы; – молярная масса газа; – масса газа; – универсальная газовая постоянная; – начальная температура газа; – конечная температура газа.

Запишем уравнение Менделеева-Клайперона:

(4)

Где – молярная масса газа; – масса газа; – давление газа; – универсальная газовая постоянная; – объем газа; – температура газа.
Запишем уравнение (4) сначала для состояния 1, а потом для состояния 2, учитывая, что :
(5)

(6)
Из уравнений (5) и (6) можем записать:



Или

(7)
Учитывая (7), выражение (3) можем записать так:

(8)

Учитывая (7), выражение (2) можем записать так:

(9)

Подставим данные в (9), учитывая, что для двухатомной молекулы, какой является молекула водорода i=5. 



Ответ: ; .
6. Найдите показатель адиабаты для смеси газов, содержащей гелий массой m1 = 10 г и водород массой m2 = 4 г.

Дано:









Найти:

– ?

Решение
Показатель адиабаты можно выразить формулой:

(1)

Где – удельная теплоемкость при постоянном давлении газовой смеси; – удельная теплоемкость при постоянном объеме газовой смеси.

Количество теплоты, необходимое для нагревания смеси газов при постоянном давлении на некоторую температуру определяется формулой:

(2)

Где – удельная теплоемкость при постоянном давлении газовой смеси; и – соответственно массы первого и второго газа в смеси.

С другой стороны это количество теплоты можем записать так:

(3)

Где – удельная теплоемкость при постоянном давлении первого газа; – удельная теплоемкость при постоянном давлении второго газа.

Из уравнений (2) и (3) можем записать:



Отсюда:

(4)

Удельная теплоемкость газа при постоянном давлении определяется формулой:

(5)

где R =8,31 Дж/(моль⋅К) газовая постоянная;  – молярная масса газа; где  i – число степеней свободы.

Запишем выражение (5) отдельно для двух газов:

(6)

(7)

где   – число степеней свободы гелия; – число степеней свободы водорода.

Подставим выражения (6) и (7) в (4):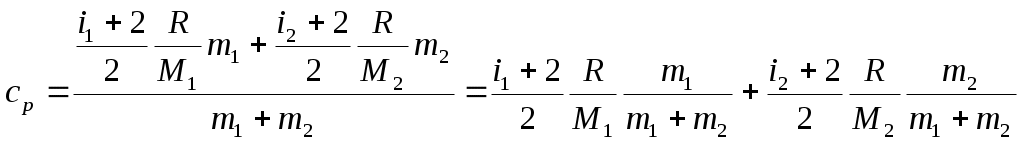



(8)
Количество теплоты, необходимое для нагревания смеси газов при постоянном объеме на некоторую температуру определяется формулой:

(9)

Где – удельная теплоемкость при постоянном объеме газовой смеси.

С другой стороны это количество теплоты можем записать так:

(10)

Где – удельная теплоемкость при постоянном объеме первого газа; – удельная теплоемкость при постоянном объеме второго газа.

Из уравнений (9) и (10) можем записать:



Отсюда:

(11)

Удельная теплоемкость газа при постоянном объеме определяется формулой:

(12)

Запишем выражение (12) отдельно для двух газов:

(13)

(14)

где   – число степеней свободы гелия; – число степеней свободы водорода.

Подставим выражения (13) и (14) в (11):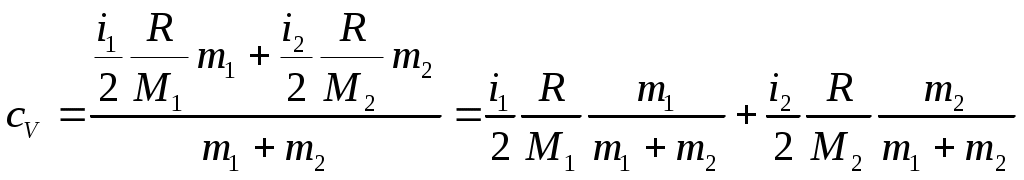

(15)



(16)

Подставим выражения (8) и (16) в (1):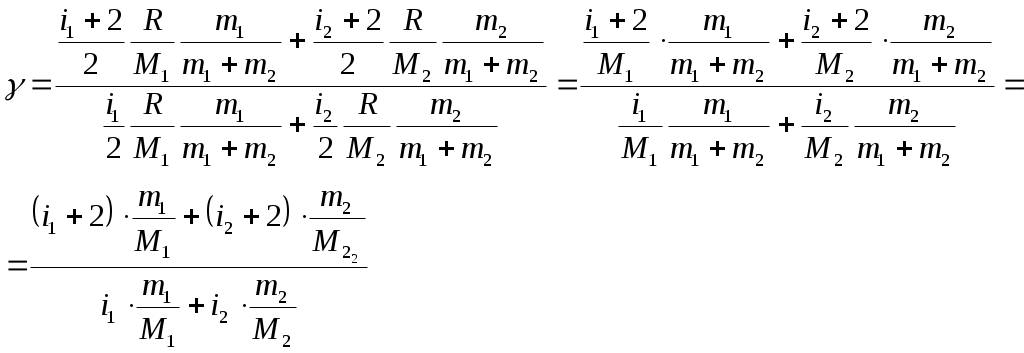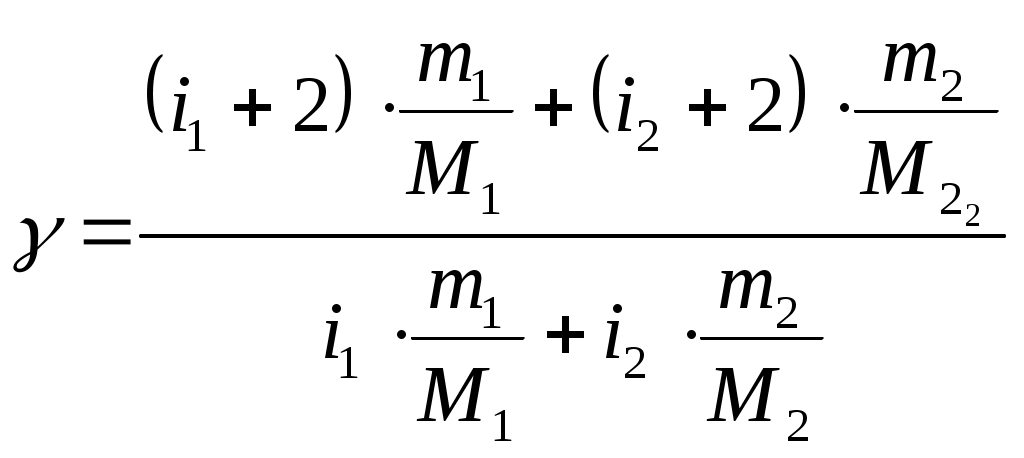


(17)

Подставим данные в формулу (17), учитывая, что для гелия количество степеней свободы равно 3: 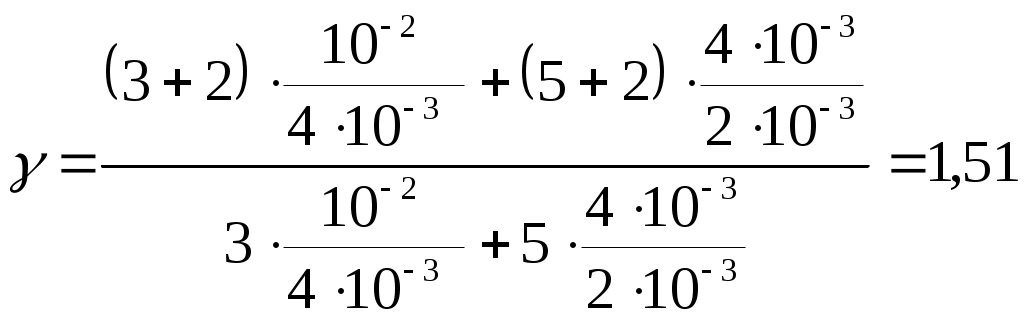, а для водорода :



Ответ: .

7. Температура нагревателя тепловой машины 500 К. Температура холодильника 400К. Определите КПД тепловой машины, работающей по циклу Карно, и полезную мощность машины, если нагреватель ежесекундно передает ей 1675 Дж теплоты.

Дано:









Найти:





Решение

Термический к.п.д. цикла Карно можно определить по формуле:

(1)

где   – абсолютная температура нагревателя;   – абсолютная температура холодильника.
К.п.д. цикла Карно также можно определить по формуле:

(2)

– тепло, подведённое в цикле к рабочему телу;   – тепло, отданное в цикле рабочим телом.

Работа, совершенная рабочим телом тепловой машины равна:

(3)

Подставим выражение (3) в (2):

(4)

Отсюда:

(5)

Работа в единицу времени и есть мощность. Тогда полезная мощность тепловой машины при найденном нами её КПД может быть выражено следующим образом:

(6)

Подставим (1) в (6):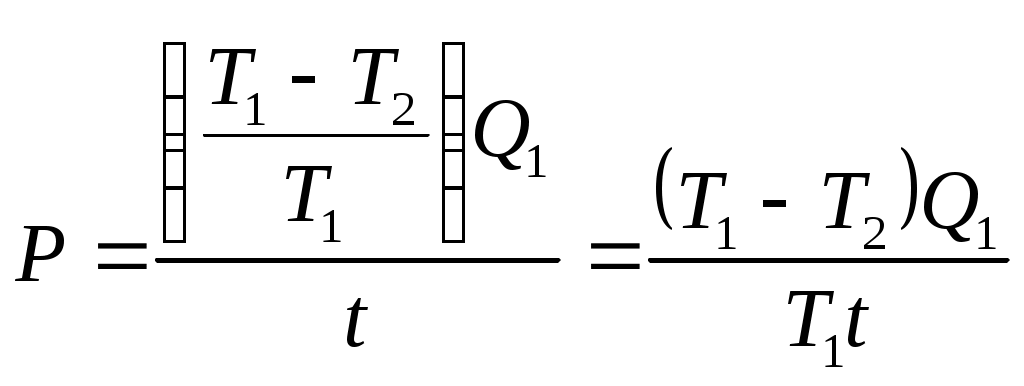


(7)

Подставим данные в (1) и (7):




Ответ: ; .


8. Кислород массой m = 2 кг увеличил свой объем в 5 раз сначала изотермически, затем – адиабатно. Найдите изменение энтропии.

Дано:







Найти:



Решение

Так как энтропия величина аддитивная, то общее изменение энтропии будет равно:

(1)

Где – изменение энтропии при изотермическом процессе; – изменение энтропии при адиабатическом процессе.

По определению, изменение энтропии при переходе системы из состояния 1 в состояние 2 равно:

(2)

где dQ – количества тепла, сообщенное газу, Т – абсолютная температура, S₁ и S₂ – значения энтропии в начальном и конечном состояниях системы.

Поскольку при адиабатическом процессе , то выражение (1) запишем так:

(3)

Найдем изменение энтропии при изотермическом процессе. Согласно первому началу термодинамики, количество теплоты  , полученное газом, расходуется на изменение внутренней энергии  и совершение газом работы   против внешних сил:

(4)

Для изотермического процесса , поэтому согласно первому закону термодинамики

все подводимое количество теплоты идет на работу по расширению, т.е.

dQ = dA = pdV (5)

Запишем уравнение Менделеева-Клайперона:

(6)

Где – молярная масса газа; – масса газа; – давление газа; – универсальная газовая постоянная; – объем газа; – температура газа.
Из уравнения (6) можем записать: 

(7)

Подставим (7) в (5):

(8)

Подставляя (8) в (2), получим:



(9)

Подставим данные в (9):


Ответ: .