Вынужденные колебания струны. 1 Некоторые аналитические результаты о колебаниях натянутого провода

• Название: 1 Некоторые аналитические результаты о колебаниях натянутого провода
• Дата: 21.12.2021
• Размер: 277 Kb.
• Имя файла: Вынужденные колебания струны.doc
• Тип: Документы; #312607

1.1.Некоторые аналитические результаты о колебаниях натянутого провода

1.1.1.Свободные колебания

Контактная подвеска представляет собой пространственную висячую систему проводов, к которой приложены растягивающие силы, создающие натяжение несущего троса и контактного провода, и силы, вызывающие прогиб и смещение проводов в пространстве. Если силы, действующие на подвеску, не зависят от времени, то она находится в положении статического равновесия. Однако в процессе эксплуатации возникают и динамические нагрузки, например, ветровая нагрузка, колебания, вызванные взаимодействием с подвижным составом и др. Для надежной работы всей системы необходимо знать реакцию подвески на динамическое возбуждение того или иного рода.

В качестве математической модели для расчета динамики, как уже было подчеркнуто в п. Error: Reference source not found, можно выбрать модель стержня или натянутой струны. Они описываются уравнениями, содержащими производные по пространственным переменным соответственно четвертого или второго порядка. Понятно, что вычислительная трудоемкость этих моделей будет различна, поэтому обоснованный выбор одной из них очень важен. С этой целью в данном разделе будут рассмотрены некоторые модельные задачи, в которых можно увидеть различия в результатах, полученных при использовании данных моделей. Рассмотрим в качестве первой задачу о свободных колебаниях провода, моделируемого с помощью натянутой струны тил стержня.

Уравнение динамики стержня в отсутствии внешней нагрузки запишется следующим образом

(Некоторые аналитические результаты о колебаниях натянутого провода.1)

Здесь m – погонная масса стержня, Е – модуль Юнга, I – момент инерции поперечного сечения, Т – натяжение, D – демпфирование. Разделим обе части на m и введем величины



Величина а характеризует влияние изгибной жесткости, а с представляет собой скорость распространения малых возмущений вдоль провода.

С учетом введенных обозначений уравнение (Некоторые аналитические результаты о колебаниях натянутого провода.1) перепишется в виде

(Некоторые аналитические результаты о колебаниях натянутого провода.2)

Данное уравнение было решено в работе [14], однако при этом отсутствовало слагаемое, связанное с демпфированием.

Сделаем замену зависимой переменной по формуле . Получим

(Некоторые аналитические результаты о колебаниях натянутого провода.3)

Будем искать решение методом разделения переменных. Сначала найдем частное решение вида

(Некоторые аналитические результаты о колебаниях натянутого провода.4)

Положим и подставим (Некоторые аналитические результаты о колебаниях натянутого провода.4) в уравнение (Некоторые аналитические результаты о колебаниях натянутого провода.3). Получим обыкновенное дифференциальное уравнение (штрихами обозначены производные по х)



Подставляя , будем иметь биквадратное уравнение для определения r



Его корни вычисляются по формулам





Теперь можно записать для Х(х)

(Некоторые аналитические результаты о колебаниях натянутого провода.5)

Для того чтобы найти входящие сюда постоянные, надо конктретизировать граничные условия. Примем, что стержень шарнирно оперт на концах, то есть заданы условия



Отсюда следуют условия для Х(х)



Подставляя сюда (Некоторые аналитические результаты о колебаниях натянутого провода.5), получим . Из последнего равенства вытекает и, следовательно,



С учетом выражения для q, вытекающего из формулы для r_3,4, получим



Отсюда выразим ω (так как эта величина будет зависеть от j, то снабдим ее соответствующим индексом)

(Некоторые аналитические результаты о колебаниях натянутого провода.6)

где обозначено

(Некоторые аналитические результаты о колебаниях натянутого провода.7)

Общее решение однородного уравнения

(Некоторые аналитические результаты о колебаниях натянутого провода.8)

Постоянные A_j и B_j находятся из начальных условий

(Некоторые аналитические результаты о колебаниях натянутого провода.9)

Заметим, что если β=0, то полученное решение совпадает с решением из [14]. Если положить а=0, получим решение волнового уравнения с демпфирующим слагаемым (телеграфное уравнение). Наконец, если и β=0, и а=0 будем иметь решение известного волнового уравнения.

Если затухание достаточно велико, то выражение под корнем в (Некоторые аналитические результаты о колебаниях натянутого провода.6) может стать отрицательным и тогда решение будет чисто затухающим. Однако обычно для подвески величина β не настолько велика [3], поэтому далее этот случай рассматриваться не будет.

Подчеркнем, что полученное решение (Некоторые аналитические результаты о колебаниях натянутого провода.8) имеет одинаковый вид как для стержня так и для струны. Разница заключается лишь в выражении (Некоторые аналитические результаты о колебаниях натянутого провода.7) для μ_j. Таким образом, оценить влияние изгибной жесткости на решение можно рассмотрев величины слагаемых, составляющих выражение (Некоторые аналитические результаты о колебаниях натянутого провода.7).

Для этого примем следующие параметры подвески:

погонная масса m=1.068 кг/м

модуль упругости Е=108.4·10⁹ Па

диаметр провода d=1.237·10^-2 м

момент инерции сечения I=πd⁴/64=1.150·10^-9 м⁴

сила натяжения T=20000 Н

длина провода L=65 м

Подставляя данные величины в (Некоторые аналитические результаты о колебаниях натянутого провода.7), получим



Отсюда следует, что лишь при j порядка сотен первое слагаемое (связанное с изгибной жесткостью) становится сравнимым со вторым. В то же время из литературы известно, что подвеска представляет собой низкочастотную систему. Так из иллюстраций, приведенных в книге [15] (стр. 462, 463), видно, что в зависимости от конструкции подвески заметное влияние на нее оказывают частоты не более 12 – 20 Гц. Таким образом для подвески можно пренебречь первым слагаемым и рассматривать ее как натянутую струну.

Остановимся еще на вопросе о дисперсии волновых решений, связанных с уравнением (Некоторые аналитические результаты о колебаниях натянутого провода.2). Подставим в него (при β=0) решение вида бегущей волны . В результате получим дисперсионное соотношение , откуда фазовая скорость волны . Отсюда следует, что для стержня фазовая скорость зависит от частоты (имеет место дисперсия), причем высокочастотные гармоники опережают низкочастотные. Для струны (а=0) дисперсия отсутствует V_ф=с.

Проиллюстрируем изложенное в данном параграфе конкретным примером. Пусть в начальный момент времени t=0 провод находится в покое и в некоторой точке х=х₀ к нему прикладывается импульс величины S. Последнее означает, что начальная поперечная скорость провода в точке х=х₀ равна V₀=S/m. Соответствующие начальные условия запишутся в виде

,

где δ – дельта-функция, определяемая свойством



для любой непрерывной функции f.

Постоянные А_j, B_j найдутся по формулам (Некоторые аналитические результаты о колебаниях натянутого провода.9)



Решение будет иметь вид



На Рис. Некоторые аналитические результаты о колебаниях натянутого провода.1 показано решение, сосчитанное по данной формуле. Красным цветом нанесено решение для струны, а синим – для стержня.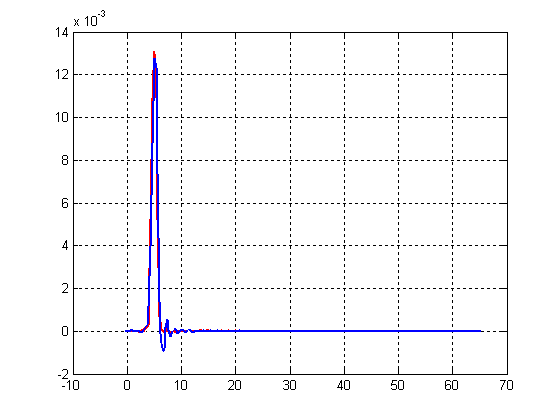


x м

u м


Рис. Некоторые аналитические результаты о колебаниях натянутого провода.1

Видно, что они совпадают, но для стержня явно видна дисперсия, выражающаяся в опережающем распространении высокочастотных гармоник.

1.1.2.Вынужденные колебания под действием сосредоточенной движущейся нагрузки

Рассмотрим теперь действие на провод сосредоточенной нагрузки, движущейся с постоянной скоростью V. Оно будет описываться неоднородным уравнением (Некоторые аналитические результаты о колебаниях натянутого провода.2)(Некоторые аналитические результаты о колебаниях натянутого провода.2)

(Некоторые аналитические результаты о колебаниях натянутого провода.10)

Здесь F – величина приложенной нагрузки, отнесенная к погонной массе провода, х₀ – положение нагрузки в момент t=0,

Будем искать решение уравнения (Некоторые аналитические результаты о колебаниях натянутого провода.10) в виде

(Некоторые аналитические результаты о колебаниях натянутого провода.11)

Подставляя его в уравнение, умножая обе части на и интегрируя от 0 до L, с учетом ортогональности собственных функций, получим обыкновенное дифференциальное уравнение для функции U (точками обозначено дифференцирование по времени)

(Некоторые аналитические результаты о колебаниях натянутого провода.12)

Так как решение однородного уравнения при наличии демпфирования затухает, то со временем остаются только вынужденные колебания, которые определяются частным решением неоднородного уравнения. Оно будет иметь вид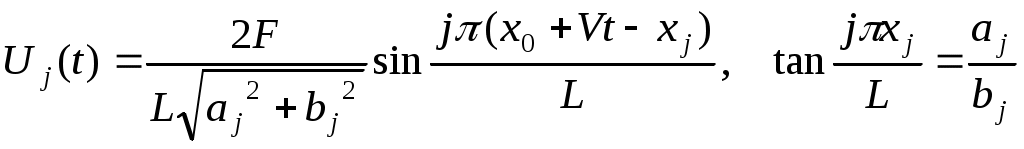

(Некоторые аналитические результаты о колебаниях натянутого провода.13)

где обозначено



Вследствие наличия демпфирования знаменатель не обращается в ноль. Однако можно говорить о его минимальном значении, которое достигается при условии b_j=0, откуда получаем значение критической (резонансной) скорости



Как уже обсуждалось выше, первое слагаемое в этой формуле при умеренных j значительно больше второго, поэтому практически остается одна критическая скорость V_c=c.

Представляет интерес рассмотреть поведение провода при движении нагрузки со скоростью, близкой к критической. Выберем модель струны (a=0) без затухания (β=0), скорость движения нагрузки V=c, в начальный момент времени нагрузка прилагается в точке х₀=0. Тогда уравнение (Некоторые аналитические результаты о колебаниях натянутого провода.12) примет вид



Из него видно, что все гармоники находятся в условиях резонанса. Решение при нулевых начальных условиях имеет вид



Оно содержит так называемый вековой член (второе слагаемое), который стремится к бесконечности при возрастании t. Однако, если скорость движения нагрузки достаточно велика, то перемещение не успевает заметно возрасти за то время, когда нагрузка проходит весь пролет. Заметим, что характер поперечных перемещений провода сильно зависит от скорости движения нагрузки. На Рис. Некоторые аналитические результаты о колебаниях натянутого провода.2 показаны конфигурации провода в момент когда нагрузка пересекает середину пролета при разных скоростях движения.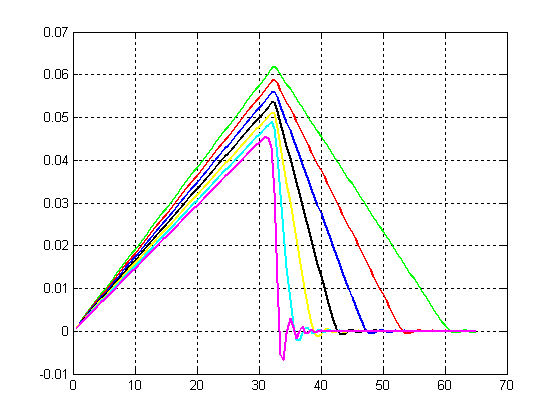


V=70м/с

V=80м/с

V=90м/с

V=100м/с

V=110м/с

V=120м/с

V=130м/с

x м

u м


Рис. Некоторые аналитические результаты о колебаниях натянутого провода.2

Видно, что при приближении скорости к критической наклон провода в месте действия нагрузки увеличивается и становится бесконечным при совпадении скоростей.

Представляет интерес рассмотреть перемещения провода при движении нагрузки со скоростью больше критической. На Рис. Некоторые аналитические результаты о колебаниях натянутого провода.3 приведена конфигурация провода при движении нагрузки с докритической скоростью. Точкой показано местоположение нагрузки. Видно, что максимальное отклонение достигается в месте действия нагрузки.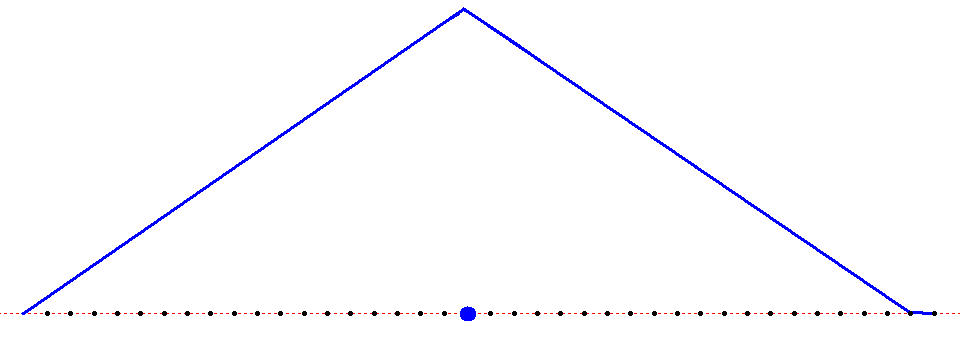



Рис. Некоторые аналитические результаты о колебаниях натянутого провода.3. Докритическая скорость, V=70м/с

На Рис. Некоторые аналитические результаты о колебаниях натянутого провода.4 скорость близка к критической, но меньше ее. Видно, что максимальное отклонение все еще в месте приложения нагрузки.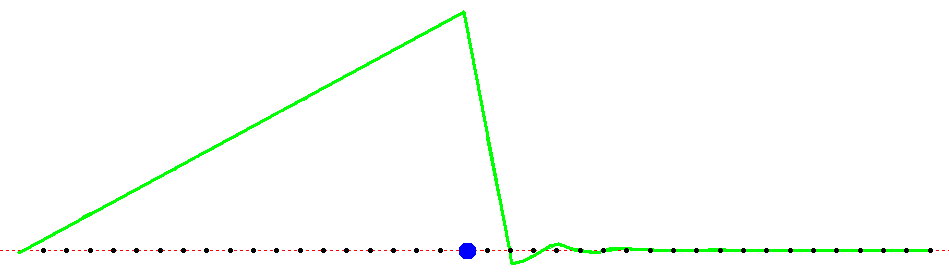



Рис. Некоторые аналитические результаты о колебаниях натянутого провода.4. Почти критическая скорость, V=130м/с

На Рис. Некоторые аналитические результаты о колебаниях натянутого провода.5 приведено решение для закритической скорости. Здесь мы видим, что нагрузка движется быстрее, чем распространяются возмущения вдоль провода, поэтому точка максимального отклонения отстает от точки приложения нагрузки.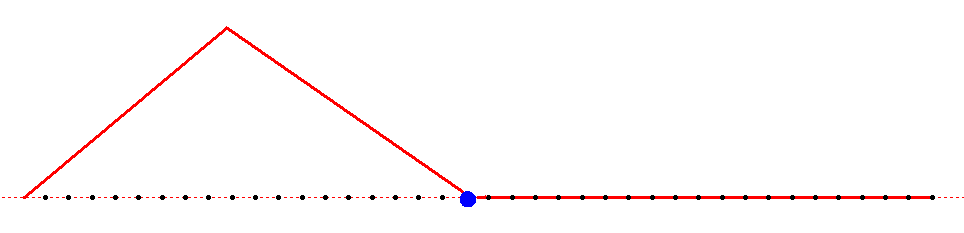



Рис. Некоторые аналитические результаты о колебаниях натянутого провода.5. Закритическая скорость, V=200м/с

Проиллюстрируем влияние изгибной жесткости на решение, изменяя модуль Юнга провода Е. Результаты расчета приведены на Рис. Некоторые аналитические результаты о колебаниях натянутого провода.6. Здесь показана конфигурация провода при разных значениях величины Е в момент прохождения нагрузкой середины пролета. Видно, что положения провода для 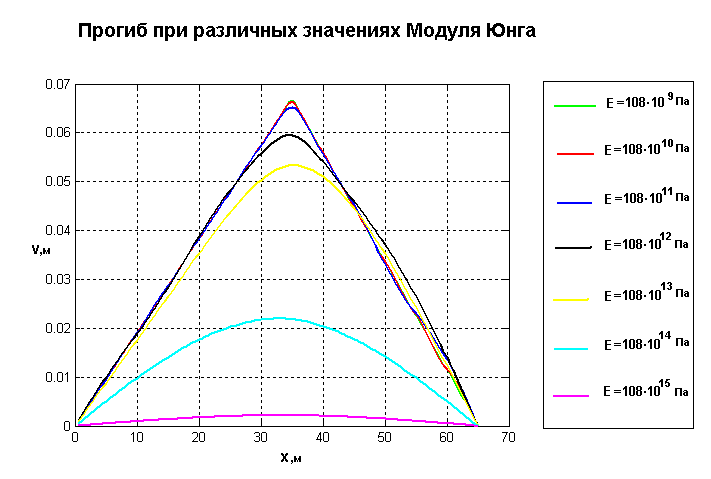и практически сливаются. Более того, если рассмотреть решение для и решение при , то их максимальное отличие за время прохождения нагрузкой целого пролета составит лишь 0.00068 м. Изгиб стержня начинает заметно проявляться только при значениях Е на два порядка превышающих заданное.



Рис. Некоторые аналитические результаты о колебаниях натянутого провода.6

В связи с данным рисунком приведем цитату из статьи [2]: “The model of the string shows the well-known effect that due to the lack of bending stiffness a discontinuity in slope occurs at the point of application of a concentrated force”. По данной причине авторы считают необходимым рассматривать провод как стержень, чтобы учесть изгибную жесткость. Да, для стержня первая производная не рвется в упомянутой точке (рвется лишь третья). Однако из-за малой по сравнению с продольным натяжением изгибающей силы кривизна провода-стержня в точке приложения концентрированной нагрузки столь велика, что неотличима от излома струны с тем же модулем упругости, поэтому учитывать ее нет никакой необходимости. В связи со сказанным далее будет рассматриваться только волновое уравнение, то есть в качестве математической модели проводов, составляющих контактную сеть, будет использоваться натянутая струна или, что то же самое, нить.

1.1.3.Вынужденные колебания под действием движущейся осциллирующей нагрузки

Представляет интерес кроме постоянной движущейся нагрузки рассмотреть осциллирующую нагрузку. Такая нагрузка может возникать, например, при воздействии ветра или со стороны пантографа при колебаниях основания, на котором он закреплен. Ограничимся случаем натянутой струны, подверженной синусоидальной нагрузке. Таким образом будем рассматривать уравнение



Как и выше, будем искать решение в виде (Некоторые аналитические результаты о колебаниях натянутого провода.11). При этом для U(t) получим, аналогично (Некоторые аналитические результаты о колебаниях натянутого провода.12), следующее уравнение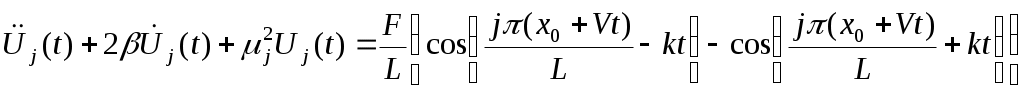



Частное решение неоднородного уравнения есть линейная комбинация синусов и косинусов от аргументов . Вследствие громоздкости оно здесь не приводится. Заметим только, что резонанс имеет место при выполнении соотношений . Отсюда с учетом выражения для μ_j получим значения критической скорости . Из данного равенства видно, что есть две критические скорости, одна из которых выше, а другая ниже, чем в случае постоянной нагрузки. Наименьшая критическая скорость равна . Она даже может стать нулевой при . Для указанных ранее параметров подвески эта частота приблизительно составляет 2π Гц.

Список литературы

1. Poetch G., Evans J., Meisinger R., Kortum W., Krabacher W.: Pantograph/Catenary Dynamics and Control // Vehicle System Dynamics, 28(2-3), 1988, pp.159-195.

2. Petry K., Wallaschek J.: Analitical Models for Dynamics of Catenary/Pantograph // Z. Angew. Math. Mech., 76, 1966, s5, pp.381-382.

3. Simeon B., Arnold M.: Coupling DAEs and PDEs for Simulating the Interaction of Pantograph and Catenary // Mathematical and Computer Modelling of Dynamical Systems, vol.6, 2000, 2, pp.129-144.

4. Collina A., Bruni S.: Numerical Simulation of Pantograph-Overhead Equipment Interaction // Vehicle System Dynamics, 2002, vol.38, 4, pp.261-291.

5. Jong-Hwi Seo, Seo-Won Kim, Il-Ho Jung, Tae-Won Park, Jin-Yong Mok, Young-Guk Kim, Jang-Bom Chai: Dynamics analysis of a pantograph-catenary system using absolute nodal coordinates // Vehicle System Dynamics, 2006, vol.44, 8, pp.615-630.

6. Weihua Zhang, Yi Liu, Guiming Mei: Evaluation of the coupled dynamic response of a pantograph-catenary system: contact force and stresses // Vehicle System Dynamics, 2006, vol.44, 8, pp.645-658.

7. Benet J., Alberto A., Arias E., Rojo T.: A Mathematical Model of the Pantograph-Catenary Interaction with Several Contact Wires // IAENG International Journal of Applied Mathematics, 37:2, 2007.

8. Rauter F., Pombo J., Ambrosio J., Chalansonnet J., Bobilott A., Pereira H.: Contact Model for the Pantograph-Catenary Interaction // Journal of System Design and Dynamics, Vol. 1. No. 3. 2007, pp. 447-457.

9. Rauter F., Pombo J., Ambrosio J., Pereira H.: Multibody Modelling of Pantographs for Pantograph-Catenary interaction. Multiscale Problems in Multibody Sysytem Contacts, 2007, pp.205-226.

10. Arias E., Alberto A., Montesinos J., Rojo T., Cuartero F., Benet J.: A mathematical model of the static pantograph/catenary interaction // Int. J. of Comp. Math., 2009, vol. 86, 2.

11. Галкин А.Г. и др.: Математическое моделирование взаимодействия контактной подвески КС-200-25 и токоприемника. Отчет УрГУПС, 2007.

12. Веселов В.В.: Совершенствование расчетов динамического взаимодействия контактной сети и токоприемников на основе метода конечных элементов. Автореферат канд. дисс., Екатеринбург, 2000.

13. Голубков А.С.: Совершенствование методов и аппаратных средств определения рациональных параметров скоростных контактных подвесок. Автореферат канд. дисс., Омск, 2009.

14. Dahlberg T. Moving Force On Loaded Beam – With Applications To A Railway Overhead Contact Wire // Vehicle System Dynamics. – Aug.2006. - No.8. – с. 631-644.

15. Kiessling F., Puschmann R., Schmieder A. Contact Lines for Electrical Railways. Germany: SIEMENS, 2009. – 994 с

16. Технический отчет. «Моделирование контактной подвески методом конечных элементов в статике. Трехмерная задача». ЗАО «Универсал – контактные сети», Санкт–Петербургский государственный политехнический университет (кафедра «Прикладная математика»). Санкт-Петербург. 2010.

17. Zienkiewicz O.C., Taylor R.L. The Finite Element Method. Volume 1: The basis. 2000. 689 p.

18. Christoph L.,and Simeon B. Solving constrained mechanical systems by the family of Newmark and α-methods // ZAMM. Z. Angew. Math. Mech. 86, No. 10, 772 – 784 (2006).

19. Newmark, N. A method of computation for structural dynamics // ASCE J. Eng. Mech. Div. 85, 67–94, 1959.

20. Negrut D., Khude N., and Heyn T. A discussion of low order numerical integration formulas for rigid and flexible multibody dynamics. http://sbel.wisc.edu/documents/IntegratorReport.pdf.

21. Chung, J., Hulbert, G., A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method // ASME Journal of Applied Mechanics 60, 371–375 (1993).

22. Hilber H., Hughes T., and Taylor R. Improved numerical dissipation for time integration algorithms in structural dynamics // Earthqu. Eng. Struct. Dyn. 5, 283–292 (1977).

23. Wood, W. L., Bossak, M., and Zienkiewicz, O. C. An Alpha Modification of Newmark’s Method // International Journal for Numerical Methods in Engineering, Vol. 15, pp. 1562-1566. 1981.

24. Теребиж В. Ю. Анализ временных рядов в астрофизике. - М., Наука. 1992. 392 с.