11 Вариант. Решение Для представленной на рисунке 1 цепи эквивалентная передаточная функция (ПФ) будет иметь вид Запишем пф с учётом числовых коэффициентов и сведём пф к стандартному виду
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное агенство морской и речной транспорта ФГБОУ «Сибирский государственный университет водного траспорта» Якутский институт водного транспорта (филиал) Курсовая работа по дисциплине: «Теория Автоматического управления» Работу выполнил Студент 2 курса Группа - ЭЭ-19-2 Очного отделения Иванов В.В. Научный руководитель Петров.П.П Якутск 2023 ЗАДАНИЕ 2. Построить амплитудно-фазовую характеристику звена, изображенного на рис. 1.2, в соответствии с вариантом. Исходные данные приведены в таблице 2.1. Таблица 2.1 - Исходные данные к заданию 2
 Рисунок 2.1 - Исходная схема. Решение Для представленной на рисунке 2.1 цепи эквивалентная передаточная функция (ПФ) будет иметь вид:  Запишем ПФ с учётом числовых коэффициентов и сведём ПФ к стандартному виду:
W(p)=20+1,5*20*p/20+p*(1,5*20+20)=0,95p Получили вещественную частотную характеристику: Uω=-ωTKω3T2+ω=-8ω0.04ω3+ω и мнимую частотную характеристику: Vω=-Kω3T2+ω=-400.04ω3+ω Амплитудно-фазовая частотная характеристика (АФЧХ) представляет собой годограф вектора W(jω) при изменении частоты ω от 0 до ∞ . АФЧХ может быть построена в декартовой системе координат, в которой по оси абсцисс откладываются значения P(ω), а по оси ординат – Q(ω) . АФЧХ может быть построена в декартовой системе координат, в которой по оси абсцисс откладываются значения P(ω), а по оси ординат – Q(ω) Задаваясь различными значениями щ, находим соответствующие им Р (щ) и Q (щ) и их значения оформляем таблично: при щ = 0 Р (щ) = 0,1 и Q (щ) = 0 щ = 0,5 Р (щ) = 0,13 и Q (щ) = 0 щ = 1,0 Р (щ) = ? и Q (щ) = 0 щ = 2,0 Р (щ) = - 0,03 и Q (щ) = 0 щ = 3,0 Р (щ) = -0,0125 и Q (щ) = 0 щ = 5,0 Р (щ) = - 4,17 · 10-3 и Q (щ) = 0 щ = 10,0 Р (щ) = -1 · 10-3 и Q (щ) = 0 Таблица 2 - Расчет амплитудно-фазовой характеристики
По значениям Р (щ) и Q (щ) построить амплитудно-фазовую характеристику не представляется возможным, т.к. фазовая характеристика равна нулю. Для апериодического звена второго порядка амплитудная характеристика имеет вид: К(щ) = к / v(1 - Т22 ·щ 2 )2 = 0,1 / 1 - щ 2 Результаты вычислений выносим в таблицу. Таблица 3- Расчет амплитудной характеристики
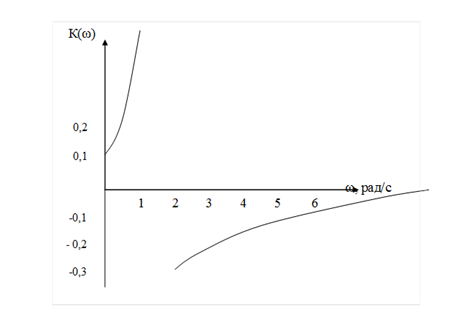 ЗАДАНИЕ №3. Построить логарифмическую амплитудную L() и фазовую () характеристики звена (таблица 3.1), выбранного в соответствии с вариантом. Таблица 3.1
Решение Передаточная функция звена с учётом числовых коэффициентов: Передаточная функция инерционного звена равна 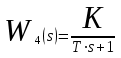 . .Комплексный коэффициент передачи звена будет:  Для нахождения вещественной и мнимой частотных характеристик инерционного звена представим это выражение в следующем виде:  отсюда получим вещественную и мнимую частотные характеристики инерционного звена отсюда получим вещественную и мнимую частотные характеристики инерционного звена 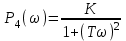 , , 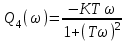 . Из полученных зависимостей следует, что функция . Из полученных зависимостей следует, что функция  - четная, а функция - четная, а функция  - нечетная. - нечетная.Для нахождения годографа АФЧХ инерционного звена, зависимости Q4() от P4(), найдем уравнение в функции от переменных  и и  . .Получим 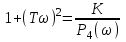 . Подставляя это выражение в формулу для Q4(), находим: . Подставляя это выражение в формулу для Q4(), находим: 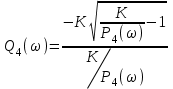 . Преобразуя эту зависимость, имеем: . Преобразуя эту зависимость, имеем: 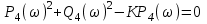 . Таким образом, годограф амплитудно-фазовой частотной характеристики (АФЧХ) инерционного звена представляет собой окружность . Таким образом, годограф амплитудно-фазовой частотной характеристики (АФЧХ) инерционного звена представляет собой окружностьУчитывая известную связь между частотными характеристиками найдем амплитудно-частотную и фазовую частотные характеристики:  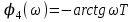 . .Действительная логарифмическая амплитудная частотная характеристика равна 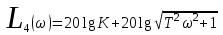 Характеристика  имеет низкочастотную имеет низкочастотную 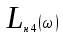 и высокочастотную и высокочастотную  асимптоты, которые сопрягаются на частоте сопряжения асимптоты, которые сопрягаются на частоте сопряжения 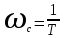 . .Низкочастотная асимптота ЛАЧХ инерционного звена представляет собой предел, при этом  и второе слагаемое ЛАЧХ равно нулю. и второе слагаемое ЛАЧХ равно нулю. Высокочастотная асимптота ЛАЧХ находится как из условия 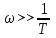 . Тогда . Тогда  и и 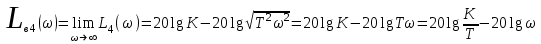 . .Асимптотической ЛАЧХ является характеристика, составленная из асимптот - двух прямых линий: 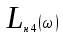 и и   Графики  и показаны на рис. 5.7. и показаны на рис. 5.7.Эти характеристики имеют следующие особенности: низкочастотная асимптота  имеет 0 наклон, имеет 0 наклон,высокочастотная асимптота  имеет наклон–20 дБ/дек, имеет наклон–20 дБ/дек,асимптоты и сопрягаются на частоте сопряжения 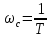 . .фазочастотная характеристика на частоте сопряжения 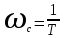 принимает значение принимает значение  при уменьшении частоты относительно частоты сопряжения 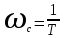 фазочастотная характеристика стремиться к нулю; фазочастотная характеристика стремиться к нулю;при увеличении частоты относительно частоты сопряжения 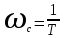 фазочастотная характеристика стремиться к значению фазочастотная характеристика стремиться к значению  . . рис. 5.7. Асимптотическая логарифмическая амплитудная частотная характеристика инерционного звена   Рисунок 3.1 - ЛАЧХ ЛФЧХ - это ФЧХ в логарифмическом масштабе по оси абсцисс:  L( L( ), дБ ), дБ20 20lgk -20дБ\дек Рисунок 3.2 - ЛФЧХ Примечание. Множитель 180/π введён для перевода величин ЛФЧХ из радиан в градусы. ЗАДАНИЕ №4. Построить амплитудно-фазовую характеристику для системы, изображенной на рис. 4.1 – 4.10. Исходные данные в соответствии с вариантами приведены в таблицах 4.1, 4.2. Таблица 4.1
 Таблица 4.2
Решение [Примечание. В таблице 4.1 указана ПФ звена W6(p), однако в таблице 4.2 числовые коэффициенты k6 и Т6 не заданы. Поскольку числовые коэффициенты не заданы, полагаем, что данное звено отсутствует] Эквивалентная передаточная функция (ПФ) системы11 варианта: Wjω=Kjω1+jωT=K-ω2T+jω=K-ω2T-jωω4T2+ω2=-ω2TKω4T2+ω2+ +j-ωKω4T2+ω2=-ωTKω3T2+ω+j-Kω3T2+ω Получили вещественную частотную характеристику: Uω=-ωTKω3T2+ω=-8ω0.04ω3+ω и мнимую частотную характеристику: Vω=-Kω3T2+ω=-400.04ω3+ω Амплитудно-фазовая частотная характеристика (АФЧХ) представляет собой годограф вектора W(jω) при изменении частоты ω от 0 до ∞ . АФЧХ может быть построена в декартовой системе координат, в которой по оси абсцисс откладываются значения P(ω), а по оси ординат – Q(ω) . АФЧХ может быть построена в декартовой системе координат, в которой по оси абсцисс откладываются значения P(ω), а по оси ординат – Q(ω) Откладывая по оси абсцисс действительную составляющую, а по оси ординат мнимую составляющую, строим АФХ при изменении частоты ω от 0 до ∞: 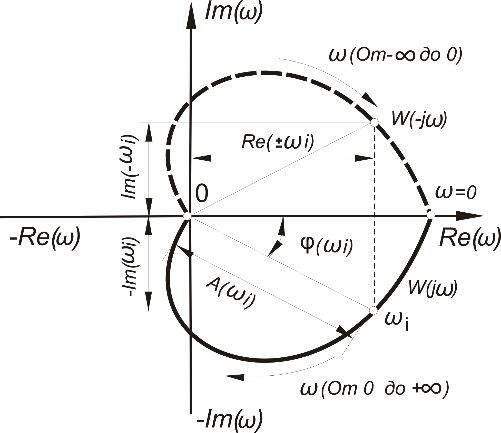 Рисунок 4.1 - Годограф АФХ ЗАДАНИЕ 5. Построить логарифмические амплитудную и фазовую частотные характеристики для системы, изображенной на рис. 4.1 – 4.10. Исходные данные в соответствии с вариантами приведены в таблицах 4.1, 4.2. Решение В ходе выполнения задания 4 была определена ПФ системы и выведены выражения
Запишем комплексный коэффициент передачи формальной заменой s на jω в передаточной функции разомкнутой системы и выведем полученное выражение на экран с помощью «символьной стрелки», вызываемой также из палитры Символьные операторы: 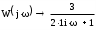 Для нахождения вещественной 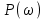 и мнимой и мнимой 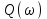 частотных характеристик звена воспользуемся стандартными функциями Mathcad: Re() и Im() соответственно: частотных характеристик звена воспользуемся стандартными функциями Mathcad: Re() и Im() соответственно: , ,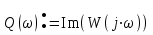 Для нахождения вещественной и мнимой частей выражения в Mathcad имеются специализированные встроенные функции:  Выбрать из командной строки опцию «вставка функции» f(x) и из предложенного списка слева – категория функции – комплексные числа (Complex Number), из предложенного списка справа – имя функции Re() или Im() – далее клик по кнопке «ОК» или «добавить». 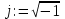 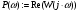  Однако возможности Mathcad не позволяют сразу получить комплексный коэффициент передачи в виде суммы вещественной и мнимой частей. При этом следует учесть, что комплексный коэффициент передачи может быть представлен в виде  , ,где  - вещественная часть комплексного коэффициента передачи, - вещественная часть комплексного коэффициента передачи, - мнимая часть комплексного коэффициента передачи. - мнимая часть комплексного коэффициента передачи. Тогда мнимая и вещественная части будут равны:  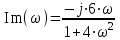 Для построения годографа АФЧХ звена зададим диапазон и шаг изменения аргумента (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»: 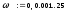 Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем P(ω), а на оси ординат – Q(ω): Для построения вещественной 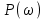 и мнимой и мнимой 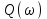 частотных характеристик звена зададим диапазон и шаг изменения аргумента (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»: частотных характеристик звена зададим диапазон и шаг изменения аргумента (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»: : =0, 0.1 .. 1000 Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем , а на оси ординат –P(ω) или Q(ω): Теперь определим амплитудную-частотную (АЧХ) и фазовую частотную (ФЧХ) характеристики. По определению, АЧХ вычисляется как модуль комплексного коэффициента передачи, а ФЧХ - как его аргумент:    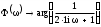 Действительная логарифмическая АЧХ в соответствии с определением вычисляется по формуле  : :Примечание. Множитель 180/π введён для перевода величин ЛФЧХ из радиан в градусы. ЗАДАНИЕ 6. Определить устойчивость автоматической системы с помощью алгебраического критерия, характеристическое уравнение которой имеет вид, приведенный в таблице 6.1. Таблица 6.1
Решение Оцениваем устойчивость системы алгебраическим критерием Гурвица. Характеристическое уравнение системы: 2р6 + 3р5 +3р4 + 5р3 + 7р2 + 7р + 200 = 0 По необходимому условию Гурвица, все коэффициенты характеристического уравнения должны быть положительными. Необходимое условие устойчивости выполняется. По достаточному условию устойчивости, все определители матрицы Гурвица должны быть положительными. Формируем матрицу Гурвица: Из коэффициентов характеристического уравнения замкнутой системы a0рn + a1рn-1 + … + an = 0 составляется таблица, называемая матрицей Гурвица по следующему правилу: 1) по диагонали сверху вниз записываются все коэффициенты, начиная с a1 до an в порядке возрастания индексов; 2) столбцы дополняются вверх коэффициентами с возрастающими индексами, вниз коэффициентами с убывающими индексами; 3) на месте коэффициентов с индексами больше n и меньше нуля проставляются нули. Матрица Гурвица:  Рассчитываем определители матрицы Гурвица:  Определители 5 и 6 порядка матрицы Гурвица отрицательные, следовательно, система неустойчива. ЗАДАНИЕ №7. Определить устойчивость системы автоматического управления по критерию Михайлова в соответствии с заданием, приведенным в таблице 7.1. Таблица 7.1
Решение Заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j: D(jw) = 2(jw)3 + 9(jw)2 + +13(jw) + 6 = –2jw3 – 9w2 + +13jw + 6 = (6 – 9w2) + j(13w – 2w3). Выделяем действительную и мнимую части: Re(w) = 6–9w2; Im(w) =13w – 2w3. Задаваясь значениями частоты из интервала [0; ¥), строим годограф Михайлова (рис. 5): 1) w = 0, Re = 6, Im = 0 – годограф начинается на положительной части действительной оси Re; 2) Re = 0 Þ 6 – 9×w2 =0 Þ 3) 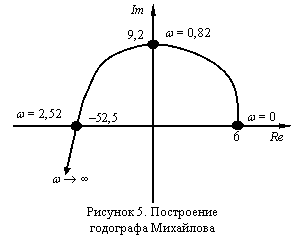 Im = 0 Þ 13×w – 2×w3 = 0; w×(13–2w2) = 0; w1 = 0; Вывод. Все условия критерия Михайлова соблюдены, система устойчива. ЗАДАНИЕ №8. Определить устойчивость электромеханической системы, используя критерий Найквиста. Передаточная функция разомкнутой системы в соответствии с вариантом приведена в таблице 7.1. Решение Передаточная функция колебательного звена: Передаточная функция для единичного ступенчатого воздействия Выполним обратное преобразование Лапласа (см. табл. 3, прил. 1) и получим переходной процесс для единичного ступенчатого воздействия:  . .Строим график переходного процесса при T = 25, x = 0,5,k = 8 (рис. 10)  Рисунок 10. Переходной процесс колебательного звена при T = 25, x = 0,5, k = 8 Из графика следует, что объект нейтрален. 2. Оценка устойчивости по алгебраическим критериям. Корневой критерий Ляпунова Характеристическое уравнение для передаточной функции колебательного звена: Критерий Рауса-Гурвица Так как все коэффициенты характеристического уравнения положительны, то необходимое условие устойчивости объекта выполнено. Для проверки достаточного условия составим определители характеристического уравнения: Так как все определители, составленные из коэффициентов характеристического уравнения, положительны, объект является устойчивым. 3. Оценка устойчивости по частотным критериям. Критерий Михайлова В характеристическом полиноме D(p)=252·p2+2·0,5·25·p+1, заменяем р на jw, избавляемся от старших степеней j и группируем слагаемые, содержащие и не содержащие j: D(jw) = 625(jw)2 + 25(jw) + 1 = – 625w2 + 25jw + 1 == (1 – 625w2) + j×25w.  Рисунок 11. Годограф Михайлова для Выделяем действительную и мнимую части: Re = 1 – 625w2; Im = 25w. Задаваясь значениями частоты из интервала [0; ¥[, строим годограф Михайлова (см. рис. 11). Вывод. Годограф Михайлова при изменении частоты от 0 до ¥ начинается на положительной части действительной оси комплексной плоскости при w = 0 Re = 1, Im = 0, проходит последовательно против часовой стрелки n квандрантов плоскости, нигде не обращается в 0 и не проходит через начало координат (n = 2 – порядок характеристического уравнения системы). Следовательно, объект устойчив. Критерий Найквиста Для разомкнутой системы  , ,откуда Задаваясь значениями частоты из интервала [0; ¥[, строим АФЧХ колебательного звена (см. рис. 12). Вывод. Разомкнутая система устойчива, а так как амплитудно-фазовая частотная характеристика разомкнутой системы не охватывает на комплексной плоскости точку с координатами (–1; j0), следовательно замкнутая система будет тоже устойчива. ЗАДАНИЕ 9. Определить устойчивость замкнутой системы по логарифмическим характеристикам разомкнутой системы. В случае устойчивости определить запасы устойчивости по амплитуде и фазе. Исходные данные для вариантов приведены в таблице 9.1. Таблица 9.1
Решение По логарифмическому критерию, замкнутая система устойчива, если на частоте среза ЛАЧХ разомкнутой системы (частоте, на которой ЛАЧХ пересекает ось абсцисс) значение ЛФЧХ составляет: φ(ω) > -180º. Запишем ПФ системы с учётом числовых коэффициентов: 330/p*(0,23*p+1)*(0,08*p+1) Запишем выражения амплитудно-частотной характеристики (АЧХ) А(ω) и фазовой частотной характеристики (ФЧХ) звена φ(ω) как произведение и сумму АЧХ и ФЧХ типовых звеньев САУ соответственно: Зная, что ЛАЧХ - это АЧХ в логарифмическом масштабе А ЛФЧХ - это ФЧХ в логарифмическом масштабе только по оси абсцисс, строим ЛАЧХ и ЛФЧХ:  Рисунок 9.1 - ЛАЧХ и ЛФЧХ разомкнутой системы На частоте среза ЛАЧХ разомкнутой системы значение ЛФЧХ составляет: φ(ωср) = -239º < -180º, следовательно, замкнутая система неустойчива. Запасы устойчивости отсутствуют. |

 .
. .
.