методичка тпр. 1. Некритериальные задачи принятия решений 6

• Название: 1. Некритериальные задачи принятия решений 6
• Анкор: методичка тпр
• Дата: 19.01.2022
• Размер: 0.92 Mb.
• Имя файла: 0_Metodicheskie_ukazania_po_vypolneniyu_raschetno-graficheskikh_.doc
• Тип: Реферат; #336524
• страница: 1 из 4

Содержание

Введение 4

1.Некритериальные задачи принятия решений 6

1.1.Расчетно-графическая работа № 1. Некритериальные методы принятия решений 6

2.Многокритериальные задачи принятия решений 14

2.1.Расчетно-графическая работа № 2. Метод БОФа 14

2.2.Расчетно-графическая работа № 3. Метод анализа иерархий Саати 22

3. Принятие решений в условиях неопределенности 33

3.1.Расчетно-графическая работа № 4. Критерии Вальда, Байеса-Лапласа, Сэвиджа и Гурвица 33

Список литературы 39

Введение

Все задачи принятия решений (ЗПР) по способу структурирования альтернатив можно разделить на две группы – критериальные и некритериальные. В первой группе структурирование альтернатив основано на их сопоставлении по некоторому набору критериев. Например, необходимо выбрать лучший инвестиционный проект, исходя из критериев – объем инвестиций, срок окупаемости, риск потери инвестиций. В некритериальныхметодах альтернативы сравниваются «в целом». При этом используется способность человеческого мозга создавать общее представление (мнение) о предмете. В психологии и кибернетике такое общее представление обозначают термином «гештальт». Это целостный образ объекта, лишенный какой бы то ни было детализации. Примером некритериального структурирования является ранжирование альтернатив.

Целью расчетно-графической работы № 1 является изучение двух некритериальных методов – метода Борда и метода поиска медианы Кемени.

Целью расчетно-графических работ № 2 – 3 является изучение методов решения многокритериальных ЗПР, в том числе получение навыков выбора того или иного метода в зависимости от имеющейся исходной информации. Рассматриваются метод БОФа и метод анализа иерархий Саати.

Если информация об объектах представлена в виде значений набора критериев, то в качестве моделей можно предложить метод БОФа и метод анализа иерархий Саати. Метод БОФа позволяет решать задачу выбора, если критерии являются количественными или измеряются в порядковой шкале. Метод анализа иерархий Саати может применяться в тех случаях, когда эксперты не могут дать абсолютные оценки альтернатив по критериям, а пользуются более слабыми сравнительными измерениями (парными сравнениями), что на практике случается достаточно часто.

Задача принятия решений в условиях неопределенности – это задача выбора оптимальной стратегии (решения), исход которой помимо стратегий оперирующей стороны и ряда факторов (детерминированных и стохастических) зависит от неопределенных факторов, неподвластных оперирующей стороне и неизвестных ей в момент принятия решений.

Вследствие влияния неопределенных факторов каждой конкретной стратегии (решению) соответствует не единственный исход, а множество исходов. Конкретная реализация исхода для каждого решения определяется конкретной реализацией неопределенных факторов.

Учет неопределенных факторы, закон распределения которых неизвестен, базируется на формировании специальных критериев, на основе которых принимаются решения – критерии Вальда, Сэвиджа, Гурвица и Байеса-Лапласа.

Целью лабораторной работы № 4 является изучение критериев Вальда, Сэвиджа, Гурвица и Байеса-Лапласа, а также условий их применения.

1. Некритериальные задачи принятия решений

1. Расчетно-графическая работа № 1. Некритериальные методы принятия решений

1. Цель работы

Целью работы является изучение некритериальных методов принятия решений – метода Борда и метода поиска медианы Кемени.

2. Постановка задачи

Дано:

• 
  a₁,a₂, …, a_n – альтернативы, n – количество альтернатив,
  
• 
  P₁, P₂, … P_m – индивидуальные ранжирования альтернатив экспертами, m – количество экспертов.
  

Ранжирования имеют вид 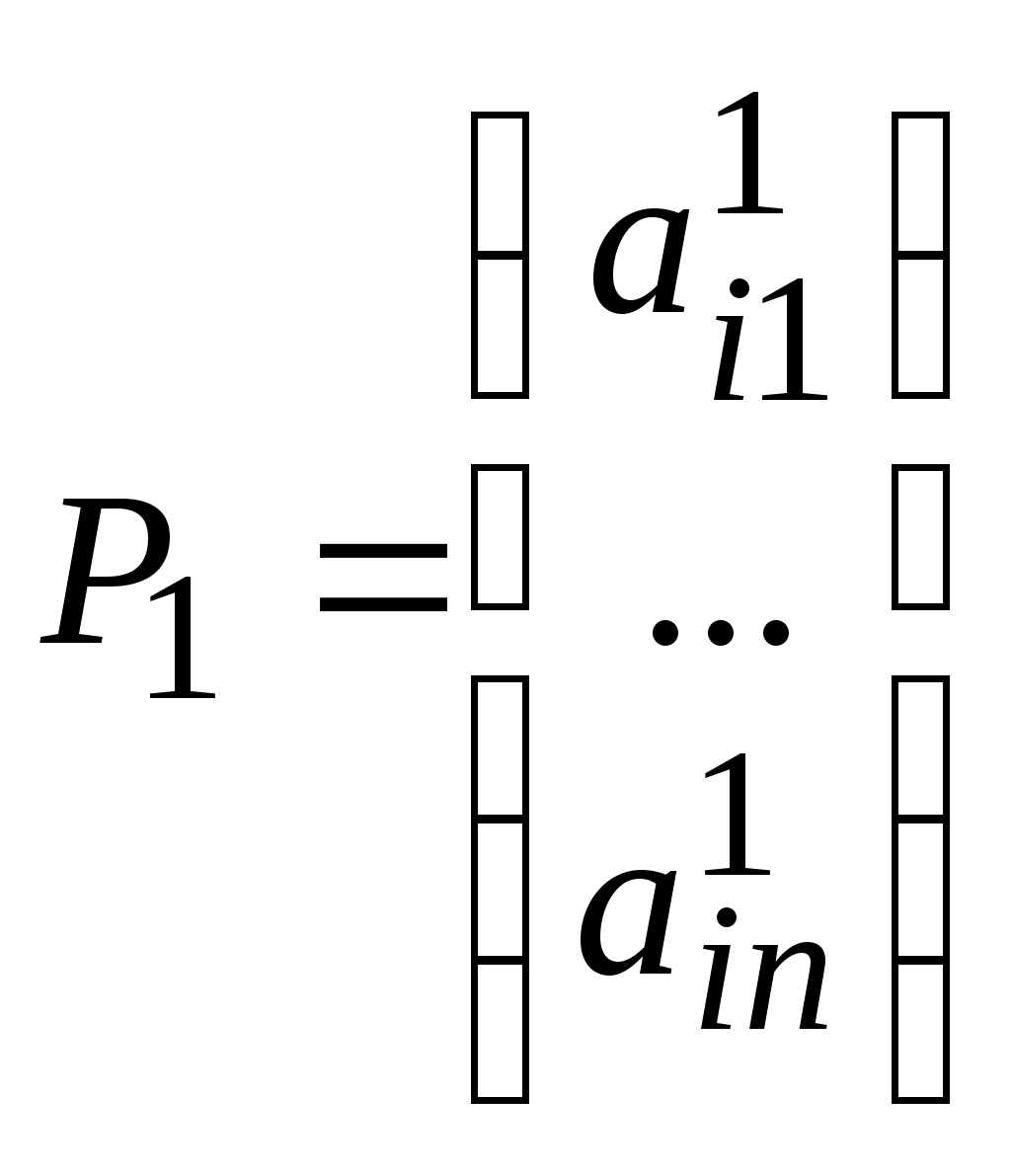, где – альтернатива, стоящая на первом месте в ранжировании P₁, – альтернатива, стоящая на n-ом месте в ранжировании P₁. Альтернатива имеет ранг 1, альтернатива имеет ранг n.

Требуется найти: итоговое ранжирование P*, учитывающее мнение всех экспертов с помощью метода Борда и метода поиска медианы Кемени.

3. Метод Борда

В основе метода Борда лежит упорядочивание альтернатив на основе сумм рангов, назначенных альтернативам экспертами [1, с. 62]. Альтернативам, проранжированным экспертами, ставится в соответствие число: последней по предпочтению – 0, предпоследней – 1 и т.д. Метод состоит из 2 этапов:

1. 
   на первом этапе для каждого объекта с номером k определяется величина S_k, равная сумме рангов, присвоенных объекту всеми экспертами:
   

;

2. 
   на втором этапе определяется ранг объекта – чем больше величина S_k, тем выше место альтернативы в искомом ранжировании.
   

Пример построения итогового ранжирования с помощью метода Борда

Пусть имеются альтернативы a₁,a₂,a₃, a₄ и ранжирования этих альтернатив экспертами (табл. 1). Требуется найти итоговое ранжирование.
Таблица 1

Ранжирования критериев экспертами

P1	a3	P2	a2	P3	a1	P4	a4
	a2		a3,		a3,a4		a3
	a4		a4		a2		a1, a2
	a1		a1

Обозначим полученные на основе ранжирований альтернатив экспертами ранги R₁,R₂,R₃,R₄.Процесс построения итогового ранжирования с помощью метода Борда представлен в табл. 2.

Таблица 2

Построение итогового ранжирования

Альтернатива	R1	R2	R3	R4	Сумма рангов Sk	Место в итоговом ранжировании
a1	0	0	2	0	2	3
a2	2	3	0	0	5	2
a3	3	2	1	1	7	1
a4	1	1	1	2	5	2

4. Метод поиска медианы Кемени

Метод поиска медианы Кемени позволяет найти такое итоговое ранжирование P, суммарное расстояние от которого до всех заданных ранжирований минимальное:

,

где m – количество экспертов, P₁, …, P_m – ранжирования, d(P,P_) – расстояние между ранжированиями [1, с. 73].

Таким образом, для поиска медианы необходимо ввести понятие расстояния между ранжированиями. Оно определяется с помощью матриц отношений 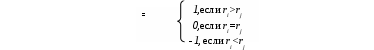, , , n – количество альтернатив.



r_i, r_j – ранги i-той и j-той альтернатив в ранжировании h-ого эксперта. Отметим, что ранги альтернатив сравниваются наоборот, то есть ранг r_i=1>r_j=2 (ранг 1 больше ранга 2) и r_i=5<r_j=3 (ранг 5 меньше ранга 3).

Расстояние от произвольного ранжирования P, которому соответствует матрица , до всех ранжирований P₁, P₂, …, P_m, которым соответствуют матрицы парных отношений , …, определяется по формуле:

.

Для нахождения медианы Кемени вводится матрица потерь , .

,

где P – ранжирование, элемент матрицы отношений p_ij которого равен 1.

При этом задача поиска медианы Кемени для ранжирований формулируется как задача отыскания такого упорядочения альтернатив, а следовательно, строк и столбцов матрицы потерь, чтобы сумма ее элементов, расположенных над диагональю, была минимальна.

Эвристический алгоритм поиска медианы Кемени

Пусть для исходных ранжирований матрица потерь определена. Процесс поиска итогового ранжирования состоит из 2 этапов.

На первом этапе строится предварительное ранжирование P_I.

1-я итерация. Подсчитаем суммы элементов строк матрицы потерь:

.

Найдем минимальную из них .

Альтернативу а_i1, ставим на первое место в искомом ранжировании. Вычеркивая в строку и столбец с номером i₁, получаем матрицу , множество индексов строк и столбцов которой соответственно I⁽¹⁾=J⁽¹⁾={1,…,n}\ I₁.

k-я итерация. В матрице потерь подсчитаем суммы элементов строк:

.

Найдем минимальную из них: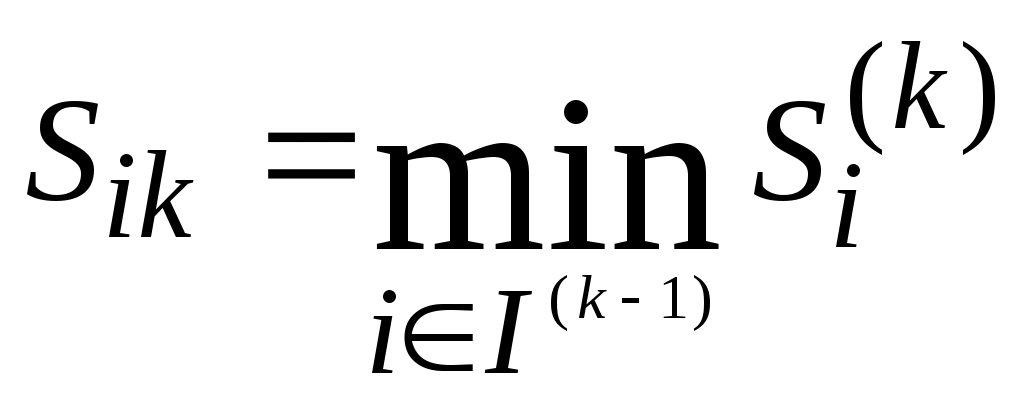

.

Альтернативу а_ik, ставим на k-тое место в искомом упорядочении. Вычеркивая в строку и столбец с номером i_k, получаем матрицу , множество индексов строк и столбцов которой соответственно I^(k)=J^(k)={1,…,n}\ {i₁, …,i_k}.

Алгоритм завершается после n-й итерации (I^(k)=J^(k) и равны пустому множеству). Искомое упорядочение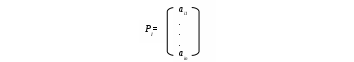



На втором этапе из найденного ранжирования P_I получают итоговое ранжирование P_II, при этом процесс перехода от ранжирования P_I к ранжированию P_II происходит следующим образом: для элементов ранжирования P_I последовательно проверяем справедливость соотношений (1)

(1)

Как только для некоторого kоно нарушено, альтернативы a_ik и a_ik+1 в ранжировании меняем местами, а соотношение (1) проверяем, начиная с альтернативы, непосредственно предшествующей альтернативе, подвергшейся перестановке. После конечного числа шагов будет получено ранжирование P_II.

Пример построения итогового ранжирования с помощью метода поиска медианы Кемени

Рассмотрим процесс построения итогового ранжирования на примере, рассмотренном ранее (исходные данные представлены в табл. 1).

1. 
   Построим матрицы отношений для ранжирований экспертов:
   

	0	-1	-1	-1		0	-1	-1	-1
	1	0	-1	1		1	0	1	1
	1	1	0	1		1	-1	0	1
	1	-1	-1	0		1	-1	-1	0
	0	1	1	1		0	0	-1	-1
	-1	0	-1	-1		0	0	-1	-1
	-1	1	0	0		1	1	0	-1
	-1	1	0	0		1	1	1	0

Например, p₁₂⁽¹⁾=-1, так как r₁<r₂ (r₁=3, r₂=1), p₃₄⁽²⁾=0, так как r₃=r₄ (r₃=2, r₄=2).

2. 
   Матрица потерь имеет следующий вид:
   

0	5	6	6
3	0	6	4
2	2	0	3
2	4	5	0

Например, r₁₂=d₁₂(P₁,P₃)+d₁₂(P₂,P₃)+d₁₂(P₄,P₃), так как P₃ – ранжирование, элемент матрицы отношений которого p₁₂⁽³⁾=1.

Тогда r₁₂=|p₁₂⁽³⁾-p₁₂⁽¹⁾|+|p₁₂⁽²⁾-p₁₂⁽³⁾|+|p₁₂⁽³⁾-p₁₂⁽⁴⁾|=|1-(-1)|+ |1-(-1)|+ |1-0|=5.

3. 
   Найдем предварительное ранжирование P_I (первый этап).
   

1-я итерация. Подсчитаем



Минимум достигается на S₃⁽¹⁾. На первое место в ранжировании P_Iпомещается альтернатива a₃, и она из дальнейших рассмотрений исключается.

2-я итерация. Подсчитаем

Минимум достигается на S₄⁽²⁾. На второе место в ранжировании P_I помещается альтернатива a₄, и она из дальнейших рассмотрений исключается.

3-я итерация. Подсчитаем

Минимум достигается на S₂⁽³⁾. На третье место в ранжировании P_I помещается альтернатива a₂, и она из дальнейших рассмотрений исключается. Таким образом, ранжирование P_I имеет следующий вид: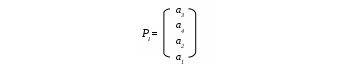

4. 
   Найдем ранжирование Р_II (второй этап).
   

Итак, i₁=3, i₂=4, i₃=2, i₄=1. Сравниваем 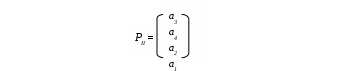и или r₂₁ и r₁₂, Так как r₂₁≤r₁₂ (3≤5), то альтернативы не меняем местами, переходим к сравнению r₄₂ и r₂₄. Так как r₄₂≤r₂₄ (4≤4), то переходим к сравнению r₃₄ и r₄₃. Поскольку r₃₄<r₄₃ (3≤5), то найденное ранжирование



и является ранжированием Р_II, для которого соотношения (1) выполнены.

Итоговые ранжирования альтернатив по методу Борда и методу поиска медианы Кемени представлены в табл. 3.

Таблица 3

Результаты построения итогового ранжирования с помощью метода Борда и метода поиска медианы Кемени

Альтернатива	Место в итоговом ранжировании (Кемени)	Место в итоговом ранжировании (Борд)
a1	4	3
a2	2	4
a3	1	1
a4	3	2

Результаты работы описанных выше методов иногда могут различаться достаточно сильно. Метод Борда дает результаты, которые интуитивно понятны, так как в его основе лежит идея усреднения оценок. Что касается метода поиска медианы Кемени, то он, наоборот, может давать непредвиденные результаты. Для получения итогового ранжирования в методе используется специально оценка – расстояние между ранжированиями. А рассмотренный нами алгоритм получения итогового ранжирования основан на эвристике – предположении, что построенное таким образом итоговое ранжирование и будет наиболее близким к мнению всех экспертов с точки зрения введенной оценки.

5. Варианты заданий

Найти итоговое ранжирование P* с помощью метода Борда и метода поиска медианы Кемени. P₁, P₂, P₃, P₄, P₅ – ранжирования экспертов; a_1, a_2, a_3, a₄ – альтернативы.
Вариант 1

P1	a2	P2	a1	P3	a2, a3	P4	a3
	a4		a3, a4		a4		a2
	a1		a2		a1		a1, a4
	a3

Вариант 2

P1	a4	P2	a3, a4	P3	a1	P4	a2
	a2		a1		a4		a3
	a1		a2		a2, a3		a1, a4
	a3

Вариант 3

P1	a4	P2	a2, a4	P3	a1	P4	a3	P5	a4
	a1		a3		a4		a2		a2
	a2		a1		a2, a3		a1		a1
	a3						a4		a3

Вариант 4

P1	a4	P2	a2, a4	P3	a1	P4	a3	P5	a4
	a1		a3		a4		a2		a2
	a2		a1		a2, a3		a1		a1
	a3						a4		a3

Вариант 5

P1	a4, a3	P2	a2, a4	P3	a1	P4	a3	P5	a4, a3
	a1		a1		a4		a1		a2
	a2		a3		a2		a2		a1
					a3		a4