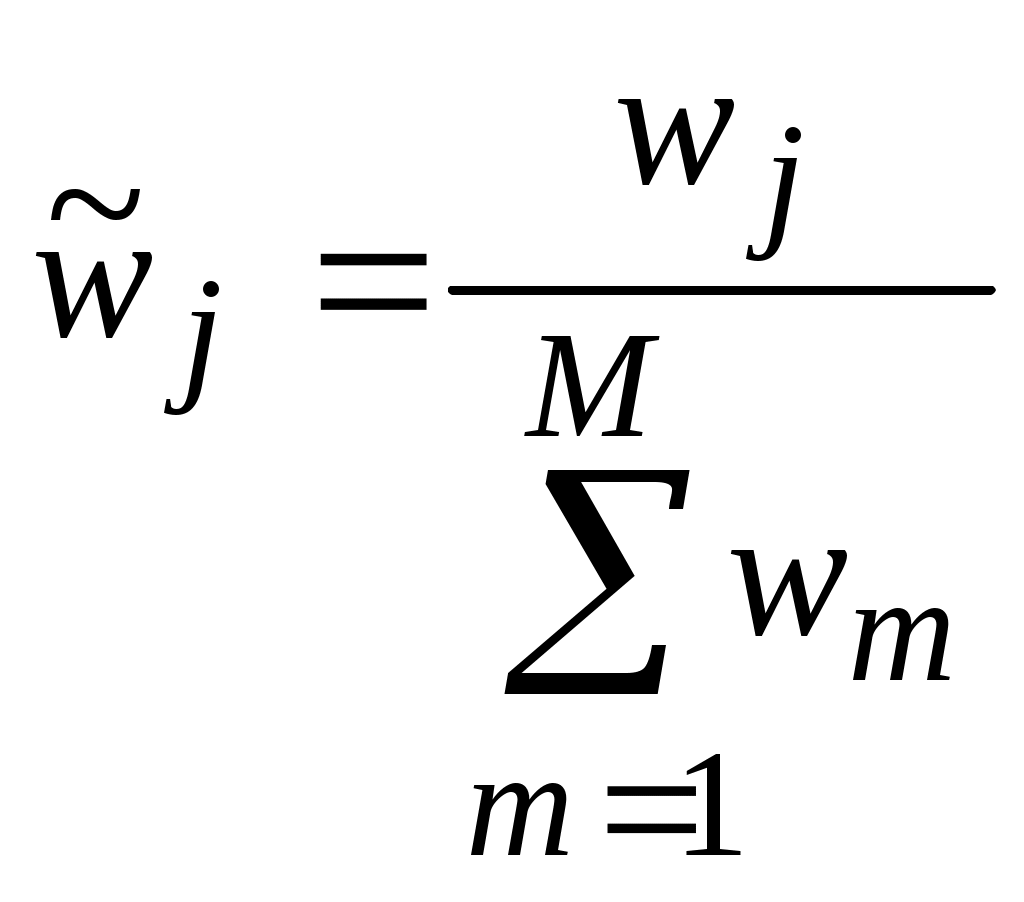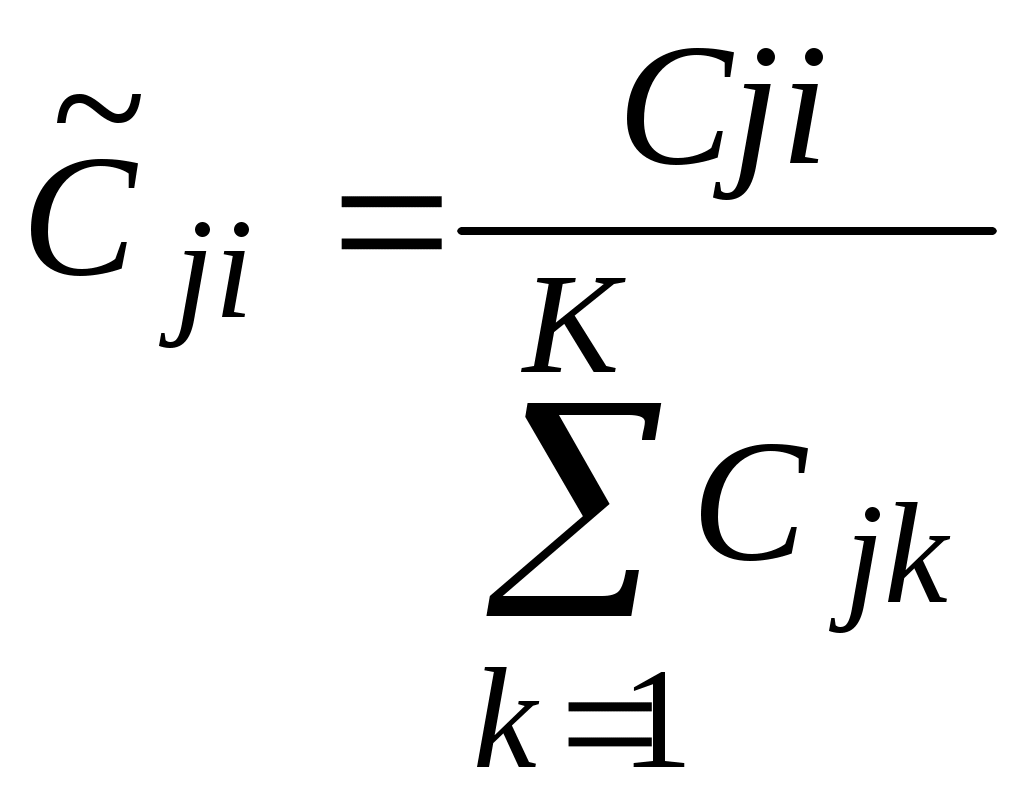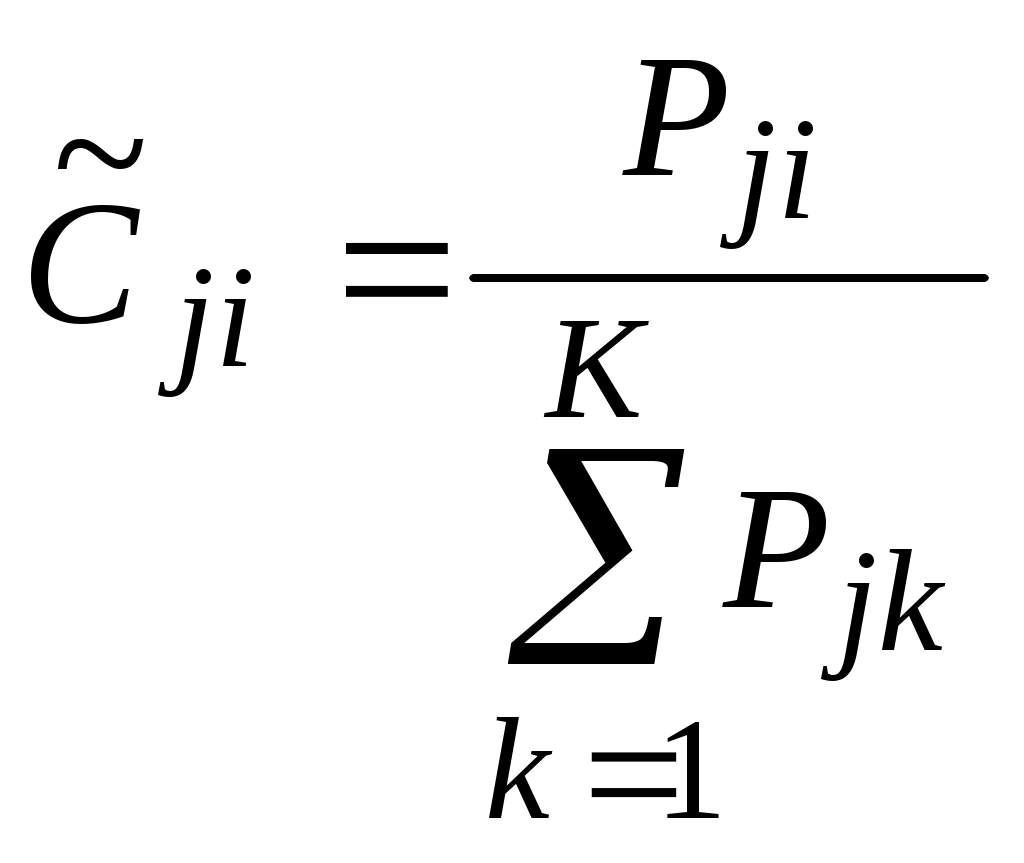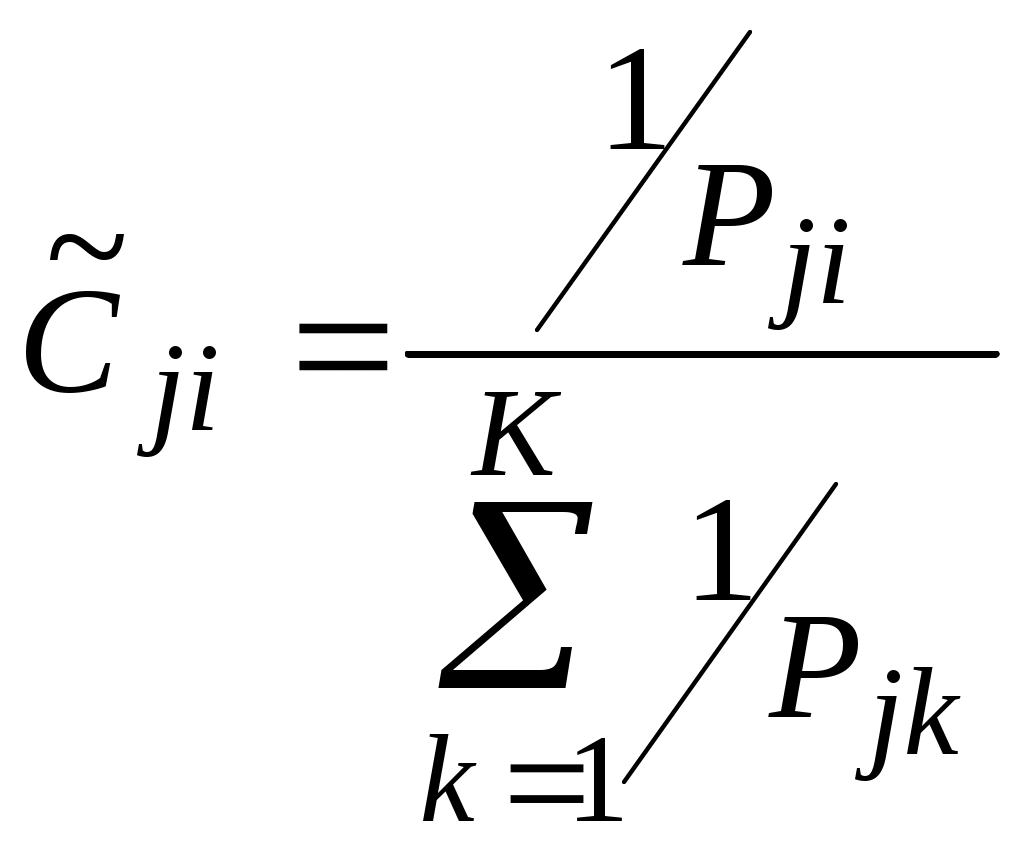методичка тпр. 1. Некритериальные задачи принятия решений 6
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
Многокритериальные задачи принятия решенийЦелью расчетно-графических работ № 2 – 3 является изучение методов решения многокритериальных ЗПР, в том числе получение навыков выбора того или иного метода в зависимости от имеющейся исходной информации. Рассматриваются метод БОФа и метод анализа иерархий Саати. Расчетно-графическая работа № 2. Метод БОФаДанный метод предложен в Быстровым Олегом Филаретовичем для сравнительной оценки инвестиционных проектов по множеству показателей [2, с. 54-63]. Целью метода является определение наиболее приемлемого проекта по заданным показателям. Данный метод может использоваться для оценки любого множества объектов по множеству показателей (критериев). Постановка задачиДано: K – количество объектов, M – количество показателей для сравнения объектов; R=(R1, R2, … RM) – ранжирование показателей по важности; |Cij| – матрица значений показателей для объектов Требуется упорядочить объекты или выбрать лучший объект. Описание алгоритмаМетод БОФа состоит из следующих этапов. Отобрать оптимальное количество показателей. Обозначим показатели Проранжировать показатели по важности в соответствии с предпочтениями ЛПР. Обозначим ранги показателей Определить весовые коэффициенты каждого показателя. Весовые коэффициенты показателей wjопределяются по формуле 1 и затем нормируются по формуле 2:
Проранжировать объекты по важности в соответствии с предпочтениями ЛПР по каждому показателю. Обозначим значения показателей для объектов Pji, ранги объектов по показателям Определить весовые коэффициенты каждого объекта по каждому показателю. Весовые коэффициенты объектов по каждому показателю
Таким образом, для расчета весовых коэффициентов используются отношения порядка между объектами. Однако использование порядковой информации может привести к утрате части полезной информации. При необходимости учета количественной информации весовые коэффициенты показателей рассчитываются по формуле 5, если большие значения показателей предпочтительнее меньших, или по формуле 6, если меньшие значения предпочтительнее больших. При этом этап 4 (ранжирование объектов по каждому показателю) опускается.
Pji – значение показателя j для объекта i.
Рассчитать значения обобщенного показателя для каждого объекта
Проранжировать объекты в соответствии со значениями обобщенных показателей и/или определить лучший объект. ПримерТребуется выбрать лучший инвестиционный проект для реализации. Для сравнения проектов были выбраны показатели: NVP (чистый приведенный доход); IRR (внутренняя норма рентабельности); PI (индекс прибыльности); PP (срок окупаемости); ARR (ср. норма прибыли на инвестиции). Информация о проектах представлена в табл. 4, ранжирование показателей по важности – в табл. 5. Таблица 4
Таблица 5 Ранги показателей
Таким образом, этап 1 и этап 2 уже выполнены. Этап 3. Определение весовых коэффициентов показателей и нормирование их значений. 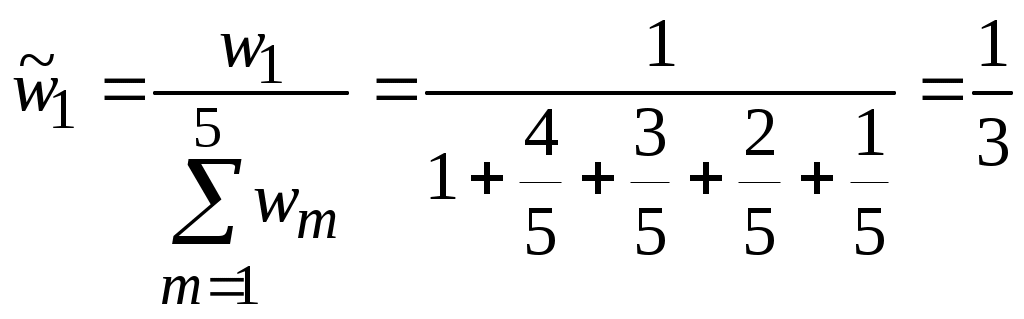 , , Этап 4. Ранжирование объектов по каждому показателю. Проекты сравниваются по каждому показателю и результаты заносятся в табл. 6, Rji – ранг объекта с номером i по показателю с номером j. Таблица 6 Ранги проектов по показателям
Этап 5. Определение весовых коэффициентов объектов по каждому показателю и нормирование полученных значений. Вычислим значения показателя 1 по всем объектам. Пронормируем полученные значения. 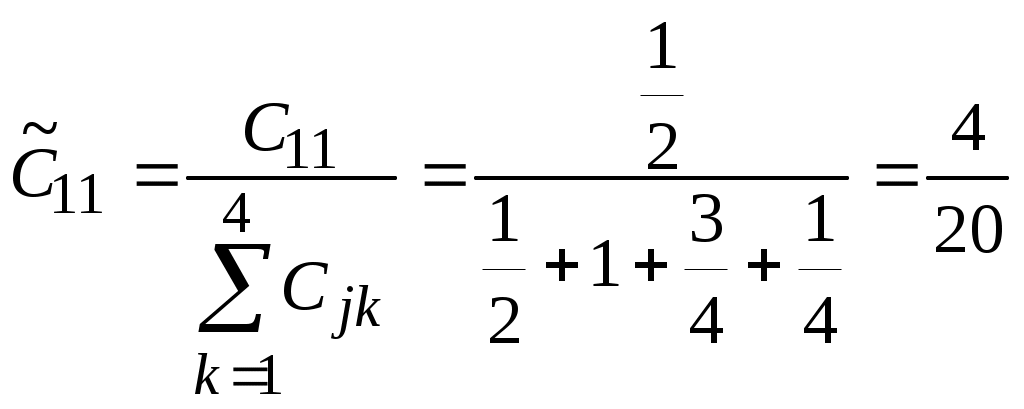 , , 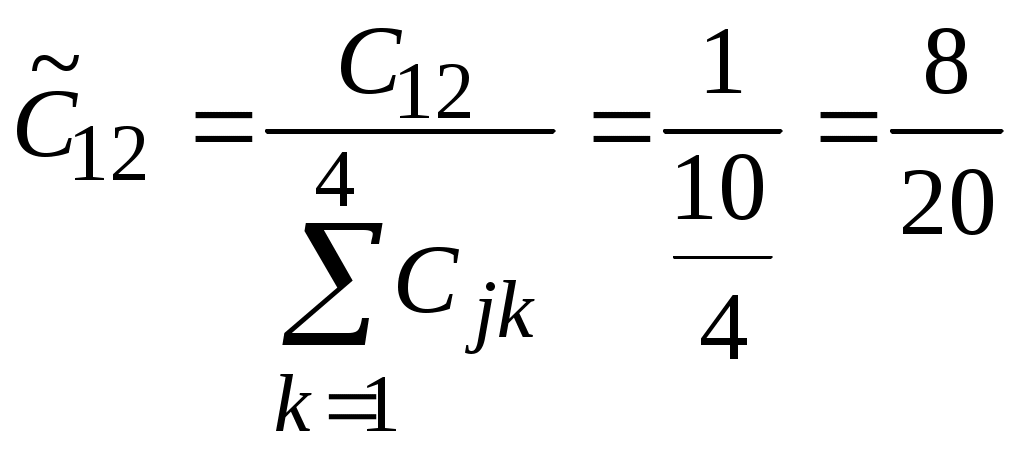 , ,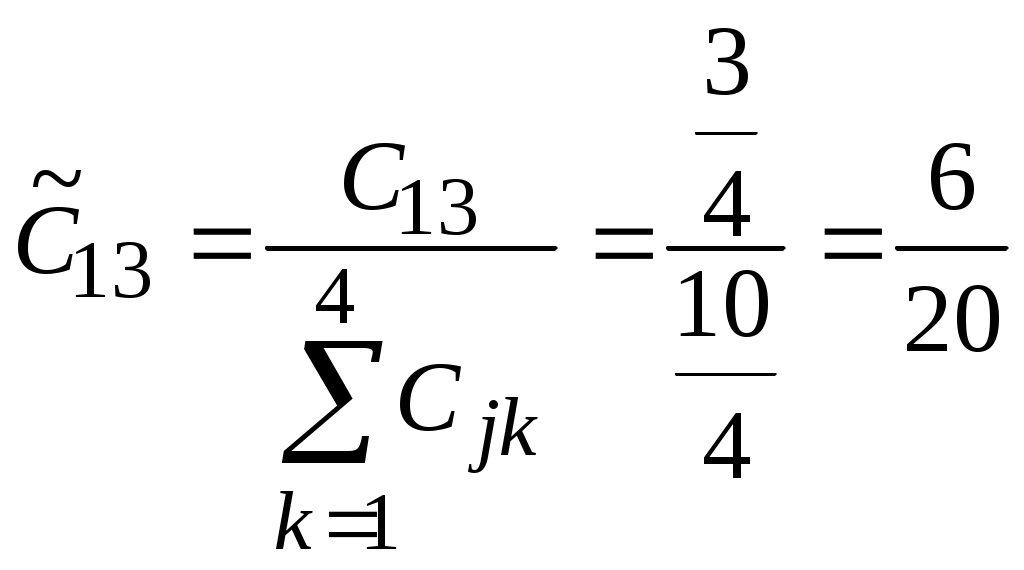 , , 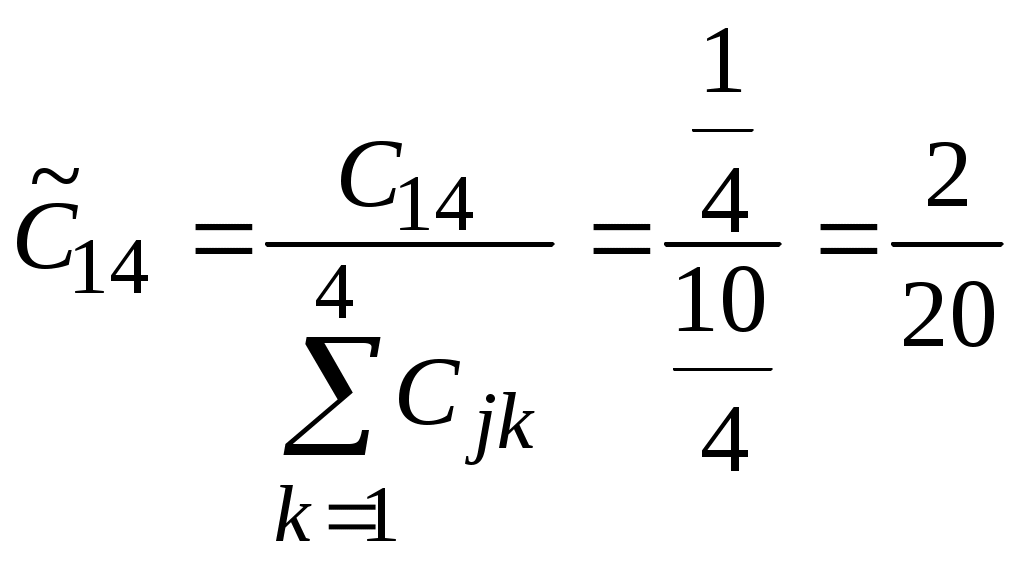 . .Значения остальных весовых коэффициентов объектов по показателям вычисляются аналогично. Этап 6. Расчет значений обобщенного показателя для объектов. 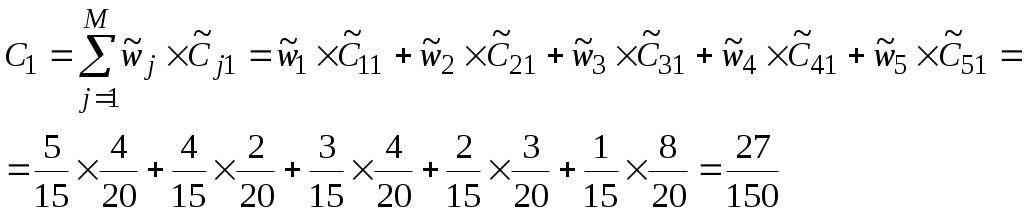 Аналогично вычисляем Этап 7. Таким образом, лучшим является проект 3, на втором месте проект 2, затем идут проекты 3 и 1. Варианты заданийВыбрать лучший инвестиционный проект по методу БОФа. Для сравнения проектов выбраны следующие показатели: W1 – объем инвестиций, млн. дол.; W2 – годовой оборот проекта, млн. дол.; W3 – годовой объем чистой прибыли, млн. дол.; W4 – срок окупаемости проекта, лет; W5 – риск потери инвестиций. При сравнении проектов важно учесть, что для показателей W1, W2, W3 большие значения предпочтительнее меньших, для показателя W4 меньшие значения предпочтительнее больших, а показатель W5 имеет качественную шкалу. Ранжирование показателей по важности представлено в табл. 7, информация о проектах представлена в табл. 8. Таблица 7
Таблица 8
«О» – риск отсутствует, «ОН» – очень низкий риск, «Н» – низкий риск, «В» – высокий риск, «ОВ» – очень высокий риск. Для сравнения проектов по показателю «Риск потери инвестиций» используется порядковая шкала: лучшему значению показателя ставится в соответствие ранг 1, следущему значению ставится в соответствие ранг 2 и т.д. Если несколько проектов имеют одинаковое значение показателя «Риск потери инвестиций», то ранги проектов вычисляются следующим образом. Рассмотрим вариант 1. Проект 1 имеет низкий риск потери инвестиций, проекты 5 и 9 имеют высокий риск потери инвестиций. Тогда проекту 1 в соответствие ставится ранг 1, а проекты 5 и 9 будут иметь одинаковые ранги 2.5, поскольку они разделили 2 и 3 места по этому показателю: Вариант 1 Сравнить инвестиционные проекты с номерами 1, 5 и 9. При сравнении проектов по показателям использовать отношение порядка (формулы 3 и 4). Вариант 2 Сравнить инвестиционные проекты с номерами 1, 5 и 9. При сравнении проектов по показателям использовать количественные соотношения между значениями показателей (формулы 5 или 6, для показателя W5 возможно использование только формул 3 и 4). Вариант 3 Сравнить инвестиционные проекты с номерами 2, 3 и 4. При сравнении проектов по показателям использовать отношение порядка (формулы 3 и 4). Вариант 4 Сравнить инвестиционные проекты с номерами 2, 3 и 4. При сравнении проектов по показателям использовать количественные соотношения между значениями показателей (формулы 5 или 6, для показателя W5 возможно использование только формул 3 и 4). Вариант 5 Сравнить инвестиционные проекты с номерами 5, 6 и 7. При сравнении проектов по показателям использовать отношение порядка (формулы 3 и 4). Вариант 6 Сравнить инвестиционные проекты с номерами 5, 6 и 7. При сравнении проектов по показателям использовать количественные соотношения между значениями показателей (формулы 5 или 6, для показателя W5 возможно использование только формул 3 и 4). Вариант 7 Сравнить инвестиционные проекты с номерами 7, 8 и 9. При сравнении проектов по показателям использовать отношение порядка (формулы 3 и 4). Вариант 8 Сравнить инвестиционные проекты с номерами 7, 8 и 9. При сравнении проектов по показателям использовать количественные соотношения между значениями показателей (формулы 5 или 6, для показателя W5 возможно использование только формул 3 и 4). Вариант 9 Сравнить инвестиционные проекты с номерами 2, 4 и 6. При сравнении проектов по показателям использовать отношение порядка (формулы 3 и 4). Вариант 10 Сравнить инвестиционные проекты с номерами 2, 4 и 6. При сравнении проектов по показателям использовать количественные соотношения между значениями показателей (формулы 5 или 6, для показателя W5 возможно использование только формул 3 и 4). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||