Суждение ( Логика). Вариант 1 Суждение.docx Логика. 1. Образование сложных суждений

• Название: 1. Образование сложных суждений
• Анкор: Суждение ( Логика
• Дата: 23.10.2020
• Размер: 47.2 Kb.
• Имя файла: Вариант 1 Суждение.docx Логика.docx
• Тип: Документы; #145245

Содержание

1. Образование сложных суждений………………………………………………...3

2. Установление логического значения сложных суждений при помощи таблиц истинности…………………………………………………………………………...6

3. Практические задания:…………………………………………………………....8

1. Установите вид следующих сложных суждений и определите их истинность при помощи таблиц истинности:……………………………………...8

1.1. Редакция вправе увеличить или уменьшить размер гонорара.

1.2. Банан – пищевое растение и источник доходов для экспортирующих стран.

1.3. Он сейчас находится в Минске или в Петербурге.

1.4. Кукушка хвалит петуха за то, что хвалит он кукушку.

1.5. Если к двум прибавить два, то получится четыре.

2. Постройте таблицу истинности для следующего выражения:

 (p → (pvq))………………………………………………………………………....10

3. Литература………………………………………………………………………..11

1. Образование сложных суждений.
Суждение – это такая форма мышления, в которой утверждается или отрицается связь между предметом и его признаком или отношение между предметами и которая обладает свойством выражать либо истину, либо ложь.

Суждения бывают простыми и сложными. Простые суждения состоят из двух понятий (терминов суждения) – субъекта и предиката, соединенных между собой логической связкой «есть» («не есть») и имеют структуру S - P. Например, связав понятия «преступление» (S) и «умышленное деяние» (P), можно сформировать простое суждение «Некоторые преступления являются умышленными деяниями». ( Некоторые S есть P)

Рассмотрим структуру сложного суждения на следующем примере.

Два простых суждения:

1) Мошенничество (S) является преступным деянием (P1).

2) Мошенничество (S) преследуется по закону (P2).

С помощью союза «и» могут войти в состав сложного суждения «Мошенничество является преступным деянием и преследуется по закону». С помощью другого союза – «если, ...то» эти простые суждения могут составить другое сложное суждение: «Если мошенничество является преступным деянием, то оно преследуется по закону».

Таким образом, сложное суждение – это суждение, которое состоит из двух и более простых суждений, связанных между собой логическими союзами. Сложные суждения образуются из простых суждений и логических союзов. Союз является важнейшим элементом в структуре сложного суждения. По союзу определяются его вид и логические характеристики. От союза зависят и условия истинности сложного суждения.

В разных логических системах используются различные обозначения логических союзов. Главное заключается в том, что логический союз – не просто значок. Каждый из них выражает определенный вид связи предметов реального мира.

1.1 Таблица основных логических связок

Символический язык		Естественный язык			Смысл союза
1	2		3	4		5
 , ̶ ,	отрицание		отрицание	«не», «неверно, что»		отрицание, сомнение
&, ˄, •	конъюнкция		соединительный	«и», «а», «но», «да», «вместе с тем»		рядоположенность, последовательность, равность, перечисление, одновременность
;	дизъюнкция слабая дизъюнкция сильная		соединительно- разделительный исключающе- разделительный	«или» «либо…либо»		выбор, альтернатива, вариантность
1	2		3	4		5
→, ⸧	импликация		условный	«если, то»		причинно-следственная связь, обусловленность, зависимость
≡, ↔, ← →	эквивалент-ность		взаимообуслов-ливающий	«если и только если», «тогда и только тогда, когда»		взаимозависимость, взаимообусловлен-ность, взаимодействие

Классификация сложных суждений.

Вид сложного суждения зависит от союза.

Общий вид: [(S –P)(«и», и «или», «либо, либо», «если, то..»)(S-P)],

или: p(&, 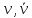, , 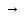≡) q
Основными видами сложных суждений являются:

Соединительное (или конъюктивные) сложное суждение (конъюнкция) образуется из двух или более простых суждений, соединенных логическим союзом конъюнкции (&, ˄, •).

Структура конъюнкции: [(S есть P) & (S есть P)] или на языке исчисления предикатов: p & q.

Союзы «а», «но», «да», «и» и др выражают конъюнкцию в естественном языке.

Например: «США – федеративное государство и оно состоит из 50 штатов». Данное суждение состоит из двух простых суждений («США – федеративное государство» и «оно состоит из 50 штатов») и соединительного союза «и».

В естественном языке конъюнктивные суждения могут принимать вид суждения со сложным объектом; S_1,S₂, S₃ есть Р.

Например: «Первая, вторая и третья курсовые работы являются исследованиями в области искусственного интеллекта».

Разъединительное (дизъюнктивное) сложное суждение (дизъюнкция) образуется из двух и более простых суждений.

Структура дизъюнкции: [(S есть P) 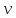(S есть P)]. Можно также записать:

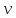p q. Дизъюнкции соответствуют союзы «либо либо», «или»и др.

Например: «Он является гением или он – сумасшедший». Данное суждение состоит из двух простых суждений («Он является гением» и «он – сумасшедший») и разделительного союза «или».

В логике различают слабую (неисключающую, нестрогую) и сильную (исключающую, строгую) дизъюнкцию. Слабая дизъюнкция выражается соединительно-разделительным союзом «или» и допускает истинность обоих простых суждений, которые она связывает. Например, «Любой человек знает стихи или хотя бы имя А.С Пушкина». Символически: p v q. Сильная дизъюнкция выражается соединительно-разделительным союзом «либо либо» и не допускает одновременной истинности входящих в ее состав простых суждений. Например, «Либо Вы сдаете задолженность, либо Вы будете отчислены». Символически: p 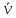q. Союз «либо» может выражаться и через союз «или», но по смыслу означать строгую дизъюнкцию.

Условное (импликативное) сложное суждение (импликация) образуется из двух и более простых суждений, соединенных логическим союзом импликации (→, ⸧).

Структура импликации (S есть P) → (S есть P), или p→q «если, то», «когда, тогда» и др

Например: «Если вы определились с темой курсового проекта, то можете приступать к работе».

В струкутуре импликативного суждения выделяют основание импликации (антецедент) и следствие импликации (консеквент).. Основание следует после слова «если». В нашем примере основание импликации «Если вы определились с темой курсового проекта». Следствие стоит после слова «то». В нашем примере следствие импликации: « Вы можете приступать к работе».

Условные суждения выражаются в естественном языке при помощи слов «если то», «только, если», «тогда, когда», «постольку, поскольку» и обозначают:

- причинно – следственную связь «Если лампу выключить, то она погаснет»;

- обоснование «Если фирма является экспертом, то она имеет лицензию».

Эквивалентные (взаимообусловленные) суждения (эквиваленция) состоят из двух и более простых суждений, связанных логическим союзом эквиваленции (≡, ↔, → ).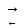

Структура эквиваленции: (S есть P) ≡ (S есть P) также можно записать:

p ≡ q «тогда и только тогда, когда» и др.

Например: « Золотая медаль присуждается учащемуся тогда, когда…»,

«если у данного прямоугольника стороны равны, то это – квадрат».

2. Установление логического значения сложных суждений при помощи таблиц истинности.
Условия истинности сложных суждений, состоящих из простых категорических суждений, основываются на допущении двузначности и задаются при помощи таблиц истинности.

Таблица истинности — это таблица, задающая логическую функцию.

2.1. Таблица истинности для конъюнкции:

p	q	p&q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

p, q – пропозициональные переменные, обозначающие простые суждения, т.е р – (S есть P) и q - (S есть P). Буква И означает истину, а буква Л означает ложь. Каждой строке таблицы соответствует сложное суждение.

Соединительные (конъюнктивные) суждения истинны тогда, когда истинны все входящие в них простые суждения (члены конъюнкции). Конъюнкция ложна, если ложен хотя бы один из ее членов.

2.2. Таблица истинности для дизъюнкции:

p	q	pvq
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

Слабая дизъюнкция истинна, когда истинен хотя бы один из членов дизъюнкции, и ложна, когда все ее члены – ложны.

2.2.1. Таблица

p	q	p q
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Сильная дизъюнкция истинна только при разных логических значениях членов дизъюнкции и ложна при одинаковых.

2.3 Таблица истинности для импликации:

p	q	p→q
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

Импликативные суждения истинны во всех случаях, кроме одного, когда антецедент – истинен, а консеквент – ложен. То есть в случае, когда причина возникла, а следствие не наступает, вся импликация является ложной.

2.4. Таблица истинности для эквиваленции:

p	q	pq
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Эквивалентные суждения являются равнозначными. Поэтому они истинны при равных значениях членов эквиваленции и ложны – при разных.

2.5.Таблица истинности для отрицания:

p	 p
И	Л
Л	И

«Отрицание» – унарный союз. Если исходное суждение истинно, то его отрицание – ложно, и наоборот. Сложное суждение может не только состоять из нескольких простых суждений, но и включать в себя несколько логических союзов: (p&q)→p. Чтобы установить истинность такого суждения, необходимо установить главный логический союз, указывающий на вид суждения, и построить соответствующую таблицу истинность:

2.6 Таблица

p	q	p&q	(p&q)→ p
И И Л Л	И Л И Л	И Л Л Л	И И И И

Главный логический союз (в данном случае – импликация) всегда находится в последней колонке таблицы.
3. Практические задания:
1. Установите вид следующих сложных суждений и определите их истинность при помощи таблиц истинности:
1.1. Редакция вправе увеличить или уменьшить размер гонорара.

- Дизъюнкция сильная (т.к. одновременно увеличить и уменьшить гонорар невозможно)

- Разъединительное сложное суждение

- Выражает: выбор

- Структура: p 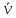q

Сильная дизъюнкция истинна только при разных логических значениях членов дизъюнкции. Ложна при одинаковых логических значениях

p	q	p q
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Выражение истинно.
1.2. Банан – пищевое растение и источник доходов для экспортирующих стран.

-Конъюнкция со сложным предикатом

- Соединительное сложное суждение

-Выражает: одновременность

-Структура: p&q

Соединительные (конъюнктивные) суждения истинны тогда, когда истинны все входящие в них простые суждения (члены конъюнкции). Конъюнкция ложна, если ложен хотя бы один из ее членов.

p	q	p&q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Выражение истинно.


1.3. Он сейчас находится в Минске или в Петербурге.

- Дизъюнкция сильная

- Разъединительное сложное суждение

- Выражает: альтернатив

- Структура: p 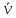q

Сильная дизъюнкция истинна только при разных логических значениях членов дизъюнкции. Ложна при одинаковых логических значениях

Предположим, что первая часть суждения истинна, значит, вторая - ложна, т.к. он не может одновременно находиться в разных городах.

p	q	p q
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Выражение истинно.
1.4. Кукушка хвалит петуха за то, что хвалит он кукушку.

- Импликация

- Условное сложное суждение

- Выражает: причинно-следственную связь

- Структура: p→q

p	q	p→q
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

Импликативные суждения истинны во всех случаях, кроме одного, когда антецедент – истинен, а консеквент – ложен. То есть в случае, когда причина возникла, а следствие не наступает, вся импликация является ложной.

Выражение истинно.
1.5. Если к двум прибавить два, то получится четыре.

- Импликация (суждения равнозначные)

- Условное сложное суждение

- Выражает: причинно-следственную связь

- Структура: p→q

p	q	p→q
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

Импликативные суждения истинны во всех случаях, кроме одного, когда антецедент – истинен, а консеквент – ложен. То есть в случае, когда причина возникла, а следствие не наступает, вся импликация является ложной.

Выражение истинно.
2. Постройте таблицу истинности для следующего выражения:

 (p → (pvq)).

p	q	pvq	p→(pvq)	┐(p→(pvq))
И	И	И	И	Л
И	Л	И	И	Л
Л	И	И	И	Л
Л	Л	Л	И	Л

Выражение является ложным. Главным логическим союзом данного выражения является (отрицание).

Литература

1) Малыхина, Г.И Логика : Учебник для вузов / Г. И. Малыхина. – Минск : Выш. шк., 2013. – 334 с.: ил.

2) Кириллов В. И., Старченко А. А. Логика: учебник для юридических вузов / под ред. проф. В. И. Кириллова. — Изд. 6-е, перераб. и доп. - М. : ТК Велби, Изд-во Проспект, 2008. - 240 с.

3) Бочаров В.А., Маркин В.И. Основы логики: Учебник. М.: ИНБ 87 ФРА-М, 19 9 8 .-2 9 6 с.
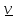