Пример оформления диплома. Теория к курсачу обновленное версия 3. 1 Общая часть 1 Краткая характеристика и описание технологического процесса

• Название: 1 Общая часть 1 Краткая характеристика и описание технологического процесса
• Анкор: Пример оформления диплома
• Дата: 25.09.2021
• Размер: 1.59 Mb.
• Имя файла: Теория к курсачу обновленное версия 3.docx
• Тип: Документы; #236857
• страница: 3 из 6

2.2.2 Расчет настроечных параметров системы автоматического регулирования
При выборе закона регулирования учитывают:

-свойства химико-технологического объекта времени;

-возможное максимальное возмущение;

-допустимый для технологического объекта вид переходного процесса;

Пропорционально – интегральный (ПИ) закон регулирования обеспечивает быстродействие, точность регулирования, возможность установки регулирующего органа в любом положение. Поэтому данные законы регулирования применяются достаточно широко в системах регулирования любых параметров.

ПИ – закон регулирования имеет передаточную функцию вида:

Пропорционально – интегрально – дифференциальный (ПИД) закон регулирования обеспечивает быстродействие, ускорение и точность регулирования. Следовательно, такие законы рекомендуется применять в объектах с большим временем запаздывания или инерционностью.

ПИД – закон регулирования имеет передаточную функцию вида:

Задача регулятора в АСР – обеспечить заданное изменение регулируемой величины. Динамические свойства регулятора определяются параметрами регулятора и могут изменяться в широких пределах. Задача определения настроечных параметров – обеспечение заданного критерия качества.

Степень колебательности

Приступаем к расчету расширенных ФЧХ (РФЧХ) и АЧХ (РАЧХ):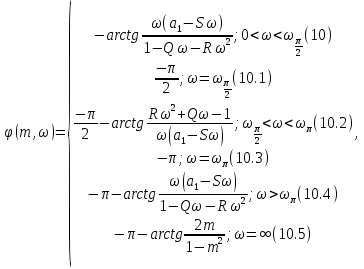

где

Q = а_1*m, (11)

Q = 19,3024* = 4,6519,

R=а_2*(1-m²), (12)

R = 94,4127*(1- ) = 88,9292,

S=2*а₂m, (13)

S = 2*94,4127* =45,5069,



(15)

Рассчитываем РАЧХ при тех же значениях, что и РФЧХ: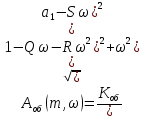

Результаты вычислений занесем в таблицу 2.2.
Для построения РФЧХ и РАЧХ вводим звено запаздывания.
A_з.з.(m,ω) = е^mωτ_об, (17)

φ_з.з.(m,ω)=-ωτ_{об ,} (18)
где m– степень колебательности ;

е – основание натурального логарифма;

ω– частота;

τ –время запаздывания.

Результаты вычислений занесем в таблицу 2.2.

Определим РАЧХ объекта со звеном запаздывания:
А_об.з(m, ω) = A_об*A_з.з., (19)
Результаты вычислений занесем в таблицу 2.2.

Определим РФЧХ объекта со звеном запаздывания:


φ_об.з(m, ω) =φ_об +φ_з.з., (20)
Результаты вычислений занесем в таблицу 2.2.
Таблица 2.2 - Данные для построения РФЧХ и РАЧХ объекта со звеном запаздывания

ω	φоб.	Aоб.	φз.з.	Aз.з	φоб.з.	Aоб.з.
0,02	-0,3994	3,6833	-0,072	1,0175	-0,4714	3,7478
0,04	-0,8056	3,5932	-0,144	1,0353	-0,9496	3,72
0,06	-1,1877	3,2498	-0,216	1,0534	-1,4037	3,4234
0,08	-1,524	2,7775	-0,288	1,0719	-1,812	2,9771
0,1	-1,8058	2,2963	-0,36	1,0906	-2,1658	2,5044
0,12	-2,0376	1,8723	-0,432	1,1097	-2,4696	2,0777
0,18	-2,5065	1,0322	-0,648	1,169	-3,1545	1,2067
0,2	-2,6115	0,8622	-0,72	1,1895	-3,3315	1,0256
0,26	-2,8382	0,5346	-0,936	1,253	-3,7742	0,6698
0,34	-3,0215	0,3185	-1,224	1,3431	-4,2455	0,4277
0,38	-3,0847	0,2556	-1,368	1,3905	-4,4527	0,3554
0,42	-3,136	0,2094	-1,512	1,4396	-4,6480	0,3014
0,44	-3,1574	0,1907	-1,584	1,4648	-4,7414	0,2794
0,46	-3,1776	0,1744	-1,656	1,4905	-4,8336	0,26
0,48	-3,1961	0,1601	-1,728	1,5166	-4,9241	0,2428
0,52	-3,2288	0,1363	-1,872	1,5701	-5,1008	0,214
0,54	-3,2434	0,1263	-1,944	1,5976	-5,1874	0,2017
0,56	-3,2568	0,1173	-2,016	1,6256	-5,2728	0,1907
0,6	-3,2811	0,102	-2,16	1,683	-5,4411	0,1717
	-3,612

По полученным данным строим расширенные ФЧХ (РФЧХ) и АЧХ (РАЧХ) объекта со звеном запаздывания рисунок 2.3.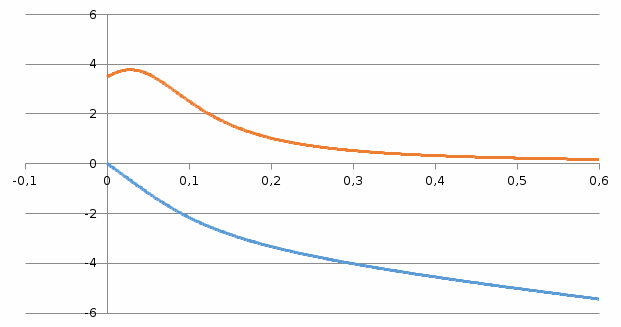



Рисунок 2.3 – Расширенные ФЧХ (РФЧХ) и АЧХ (РАЧХ) объекта со звеном запаздывания
Проводим расчет методом расширенных частотных характеристик. Метод расширенных частотных характеристик основан на амплитудно-фазовых частотных характеристиках (АЧФХ) ОУ и регулятора. Заменяя оператор Лапласа p на jω , определяем зависимость передаточной функции от частоты, после чего находим значения расширенных частот характеристик ПИД, ПИ-регулятора, зависящие от комплексных чисел.

Определяем граничные частоты для системы с ПИ-законом регулирования





По рисунку 2.3 выберем значения , и занесем в таблицу 2.3:
.
Определяем настроечные параметры ПИ – регулятора.

Для построения линии равного затухания определяем координаты точек К_р и К_р/Т_и.





Результаты вычислений занесем в таблицу 2.3.
Таблица 2.3–Данные для построения линии равного затухания

	φоб.з	Aоб.з.	γпи	Kp	Kp/Tu
0,06	-1,4037	3,4234	0,0702	0,0211	0,0183
0,08	-1,812	2,9771	0,4785	0,1591	0,0276
0,1	-2,1658	2,5044	0,8323	0,3037	0,035
0,12	-2,4696	2,0777	1,1361	0,449	0,038
0,14	-2,7303	1,7215	1,3968	0,5885	0,0343
0,16	-2,9561	1,4347	1,6226	0,716	0,0217
0,172	-3,0784	1,292	1,7449	0,7841	0,0088
0,176	-3,117	1,2485	1,7835	0,8053	0,0035

По полученным данным строим линию равного затухания рисунок 2.4.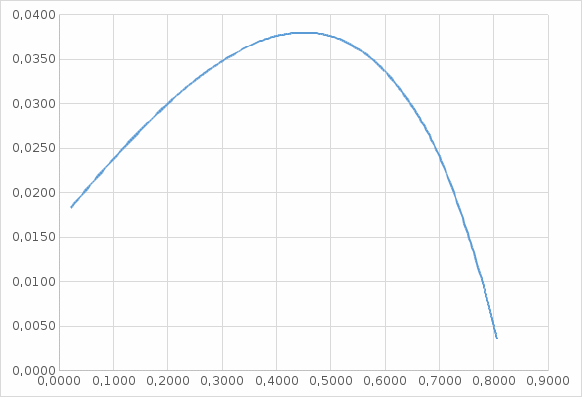

Рисунок 2.4 – Линия равного затухания
По линии равного затухания определяем оптимальные настроечные параметры ПИ – регулятора, которые определяет точка, лежащая правее её вершины.

K_р = 0,48684,

К_р/Т_и = 0,0376,
Определяем граничные частоты для системы с ПИД-законом регулирования







По рисунку 2.3 выберем значения , и занесем в таблицу 2.4:

Определяем предел изменения К_рТ_п:



В указанном интервале задаем значения : 3, 17, 26, 34, 40, 46.

Определяем настроечные параметры ПИД – закона регулирования по линий равного затухания (ЛРЗ).

Для построения линии равного затухания определяем координаты точек К_р и К_р/Т_и.





Результаты вычислений занесем в таблицу 2.4.
Таблица 2.4–Данные для построения семейства линий равного затухания

	φоб.з		Aоб.з		γпид		KpTп=3		KpTп=17
-3,3315-3,15451,20671,8211,08620,10072,30080,5806-2,95611,43471,62260,94740,10292,02700,4821-2,73031,72151,39680,79090,09661,73570,3869-2,46962,07771,13610,62260,08371,43230,2970-2,16582,50440,83230,44830,06671,12310,2148-1,8122,97710,47850,27480,04790,81460,1427-1,40373,42340,07020,10780,02970,51270,0830Kp/TuKpKp/Tu 0,2 0,18 0,16 0,14 0,12 0,1 0,08 0,06
KpTп=34KpTп=46Kp-3,49150,8812,1581,29010,06292,77470,77981,02291,9981,20440,08782,55400,6803Kp Продолжение таблицы 2.4 KpTп=26 0,22		Kp/Tu		Kp		Kp/Tu		Kp		Kp/Tu
0,7730		0,1173		1,0044		0,1478		1,3514		0,1935
1,1616		0,2037		1,4701		0,2578		1,9328		0,3391
1,5569		0,3101		1,9425		0,3947		2,5209		0,5217
1,9529		0,4342		2,4156		0,5560		3,1097		0,7389
2,3430		0,5735		2,8828		0,7394		3,6926		0,9883
2,7211		0,7259		3,3381		0,9426		4,2635		1,2677
3,0817		0,8892		3,7757		1,1634		4,8169		1,5748
3,4216		1,0612		4,1928		1,3998		5,3496		1,9077
3,7290		1,2407		4,5774		1,6504		5,8498		2,2649

По полученным данным строим линии равного затухания рисунок 2.5.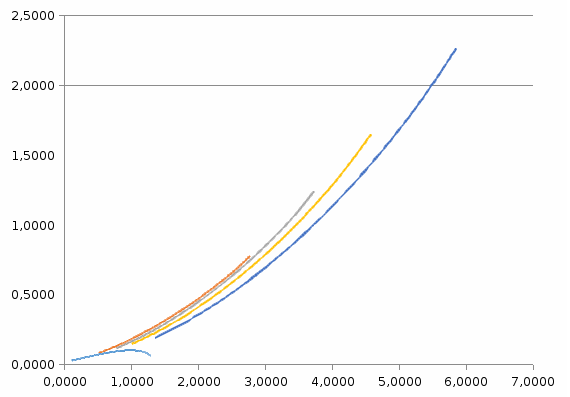


Рисунок 2.5 – Семейство линий равного затухания
По линии равного затухания определяем оптимальные настроечные параметры ПИД – регулятора, которые определяет точка, лежащая на самой ее вершине.

K_р = 5,8498,

К_р/Т_и = 2,2649,



где К_р - коэффициент передачи ПИД – регулятора;

T_и - постоянная времени изодрома,с,

T_п - постоянная времени предварения,с.