Пример оформления диплома. Теория к курсачу обновленное версия 3. 1 Общая часть 1 Краткая характеристика и описание технологического процесса
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
|
2.2.3 Оценка устойчивости и качества работы системы регулирования Для построения АФЧХ разомкнутой системы необходимо определить передаточную функцию разомкнутой системы. 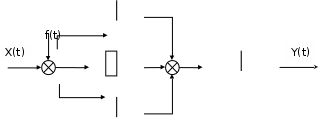 Рисунок 2.6 – Структурная схема разомкнутой системы Передаточная функция регулятора имеет вид (формула 9): Передаточная функция объекта имеет вид (формула 7): В системе автоматического регулирования (рисунок 2.6) объект и регулятор соединены последовательно, следовательно, математическое описание разомкнутой системы будет иметь вид: При определении устойчивости систем регулирования принято использовать критерии устойчивости. Наиболее распространенным является критерий устойчивости Найквиста, который позволяет по расположению корней характеристического уравнения и АФЧХ разомкнутой системы сделать заключение об устойчивости замкнутой системы. Для определения устойчивости разомкнутой системы выделим знаменатель из передаточной функции: Найдем корни характеристического уравнения (знаменателя): Таким образом, имеем один корень равен нулю, а два других отрицательные, то для определения устойчивости АСР воспользуемся вторым случаем критерия устойчивости Найквиста. В передаточной функции(формула 30) произведем замену p – оператор Лапласа на jω и умножим полученное выражение на сопряженное: 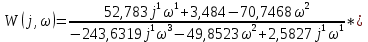 Определим значения действительной Ррс(ω) и мнимой Qрс(ω) частей, результаты расчетов занесем в таблицу 2.5. Таблица 2.5 – Данные для построения АФЧХ
По полученным данным строим АФЧХ разомкнутой системы с ПИД -регулированием (рисунок 2.7). 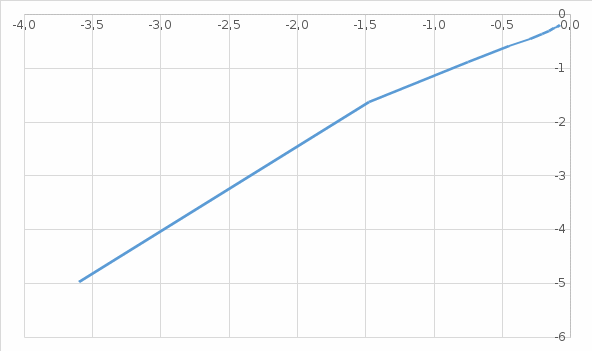 Рисунок 2.7 – АФЧХ разомкнутой системы с ПИД – регулированием Так как полученная АФЧХ разомкнутой системы не охватывает критическую точку с координатами [-1; j0], то замкнутая система является устойчивой. Для построения переходного процесса системы регулирования используем метод единичных трапеций. Построим и разобьём на трапеции ВЧХ замкнутой системы. Из концов отрезков, разбивающих ВЧХ, опустим перпендикуляры на ось ординат и получим трапеции[4]. Для построения ВЧХ замкнутой системы воспользуемся значениями 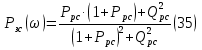 Построим ВЧХ замкнутой системы с ПИД- регулированием (формула 35). Значения Pрс(ω) и Qрс(ω) для расчета берём из таблицы 2.5. 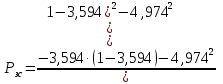 Результаты расчетов занесем в таблицу 2.6. Таблица 2.6 – Данные для построения ВЧХ
По полученным данным строим ВЧХ и разбиваем ее на трапеции рисунок 2.8. 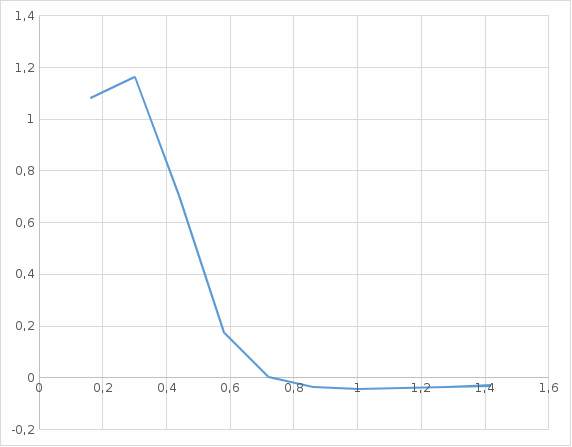 Рисунок 2.8 – ВЧХ замкнутой системы с ПИД – регулированием Получили 5 трапеций. Определяем параметры ωai, ωпi, Χi, Pi каждой трапеции и заносим их в таблицу 2.7. Вычисляем значение t и hi и заносим их в таблицу 2.7. Таблица 2.7– Построение переходной характеристики методом трапеций
Продолжение таблицы 2.7
По полученным данным строим семейство переходных характеристик (рисунок 2.9). 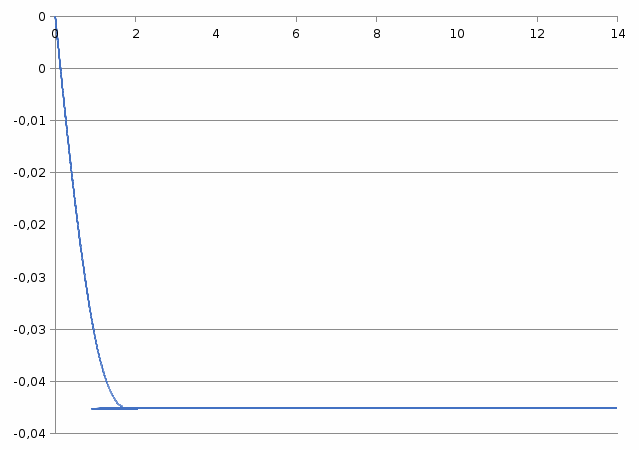 Рисунок 2.9 – Семейство переходных характеристик Для построения обобщенной переходной характеристики находим алгебраическую сумму всех составляющих hi(t) на выбранных интервалах времени: h(t) = h1(t) +h2(t) +h3(t)- h4(t)- h5(t) (36) Результаты заносим в таблицу 2.8. Таблица 2.8 – Данные для построения кривой переходного процесса
Продолжение таблицы 2.8
По полученным данным строим кривую переходного процесса замкнутой АСР (рисунок 2.10). 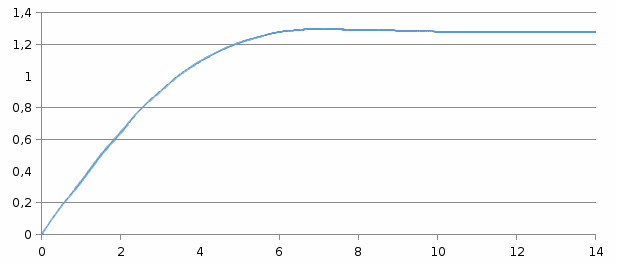 Рисунок 2.10 – Кривая переходного процесса с ПИД-регулированием Прямыми оценками качества переходного процесса называют показатели, определяемые непосредственно по кривой переходного процесса. В подавляющем большинстве случаев прямые оценки вводят по реакции системы на единичное ступенчатое воздействие, то есть по переходной функции САР. Эти показатели характеризуют длительность и колебательность переходных процессов. Получив кривую переходного процесса (рисунок 2.10) АСР, оцениваем качество регулирования [2]. Кривая получилась монотонная, поэтому определяем время регулирования, то есть время выхода к установившемуся значению выходной величины, tp =8c | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
