Факторный анализ-пример_вып. 1. Общий уровень знаний (уровень компетентности в области информатики и икт) з нестандартное творческое мышление (находить уникальные решения задач) т логика
 Скачать 70 Kb.
|
|
Факторный анализ (пример выполнения по информатике) 1. Общий уровень знаний (уровень компетентности в области информатики и икт) З 2. Нестандартное творческое мышление (находить уникальные решения задач) Т 3.Логика мышления (умение логически мыслить) Л 4. Состав (умение написать или найти ошибки в задачах на программирование и алгоритмы) С 5. Математическая компетентность (уровень понимания и умение применить знания) М testa = a (З) + b (Т) + с (Л) + d (С) + e (М) + Utesta З, Т, Л, С, М – аббревиатуры названий факторов; a, b, c, d, e, – коэффициенты регрессионного уравнения и Utesta – необъяснимая выделенными факторами доля вариации. З, Т, Л, С, М – общие факторы Utesta - уникальный фактор  где F’s – общие факторы, U – уникальный фактор, а A’s – коэффициенты комбинации k-факторов. Уникальный фактор не коррелирует с простыми переменными и с общими факторами. Итак, общее уравнение для оценки фактора Fj есть:  где Wi’s – называются оцененными факторными коэффициентами, а р – число переменных. Так как основной целью факторного анализа является выделение факторов, которые могут помочь объяснить существующие корреляционные связи между простыми переменными, хотя ясно, что переменные увязаны в каждый фактор с определенной степенью приближенности. Если корреляция между переменными мала, то похоже, что переменные не объединяться в форму общих факторов. Если мы заметим, что задания практически не коррелируют друг с другом, то есть часть теста не гомогенна и представляет собой просто набор различных заданий, которые не является тестом. Требования к матрице следующие: почти половина переменных должна коррелировать с коэффициентами, равными по значению 0.3 и более по абсолютной величине. Если какая-либо переменная имеет меньший коэффициент со всеми переменными, она исключается из факторного анализа. Если же это требование для этой переменной выполняется хотя бы для одной другой переменной из матрицы, следует оставить эту переменную в факторном анализе. Так же можно заметить линейную зависимость между факторами: Если ребенок(проверяемый) не усвоил основные понятия, то задания повышенного уровня сложности из части С он выполнит, скорее всего, на отрицательную оценку, так как все термины на базовом уровне необходимы для понимания, например, структуры программирования или алгоритмов. Так же можно привести пример содержательной линии «Объем информации и кодирование» и математическое мышление. Если ребенок (проверяемый) не способен решать математические примеры, то задания данного типа он так же не решит. Приведем примеры: Среди ранговых коэффициентов корреляции следует выделить коэффициент Спирмена, определяющийся по формуле: 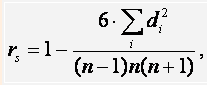 где di – разность соответствующих рангов величин X и Y, n – объём выборки. Коэффициент корреляции Спирмена обладает следующими свойствами: 1. Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь. 2.Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь. 3. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует. 4. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является  связь между измеряемыми величинами. Связь принято считать сильной, если  средней силы, если 0.3<|rs|<0.7 и слабой, если . Заметим, что существует и более тонкая градация силы связи, представленная шкалой Чертока, отображенной в таблице:
Проиллюстрируем на примере, как рассчитывается коэффициент корреляции Спирмена. Определим характер и силу связи между результатами ЕГЭ по информатике, используя данные из приведенной ниже таблицы.
Проранжируем имеющиеся данные в порядке их убывания и найдём квадраты разностей соответствующих рангов. Особое внимание следует обратить на то, что пятое и шестое место по информатике(1 вариант) делят два ученика, набравшие по 75 баллов. В этом случае для данных испытуемых следует присвоить ранг 5,5 (т.е. среднее арифметическое значение между 5 и 6). *Если достаточное число вариации объясняется общими факторами (более 70%), то все включаются в модель. Если же уникальный фактор забирает наибольшую вариацию, то нет общности измеряемых характеристик. В нашем примере таких факторов всего 6, причем около 65% вариации остается на уникальный фактор. Принудительное увеличение числа факторов прибавляет всего 3% вариации с каждым добавленным фактором.
Объём выборки n=10. Тогда: 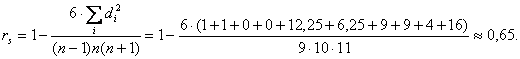 Следовательно, имеет место прямая связь средней силы. Использование коэффициента ранговой корреляции Спирмена очень удобно в силу относительной простоты его расчёта. Однако, в математической статистике показано, что коэффициент корреляции Спирмена применим не во всех случаях. Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины. В рассмотренном примере значения измеряемой величины изменяется практически равномерно, без явных «скачков». Т.е., если расположить оценки в порядке убывания, то каждая последующая оценка отличается от предыдущей примерно одинаково. Кроме того, отличие значений двух оценок по сравнению с самими оценками относительно невелико. Поэтому в данном примере целесообразно использовать коэффициент Спирмена. Главными целями факторного анализа являются: (1) сокращение числа переменных (редукция данных) и (2) определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется или как метод сокращения данных или как метод классификации. Следовательно, в нашем случае это необходимо по причине:
Термин «факторная структура» чаще всего относится к набору факторов, извлеченных в результате Ф. а. Некоторые из них являются общими факторами, разделяющими ответственность за изменение уровней изучаемых переменных, а некоторые — специфическими факторами, отвечающими за изменение уровня только какой-то одной (каждый — своей) переменной. Т. о., каждая переменная отображается в виде линейной комбинацией общих и специфического факторов. При описании результатов Ф. а. каждая переменная численно выражается через свою факторную нагрузку, указывающую на то, в какой степени определенный фактор «нагружен» этой переменной. Вывод:Факторные нагрузки изменяются в пределах от -1 до +1, т. к. они, фактически, являются коэффициентами корреляции между математически извлеченными факторами и приведенными к стандартизованному виду переменными. Так, например, если один фактор имеет нагрузку 0.80 на фактор «Логическое мышление», то говорят, что эти вопросы имеют высокую нагрузку(преобладание количества и сложности). То есть, нагрузка на факторы должна быть равномерной и иметь малую разность, чтобы тест был качественным и результаты были достоверными. |