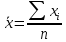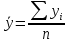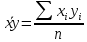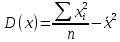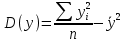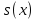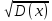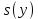|
|
1. Оценка уравнения регрессии
1. Оценка уравнения регрессии.
Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор s получается из выражения: s = (XTX)-1XTY
К матрице с переменными Xj добавляем единичный столбец:
1
|
4.8
|
11
|
1
|
3.7
|
13
|
1
|
3.9
|
15
|
1
|
4
|
17
|
1
|
5
|
18
|
1
|
4.8
|
19
|
1
|
5.3
|
19
|
1
|
5.4
|
20
|
1
|
4.4
|
20
|
1
|
6.8
|
21
|
1
|
6.7
|
21
|
1
|
6.4
|
22
|
1
|
6.9
|
22
|
1
|
7.2
|
25
|
1
|
7.3
|
28
|
1
|
8.2
|
29
|
1
|
8.1
|
30
|
1
|
8.6
|
31
|
1
|
9.6
|
32
|
1
|
9.7
|
36
|
Матрица Y
7
|
7
|
7
|
7
|
7
|
7
|
8
|
8
|
8
|
10
|
9
|
11
|
9
|
11
|
12
|
12
|
12
|
12
|
14
|
14
|
Матрица XT
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
4.8
|
3.7
|
3.9
|
4
|
5
|
4.8
|
5.3
|
5.4
|
4.4
|
6.8
|
6.7
|
6.4
|
6.9
|
7.2
|
7.3
|
8.2
|
8.1
|
8.6
|
9.6
|
9.7
|
11
|
13
|
15
|
17
|
18
|
19
|
19
|
20
|
20
|
21
|
21
|
22
|
22
|
25
|
28
|
29
|
30
|
31
|
32
|
36
|
Умножаем матрицы, (XTX)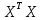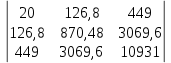
  
В матрице, (XTX) число 20, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы XT и 1-го столбца матрицы X
Умножаем матрицы, (XTY)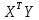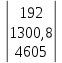
 
Находим обратную матрицу (XTX)-1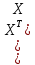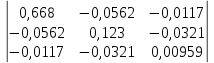
 
Вектор оценок коэффициентов регрессии равен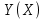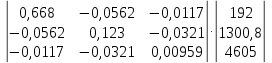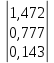
  
Уравнение регрессии (оценка уравнения регрессии)
Y = 1.4718 + 0.7767X1 + 0.1427X2
2. Матрица парных коэффициентов корреляции R.
Число наблюдений n = 20. Число независимых переменных в модели равно 2, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 4. Матрица, независимых переменных Х имеет размерность (20 х 4).
Матрица A, составленная из Y и X
1
|
7
|
4.8
|
11
|
1
|
7
|
3.7
|
13
|
1
|
7
|
3.9
|
15
|
1
|
7
|
4
|
17
|
1
|
7
|
5
|
18
|
1
|
7
|
4.8
|
19
|
1
|
8
|
5.3
|
19
|
1
|
8
|
5.4
|
20
|
1
|
8
|
4.4
|
20
|
1
|
10
|
6.8
|
21
|
1
|
9
|
6.7
|
21
|
1
|
11
|
6.4
|
22
|
1
|
9
|
6.9
|
22
|
1
|
11
|
7.2
|
25
|
1
|
12
|
7.3
|
28
|
1
|
12
|
8.2
|
29
|
1
|
12
|
8.1
|
30
|
1
|
12
|
8.6
|
31
|
1
|
14
|
9.6
|
32
|
1
|
14
|
9.7
|
36
|
Транспонированная матрица.
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
7
|
7
|
7
|
7
|
7
|
7
|
8
|
8
|
8
|
10
|
9
|
11
|
9
|
11
|
12
|
12
|
12
|
12
|
14
|
14
|
4.8
|
3.7
|
3.9
|
4
|
5
|
4.8
|
5.3
|
5.4
|
4.4
|
6.8
|
6.7
|
6.4
|
6.9
|
7.2
|
7.3
|
8.2
|
8.1
|
8.6
|
9.6
|
9.7
|
11
|
13
|
15
|
17
|
18
|
19
|
19
|
20
|
20
|
21
|
21
|
22
|
22
|
25
|
28
|
29
|
30
|
31
|
32
|
36
|
Матрица XTX.
20
|
192
|
126.8
|
449
|
192
|
1958
|
1300.8
|
4605
|
126.8
|
1300.8
|
870.48
|
3069.6
|
449
|
4605
|
3069.6
|
10931
|
Полученная матрица имеет следующее соответствие:
∑n
|
∑y
|
∑x1
|
∑x2
|
∑y
|
∑y2
|
∑x1 y
|
∑x2 y
|
∑x1
|
∑yx1
|
∑x1 2
|
∑x2 x1
|
∑x2
|
∑yx2
|
∑x1 x2
|
∑x2 2
|
Найдем парные коэффициенты корреляции.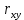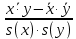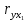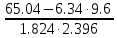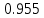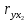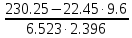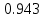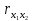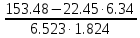
 
  
  
  
Признаки x и y
|
∑xi
|
|
∑yi
|
|
∑xi∙yi
|
|
Для y и x1
|
126.8
|
6.34
|
192
|
9.6
|
1300.8
|
65.04
|
Для y и x2
|
449
|
22.45
|
192
|
9.6
|
4605
|
230.25
|
Для x1 и x2
|
449
|
22.45
|
126.8
|
6.34
|
3069.6
|
153.48
|
Дисперсии и среднеквадратические отклонения.
Признаки x и y
|
|
|
 
|
 
|
Для y и x1
|
3.328
|
5.74
|
1.824
|
2.396
|
Для y и x2
|
42.548
|
5.74
|
6.523
|
2.396
|
Для x1 и x2
|
42.548
|
3.328
|
6.523
|
1.824
|
Матрица парных коэффициентов корреляции R:
-
|
y
|
x1
|
x2
|
y
|
1
|
0.9554
|
0.9426
|
x1
|
0.9554
|
1
|
0.9367
|
x2
|
0.9426
|
0.9367
|
1
| |
|
|
Скачать 22.65 Kb.