1. Оценка уравнения регрессии
 Скачать 22.65 Kb. Скачать 22.65 Kb.
|
|
Частные коэффициенты корреляции. Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и xi) при условии, что влияние на них остальных факторов (xj) устранено. На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели. 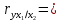 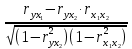 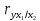  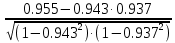  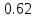 Теснота связи умеренная 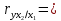 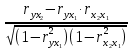 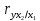  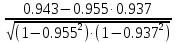  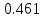 Теснота связи не сильная 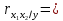 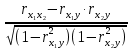 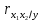  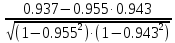  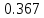 Теснота связи не сильная Анализ мультиколлинеарности. 1. Анализ мультиколлинеарности на основе матрицы коэффициентов корреляции. Если в матрице есть межфакторный коэффициент корреляции rxjxi > 0.7, то в данной модели множественной регрессии существует мультиколлинеарность. В нашем случае r(x1x2) имеют |r|>0.7, что говорит о мультиколлинеарности факторов и о необходимости исключения одного из них из дальнейшего анализа. 2. Ридж-регрессия. Наиболее детальным показателем наличия проблем, связанных с мультиколлинеарностью, является коэффициент увеличения дисперсии, определяемый для каждой переменной как: 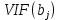  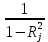 где Rj2 коэффициент множественной детерминации в регрессии Xj на прочие X. О мультиколлинеарности будет свидетельствовать VIF от 4 и выше хотя бы для одного j. 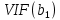  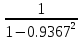  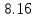 Поскольку VIF(b)1 ≥ 4, что говорит о мультиколлинеарности факторов x1, x2 и о необходимости исключения одного из них из дальнейшего анализа. Критерием плохой обсуловленности является высокая величина отношения λmax/λmin максимального и минимального собственных чисел матрицы XTX — называемого показателем обусловленности. Это соотношение также позволяет судить о степени серьезности проблем мультиколлинеарности: показатель обусловленности в пределах от 10 до 100 свидетельствует об умеренной коллинеарности, свыше 1000 — об очень серьезной коллинеарности. Модель регрессии в стандартном масштабе. Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам: 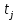  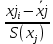 где хji - значение переменной хji в i-ом наблюдении. 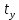  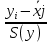 Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение S. Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением: ty = ∑βjtxj Для оценки β-коэффициентов применим МНК. При этом система нормальных уравнений будет иметь вид: rx1y=β1+rx1x2•β2 + ... + rx1xm•βm rx2y=rx2x1•β1 + β2 + ... + rx2xm•βm ... rxmy=rxmx1•β1 + rxmx2•β2 + ... + βm Для наших данных (берем из матрицы парных коэффициентов корреляции): 0.955 = β1 + 0.937β2 0.943 = 0.937β1 + β2 Данную систему линейных уравнений решаем методом Гаусса: β1 = 0.591; β2 = 0.389; Искомое уравнение в стандартизованном масштабе: ty=β1tx1+β2tx2 Расчет β-коэффициентов можно выполнить и по формулам: 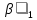  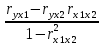  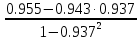  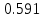 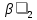  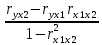  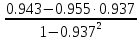  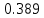 Стандартизированная форма уравнения регрессии имеет вид: ty = 0.591x1 + 0.389x2 Найденные из данной системы β–коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам: 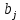  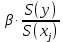 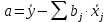 3. Анализ параметров уравнения регрессии. Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации Для несмещенной оценки дисперсии проделаем следующие вычисления: Несмещенная ошибка ε = Y - Y(x) = Y - X∙s (абсолютная ошибка аппроксимации)
Средняя ошибка аппроксимации 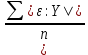 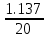 Оценка дисперсии равна: se2=(Y-Y(X))T(Y-Y(X))=7.886 Несмещенная оценка дисперсии равна: 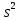  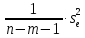  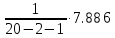  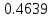 Оценка среднеквадратичного отклонения (стандартная ошибка для оценки Y): 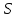  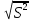  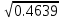  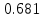 Найдем оценку ковариационной матрицы вектора k = S2 • (XTX)-1 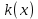  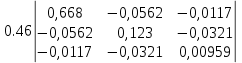  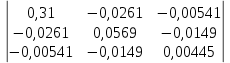 Дисперсии параметров модели определяются соотношением S2i = Kii, т.е. это элементы, лежащие на главной диагонали 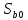  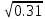  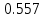 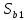  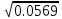  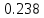 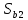  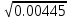  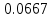 Показатели тесноты связи факторов с результатом. Если факторные признаки различны по своей сущности и (или) имеют различные единицы измерения, то коэффициенты регрессии bj при разных факторах являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям тесноты связи относят: частные коэффициенты эластичности, β–коэффициенты, частные коэффициенты корреляции. |
