1. Оценка уравнения регрессии

• Название: 1. Оценка уравнения регрессии
• Дата: 25.12.2020
• Размер: 22.65 Kb.
• Имя файла: 681678375.docx
• Тип: Документы; #164284
• страница: 3 из 3

Частные коэффициенты эластичности.

С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле: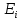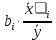



Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат у с увеличением признака-фактора х_j на 1% от своего среднего уровня при фиксированном положении других факторов модели.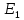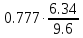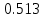



Частный коэффициент эластичности |E₁| < 1. Следовательно, его влияние на результативный признак Y незначительно.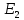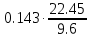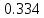



Частный коэффициент эластичности |E₂| < 1. Следовательно, его влияние на результативный признак Y незначительно.

Стандартизированные частные коэффициенты регрессии.

Стандартизированные частные коэффициенты регрессии - β-коэффициенты (β_j) показывают, на какую часть своего среднего квадратического отклонения S(у) изменится признак-результат y с изменением соответствующего фактора х_j на величину своего среднего квадратического отклонения (S_хj) при неизменном влиянии прочих факторов (входящих в уравнение).

По максимальному β_j можно судить, какой фактор сильнее влияет на результат Y.

По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.

Коэффициент β_j может также интерпретироваться как показатель прямого (непосредственного) влияния j-ого фактора (x_j) на результат (y). Во множественной регрессии j-ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели).

Косвенное влияние измеряется величиной: ∑β_ir_xj,xi, где m - число факторов в модели. Полное влияние j-ого фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата - r_xj,y.

Так для нашего примера непосредственное влияние фактора x₁ на результат Y в уравнении регрессии измеряется β_j и составляет 0.591; косвенное (опосредованное) влияние данного фактора на результат определяется как:

r_x1x2β₂ = 0.937 ∙ 0.389 = 0.364

Сравнительная оценка влияния анализируемых факторов на результативный признак.

5. Сравнительная оценка влияния анализируемых факторов на результативный признак производится:

- средним коэффициентом эластичности, показывающим на сколько процентов среднем по совокупности изменится результат y от своей средней величины при изменении фактора x_i на 1% от своего среднего значения;

- β–коэффициенты, показывающие, что, если величина фактора изменится на одно среднеквадратическое отклонение S_xi, то значение результативного признака изменится в среднем на β своего среднеквадратического отклонения;

- долю каждого фактора в общей вариации результативного признака определяют коэффициенты раздельной детерминации (отдельного определения): d²_i = r_yxiβ_i.

d²₁ = 0.96∙0.591 = 0.565

d²₂ = 0.94∙0.389 = 0.366

При этом должно выполняться равенство:

∑{d{\sub i}²} = R² = 0.931

Множественный коэффициент корреляции (Индекс множественной корреляции).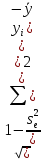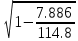



Коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции: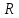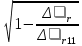



где Δ_r - определитель матрицы парных коэффициентов корреляции; Δ_r11 - определитель матрицы межфакторной корреляции.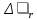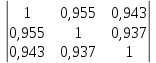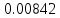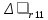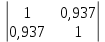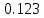





Коэффициент множественной корреляции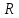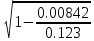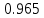



Аналогичный результат получим при использовании других формул: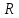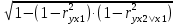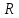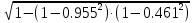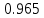





Связь между признаком Y и факторами X_i сильная

Расчёт коэффициента корреляции выполним, используя известные значения линейных коэффициентов парной корреляции и β-коэффициентов.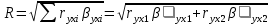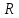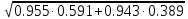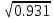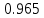





Коэффициент детерминации

R² = 0.931

Коэффициент детерминации.

R²= 0.965² = 0.9313

Более объективной оценкой является скорректированный коэффициент детерминации: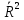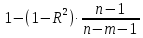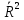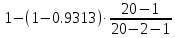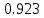





Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение Y.

Добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.

5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).

Число v = n - m - 1 называется числом степеней свободы. Считается, что при оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений, по крайней мере, в 3 раза превосходило число оцениваемых параметров.

1) t-статистика

T_табл (n-m-1;α/2) = (17;0.025) = 2.458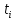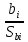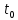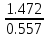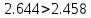





Статистическая значимость коэффициента регрессии b₀ подтверждается.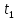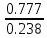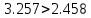



Статистическая значимость коэффициента регрессии b₁ подтверждается.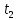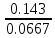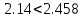



Статистическая значимость коэффициента регрессии b₂ не подтверждается.

Доверительный интервал для коэффициентов уравнения регрессии.

Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:

(b_i - t_i∙S_bi; b_i + t_i∙S_bi)

b₀: (1.472 - 2.458∙0.557 ; 1.472 + 2.458∙0.557) = (0.103;2.84)

b₁: (0.777 - 2.458∙0.238 ; 0.777 + 2.458∙0.238) = (0.191;1.363)

b₂: (0.143 - 2.458∙0.0667 ; 0.143 + 2.458∙0.0667) = (-0.0212;0.307)

6. Проверка общего качества уравнения множественной регрессии.

F-статистика. Критерий Фишера.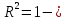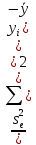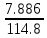



Проверим гипотезу об общей значимости - гипотезу об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:

H₀: R² = 0; β₁ = β₂ = ... = β_m = 0.

H₁: R² ≠ 0.

Проверка этой гипотезы осуществляется с помощью F-статистики распределения Фишера (правосторонняя проверка).

Если F < F_kp = F_{α ; n-m-1}, то нет оснований для отклонения гипотезы H₀.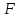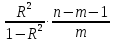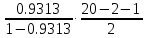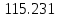



Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 20 - 2 - 1 = 17, Fkp(2;17) = 3.59

Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно (т.е. коэффициенты b_i совместно значимы).

Оценка значимости дополнительного включения фактора (частный F-критерий).

Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличить долю объясненной вариации результативного признака. Это может быть связано с последовательностью вводимых факторов (т. к. существует корреляция между самими факторами).

Мерой оценки значимости улучшения качества модели, после включения в нее фактора х_j, служит частный F-критерий – F_xj: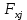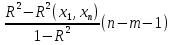



где m – число оцениваемых параметров.

В числителе - прирост доли вариации у за счет дополнительно включенного в модель фактора х_j.

Если наблюдаемое значение F_xj больше F_kp, то дополнительное введение фактора x_j в модель статистически оправдано.

Частный F-критерий оценивает значимость коэффициентов «чистой» регрессии (b_j). Существует взаимосвязь между частным F-критерием - F_xj и t-критерием, используемым для оценки значимости коэффициента регрессии при j-м факторе: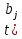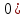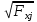



Оценим с помощью частного F-критерия:

1) целесообразность включения в модель регрессии факторов х₁ после введения х_j (F_x1).

Определим наблюдаемое значение частного F-критерия: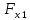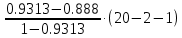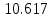



R²(x₂,x_n) = r²(x₂) = 0.9426² = 0.888

F_kp(k1=1;k2=17) = 4.45

Сравним наблюдаемое значение частного F-критерия с критическим:

F_x1>4.45, следовательно, фактор х₁ целесообразно включать в модель после введения фактора х₂.

2) целесообразность включения в модель регрессии факторов х₂ после введения х_j (F_x2).

Определим наблюдаемое значение частного F-критерия: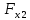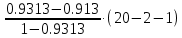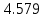



R²(x₁,x_n) = r²(x₁) = 0.9554² = 0.913

Сравним наблюдаемое значение частного F-критерия с критическим:

F_x2>4.45, следовательно, фактор х₂ целесообразно включать в модель после введения фактора х₁.

Выводы.

В результате расчетов было получено уравнение множественной регрессии: Y = 1.4718 + 0.7767X₁ + 0.1427X₂. Возможна экономическая интерпретация параметров модели: увеличение X₁ на 1 ед.изм. приводит к увеличению Y в среднем на 0.777 ед.изм.; увеличение X₂ на 1 ед.изм. приводит к увеличению Y в среднем на 0.143 ед.изм. По максимальному коэффициенту β₁=0.591 делаем вывод, что наибольшее влияние на результат Y оказывает фактор X₁. Статистическая значимость уравнения проверена с помощью коэффициента детерминации и критерия Фишера. Установлено, что в исследуемой ситуации 93.13% общей вариабельности Y объясняется изменением факторов X_j. Установлено также, что параметры модели статистически не значимы.
Решение было получено и оформлено с помощью сервиса:

Уравнение множественной регрессии

Вместе с этой задачей решают также:

Уравнение парной линейной регрессии

Выявление тренда методом аналитического выравнивания

Уравнение нелинейной регрессии

Проверка на автокорреляцию

Системы эконометрических уравнений

Метод статистических уравнений зависимостей