1. Окрестность точки на числовой прямой. Предел функции в точке. Предел в бесконечно удаленной точке. Геометрическая интерпретация предела
 Скачать 0.52 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
f(x) = f(x0), | (1) |
т.е.
| | O( f(x0) ) O(x0) : x O(x0) f(x) O( f(x0) ) . | |
Замечание. Равенство (1) можно записать в виде:
| |
f(x) = f (
x ), | |
т.е. под знаком непрерывной функции можно переходить к пределу.
Пусть Δx = x − x0 — приращение аргумента, Δy = f(x) − f(x0 ) — соответствующее приращение функции.
Необходимое и достаточное условие непрерывности функции в точке
Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда
| |
Δy = 0. | (2) |
Замечание. Условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.
Пусть функция f(x) определена в полуинтервале [x0, x0 + δ ).
Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел
| |
f(x) = f(x0). | |
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].
Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
| |
f(x) = f(x0). |
2) Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
| | | |
| Непрерывна при x = a. | | Имеет разрыв при x = a. |
| | | |
| Непрерывна при x = a. | | Имеет разрыв при x = a. |
| Рисунок 1. | ||
3) Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел и правосторонний предел ;
Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
4. Предел функции в точке. Единственность предела.
1)Число называется пределом функции в точке , если для такое, что для из того, что следует, что : или при .
2) Теорема о единственности предела
Формулировка:
Если функция в точке имеет предел, то этот предел единственный.
Доказательство:
Докажем методом от противного. Предположим, что , , . Возьмём , по определению и свойству окрестности найдётся такая проколотая -окрестность точки (), в которой одновременно будут выполнятся неравенства , , тогда в точках этой же окрестности . Получили противоречие . Отсюда, функция в точке имеет единственный предел.
5. Бесконечно малые функции в точке. Теоремы о бесконечно малых.
1) Функция называется бесконечно малой функцией (б.м.ф.) при (или в точке ), если
2)Теорема 1. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
Доказательство. Пусть – бесконечно малая последовательность. Это означает, что для любого положительного числа существует такой номер N, что для всех номеров выполняется условие , где С – любое действительное число. Тогда <
< , а это и означает, что последовательность – бесконечно малая.
Теорема 2. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть и – бесконечно малые последовательности. Это означает, что для любого числа существуют такие номера и , что для всех номеров и для всех номеров выполняются условия и соответственно. Тогда для всех номеров выполняется условие, а это и означает, что последовательность – бесконечно малая.
Следствие 1. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие 2. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 3. Бесконечно малая последовательность ограничена.
Доказательство. Пусть – бесконечно малая последовательность, ε>0 – некоторое число, а N – номер, начиная с которого выполняется условие . Обозначим через М наибольшее из следующих чисел . Очевидно, что для любого номера n, а это и означает, что последовательность {} – ограничена.
Теорема 4. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
Доказательство. Пусть – ограниченная, а – бесконечно малая последовательности. Это означает, что существует число М>0 такое, что для любого номера n выполняется , и для любого числа существует номер N такой, что для всех номеров выполняется . Тогда для всех номеров и любого ε>0 выполняется , а это и означает, что последовательность – бесконечно малая.
Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 5. Если элементы бесконечно малой последовательности равны одному и тому же числу С, то С=0.
Доказательство. Предположим, что . Для существует такой номер N, что для всех номеров выполняется . Так как , а , то последнее неравенство имеет вид , откуда . Полученное противоречие показывает, что предположение неверно, следовательно, .
Теорема 6. Если – бесконечно большая последовательность то, начиная с некоторого номера n, определена последовательность , которая является бесконечно малой. Если не все элементы бесконечно малой последовательности равны нулю, то последовательность бесконечно большая.
Доказательство. Пусть – бесконечно большая последовательность. Это означает, что для любого положительного числа М можно указать такой номер N, что для всех номеров выполняется . А это означает, что при все элементы , а поэтому последовательность имеет смысл с номера N. Пусть - любое положительное число. Для числа можно указать номер такой, что для nN выполняется . Это и означает, что – бесконечно малая. Доказательство второй части теоремы проводится аналогично.
Рассмотрим теперь лемму, которая будет использоваться при доказательстве некоторых теорем.
Лемма. Для того чтобы число а являлось пределом последовательности , необходимо и достаточно, чтобы имел вид , n=1,2,…, где есть бесконечно малая последовательность.
Доказательство. Обозначим . Условие по определению предела равносильно тому, что для любого числа существует такой номер N, что для всех номеров выполняется неравенство , то есть , а это и равносильно тому, что .
Эта лемма показывает особую роль бесконечно малых последовательностей при изучении предела последовательности. Перейдем теперь непосредственно к рассмотрению простейших свойств пределов числовых последовательностей.
6. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
1) Пусть и — бесконечно малые при .
1. Если , то говорят, что является бесконечно малой высшего порядка по сравнению с . В этом случае пишут .
2. Если , где —число, отличное от нуля, то говорят, что и — бесконечно малые одного и того же порядка. В часности, если , то бесконечно малые и называются эквивалентными. Запись означает, что и —эквивалентные бесконечно малые.
Если , то это означает, что . Таким образом, является бесконечно малой высшего порядка по сравнению с , т. е.
3. Если и —бесконечно малые одного и того же порядка, причем , то говорят, что бесконечно малая имеет порядок по сравнению с .
Отметим некоторые свойства бесконечно малых величин:
1o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если , то и .
2o. Бесконечно малые и эквивалентны тогда и только тогда, когда их разность является бесконечно малой высшего порядка по сравнению с и , т. е. если , .
3o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если
, , , то .
2) Б.м. функции и называются эквивалентными или равносильными б.м. одного порядка при , если
Обозначают: при .
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть - бесконечно малая при .
7. Теорема о предельном переходе под знаком неравенства. Теорема о сжатой
переменной (формулировка).
1) ТЕОРЕМА: (о предельном переходе в неравенстве.).
Пусть при всех n выполняется неравенство ,и переменные и имеют пределы:
;
Тогда:, т. е. .
Теорема означает, что в неравенстве можно переходить к пределам, сохраняя знак неравенства.
Доказательство:
Предположим, что
Выделим вокруг точек и столь малые E – окрестности, чтобы они не пересекались.
По определению предела, начиная с некоторого номера n, переменные и попадут в свои E – окрестности предельных точек.
Это означает, что, начиная с некоторого номера n, что противоречит условию. Противоречие доказывает теорему, ч. т. д.
Замечание:
Если при всех n выполняется (строго), то гарантировать строгого неравенства в пределе нельзя (в общем случае), гарантируется лишь нестрогое неравенство.
2) ТЕОРЕМА: (о сжатой переменной).
Пусть, начиная с некоторого , выполняются неравенства , причем крайние переменные имеют одинаковый конечный предел , тогда переменная также имеет предел, причем тот же самый.
8. Теорема о сохранении знака функции. Теорема о связи функции, имеющей
конечный предел, с бесконечно малой.
1) Теорема. (Теорема о сохранении знака непрерывной функции). Если
, 
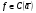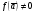, то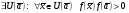 
.Доказательство. Достаточно доказать, что если
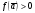, то и 
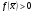. Действительно, взяв
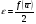получаем по определению непрерывности окрестность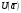 
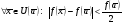
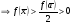. 2) Теорема Для того, чтобы функция
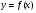имела предел в точке aравный А, необходимо и достаточно, чтобы имело место представление :
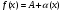, где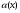 
- бесконечно малая функция в точке a .ДОК. (1) Если
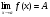, то функция 
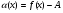б.м.ф. Действительно,
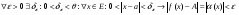(2) 
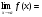
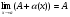.9. Односторонняя непрерывность. Непрерывность функции на отрезке. Теоремы
Больцано-Коши и Вейерштрасса (без доказательства).
1) Определение односторонней непрерывности.
В определении непрерывности функции в точке х0 требуется существование и равенство . С применением односторонних пределов определяются понятия непрерывности функции в точке слева и справа:
Опр.. Функция f(x) называется непрерывной в точке х0 слева, если .
Опр. Функция f(x) называется непрерывной в точке х0 справа, если .
Опр. Если одно из этих условий не выполнено, то функция f(x) имеет в точке х0 разрыв, соответственно, слева или справа.
Если функция определена на отрезке [a,b], то в левом конце отрезка х0= a можно говорить только о непрерывности справа, в правом конце (х0= b) - о непрерывности слева. Для внутренней точки отрезка функция f(x) непрерывна в точке х0 тогда и только тогда, когда она непрерывна в этой точке слева и справа
2) Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
3) Теорема Больцано — Коши
Пусть дана непрерывная функция на отрезке Пусть также и без ограничения общности предположим, что Тогда для любого существует такое, что
Теорема Вейерштрасса
Теорема Вейерштрасса об ограниченной возрастающей последовательности утверждает, что любая ограниченная возрастающая последовательность имеет предел, причем этот предел равен ее точной верхней грани. Несмотря на простоту доказательства, эта теорема оказывается очень удобной для нахождения пределов многих последовательностей, или хотя бы доказательства их существования.
10. Производная функция в точке. Геометрическая и механическая интерпретация.
1) Определение. Производной функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
.
2) Геометрическая интерпретация
Обратимся к рисунку 1, на котором представлен фрагмент графика функции .
Рис. 1. Секущая AB образует угол β с положительным направлением оси 0x. Касательная к графику функции проведена в точке A.
Угловой коэффициент секущей AB равен средней скорости изменения функции на промежутке [x, x + ∆x]:
| | | (5) | |
Предельным положением секущей AB при перемещении точки B к точке A по дуге кривой является касательная к графику в точке A. Поэтому угловой коэффициент касательной равен пределу углового коэффициента секущей при ∆x → 0:
| | | (6) | |
Рис. 2. Касательная является предельным положением секущей AB при перемещении точки B к точке A.
Таким образом, производная в точке x равна тангенсу угла, образованного касательной к графику функции в этой точке с положительным направлением оси 0x.
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + точка перемещается на расстояние:x ( t0 + ) x ( t0 ) = , а её средняя скорость равна:va= . При 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0) материальной точки в момент времени t0 . Но по определению производной мы имеем:
отсюда, v ( t0) = x’ ( t0) , т.e. скорость – это производная координатыповремени. В этом и состоит механический смысл производной.Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).
11. Дифференцируемые функции. Необходимое и достаточное условие
дифференцируемости. Дифференциал. Непрерывность дифференцируемой
функции.
1) Дифференци́руемаяфу́нкция в математическом анализе — это функция, которая может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат.
2) Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке.
При этом
| | Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx, | |
где α(Δx) - бесконечно малая функция, при Δx→0.
3) Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции.
4) Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).
Доказательство
Возьмем произвольное фиксированное число x (a,b).
По условию теоремы
Следовательно, в малой окрестности числа x0 можно определить функцию α = α(Δx), стремящуюся к нулю при такую, что
Но тогда и, следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция fнепрерывна на всем интервале (a, b).
Теорема доказана.
12. Производная функции в точке. Правила дифференцирования суммы,
произведения и частного.
1) Определение. Производной функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
.
2) Правила дифференцирования суммы, произведения и частного
Теорема
Если функции u=u(x) и v=v(x) имеют в точке x производные, то сумма (разность), произведение и частное этих функций также имеют производные в этой точке, и справедливы следующие формулы:
1) (u±v)/=u/±v/ ,
2) (u·v)/=u/v+v/u ,
3) (vu)=v2u/v−v/u .
Доказательство
Из определения производной:
(u±v)/=limΔx→0Δx[u(x+Δx)±v(x+Δx)]−[u(x)±v(x)]= =limΔx→0Δx[u(x+Δx)−u(x)]±[v(x+Δx)−v(x)]= .
=limΔx→0Δxu(x+Δx)−u(x)±limΔx→0Δxv(x+Δx)−v(x)=u/±v/
(u·v)/=limΔx→0Δxu(x+Δx)·v(x+Δx)−u(x)·v(x)±v(x+Δx)·v(x)= limΔx→0Δxu(x+Δx)[v(x+Δx)−v(x)]+
+limΔx→0Δxv(x)[u(x+Δx)−u(x)]=uv/+vu/.
(vu)/=limΔx→0Δxv(x+Δx)u(x+Δx)−v(x)u(x)=limΔx→0Δx·v(x+Δx)·v(x)u(x+Δx)·v(x)−u(x)·v(x+Δx)±u(x)·v(x)=v2u/v−v/u.
Теорема доказана.
13. Теорема Ферма.
Для любого натурального числа уравнение
не имеет натуральных решений , и .
14. Теорема Ролля
Теорема. Пусть функция дифференцируема в открытом промежутке , на концах этого промежутка сохраняет непрерывность и принимает одинаковые значения: . Тогда существует точка , в которой производная функции равна нулю: .
Рис. 3. Теорема Ролляустанавливает условия существования хотя бы одной точки c, в которой касательная к графику функции параллельна оси 0x. Таких точек может быть несколько.
Доказательство. Если в промежутке , то во всех точках этого промежутка. Иначе наибольшее значение M функции превышает ее наименьшее значение m в промежутке . Поскольку на концах этого промежутка функция принимает одинаковые значения, то по крайней мере одно из значений, M или m, достигается во внутренней точке c промежутка . Тогда по теореме Ферма .
15. Теорема Лагранжа
Теорема. Пусть функция дифференцируема в открытом промежутке и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка , что
| | | (13) | |
Доказательство. Рассмотрим вспомогательную функцию
Эта функция непрерывна и дифференцируема в промежутке , а на его концах принимает одинаковые значения:
Тогда удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка , в которой производная функции равна нулю:
Следствие 1. В частном случае, когда , из теоремы Лагранжа вытекает, что существует точка , в которой производная функции равна нулю: . Это означает, что теорема Лагранжа является обобщением теоремы Ролля.
Следствие 2. Если во всех точках некоторого промежутка , то в этом промежутке.
Действительно, пусть и – произвольные точки промежутка и . Применяя теорему Лагранжа к промежутку , получим
Однако во всех точках промежутка . Тогда
Учитывая произвольность точек и , получаем требуемое утверждение.
16. Теорема Коши
Формулировка
Геометрически это можно переформулировать так: если и задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр ), то на любом отрезке такой кривой, заданном параметрами и , найдётся касательный вектор, коллинеарныйвектору перемещения от до .
Доказательство
Для доказательства введём функцию
| | |
Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны . Воспользовавшись упомянутой теоремой, получим, что существует точка , в которой производная функции равна нулю, а равна как раз необходимому числу.
17. Правило Лопиталя
Правило Лопиталя — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и ∞/∞.
Суть правила: предел отношения функций равен пределу отношения их производных.
18. Экстремумы функции одной переменной. Необходимое условие экстремума.
Пусть функция f(x), определенная и непрерывная в промежутке [a,b], не является в нем монотонной. Найдутся такие части [ , ] промежутка [a,b], в которых наибольшее и наименьшее значение достигается функцией во внутренней точке, т.е. между и .
Говорят, что функция f(x) имеет в точке максимум (или минимум), если эту точку можно окружить такой окрестностью (x 0 - ,x 0 + ), содержащейся в промежутке, где задана функция, что для всех её точек выполняется неравенство.
f(x) < f(x 0 )(или f(x)>f(x 0 ))
Иными словами, точка x 0 доставляет функции f(x) максимум (минимум), если значение f(x 0 ) оказывается наибольшим (наименьшим) из значений, принимаемых функцией в некоторой (хотя бы малой) окрестности этой точки. Отметим, что самое определение максимума (минимума) предполагает, что функция задана по обе стороны от точки x 0 .
Если существует такая окрестность, в пределах которой (при x=x 0 ) выполняется строгое неравенство
f(x)
то говорят, что функция имеет в точке x 0 собственный максимум (минимум), в противном случае – несобственный.
Если функция имеет максимумы в точках x 0 и x 1 , то, применяя к промежутку [x 0 ,x 1 ] вторую теорему Вейерштрасса, видим, что наименьшего своего значения в этом промежутке функция достигает в некоторой точке x 2 между x 0 и x 1 и имеет там минимум. Аналогично, между двумя минимумами непременно найдется максимум. В том простейшем (и на практике – важнейшим) случае, когда функция имеет вообще лишь конечное число максимумов и минимумов, они просто чередуются.
Заметим, что для обозначения максимума или минимума существует и объединяющий их термин – экстремум.
Понятия максимум (max f(x)) и минимум (min f(x)) являются локальными свойствами функции и имеют место в определенной точке х 0 . Понятия наибольшего (sup f(x)) и наименьшего (inf f(x)) значений относятся к конечному отрезку [a,b] и являются глобальными свойствами функции на отрезке.
Из рисунка 1 видно, что в точках х 1 и х 3 локальные максимумы, а в точках х 2 и х 4 – локальные минимумы. Однако, наименьшего значения функция достигает в точке х=а, а наибольшего – в точке х=b.
Поставим задачу о разыскании всех значений аргумента, доставляющих функции экстремум. При решении ее основную роль будет играть производная.
Предположим сначала, что для фунции f(x) в промежутке(a,b) существует конечная производная. Если в точке х 0функция имеет экстремум, то, применяя к промежутку (х 0 - ,х 0 + ), о которой была речь выше, теорему Ферма, заключаем, что f (x)=0 этом состоит необходимое условие экстремума. Экстремум следует искать только в тех точках, где производная равна нулю.
Не следует, думать, однако, что каждая точка, в которой производная равна нулю, доставляет функции экстремум : указанное только что необходимое условие неявляется достаточным.
19. Экстремумы функции одной переменной. Достаточное условие экстремума.
Дополним, что точки, где производная равна нулю, называются стационарными ; а точки, где производная не существует называются критическими.
Итак, если точка х 0 есть стационарная точка для функции f(x) или если в этой точке не существует для неё двусторонней конечной производной, то точка х 0 представляется, так сказать лишь “подозрительной” по экстремуму и подлежит дальнейшему испытанию.
Это испытание состоит а проверке достаточных условий для существования экстремума, которые мы сейчас утановим.
Предположим, что в некоторой окрестности (х- ,х+ ) точки х 0 (по крайней мере, для х=х 0 ) существует конечная производная и как слева от х 0 , так и справа от х 0 (в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:
1) f’(x)>0 при х<х 0 и f’(x)<0 при х>х 0 , т. е. производная f’(x) при переходе через точку х 0 меняет знак плюс на минус. В этом случае, в промежутке [х 0 - ,х 0 ] функция f(x) возрастает, a в промежутке [х 0 ,х 0 + ] убывает, так что значение f(x) будет наибольшим в промежутке [х 0 - ,х 0 + ] , т. е. в точке х 0 функция имеет собственный максимум.
2) f’(x)<0 при х<х 0 и f’(x)>0 при х>х 0 , т. е. производная f’(x) при переходе через точку х 0 меняет знак минус на плюс. В этом случае аналогично убеждаемся, что в точке х 0 функция имеет собственный минимум.
3) f’(x)>0 как при х<х 0 так и при х>х 0 либо же f’(x) и слева и справа от х 0 , т. е. при переходе через х 0 , не меняет знака. Тогда функция либо всё время возрастает, либо всё время убывает; в любой юлизости от х 0 с одной стороны найдутся точки х, в которых f(x)
Итак, мы получаем правило для испытания “подозрительного” значения х 0 : подставляя в производную f’(x) сначала х<х 0 , а затем х>х 0 , устанавливаем знак производной вблизи от точки х 0 слева и справа от неё; если при этом производная f’(x) меняет знак плюс на минус , то налицо максимум, если меняет знак с минуса на плюс, то – минимум ; если же знака не меняет, то экстремума вовсе нет.
Это правило полностью решает вопрос в том случае, когда в промежутке (а,b), как это обычно бывает, всего лишь конечное число стационарных точек или точек, где отсутствует конечная производная:
a<х 1 <х 2 <… <х k <х k+1 <… <х n
именно ,тогда прежде всего, в любом промежутке (а,х 1 ), (х 1 ,х 2 ), … ,(х k ,х k+1 ), … ,(х n ,b) существует конечная производная f’(x) и, кроме того, в каждом таком промежутке f’(x) сохраняет постоянный знак.Действинельно, если бы f’(x) меняла знак, например, в промежутке (х k ,х k+1 ) , то по теореме Дарбу, она обращалась бы в нуль в некоторой точке между х k и х k+1 , что невозможно, поскольку все корни производной уже содержатся в ряду точек (3.1).
Последнее замечание бывает полезно в некоторах случаях на практике: знак производной f’(x) во всем промежутке (х k ,х k+1 ) определяется , если вычислить значение (или даже только установить знак) её в одной какой-либо точке этого промежутка.
20. Направление выпуклости графика функции. Достаточное условие выпуклости
графика функции.
Направление выпуклости графика функции.
Опр. 1. График функции имеет на интервале выпуклость, направленную вниз, если он расположен не ниже любой касательной, проведённой на этом интервале.
Опр.2. График функции имеет на интервале выпуклость, направленную вверх, если он расположен не выше любой касательной, проведённой на этом интервале.
Теор.1. (Достаточное условие выпуклости графика функции). Если функция имеет на интервале вторую производную, и () для , то её график имеет на этом интервале выпуклость, направленную вниз (вверх).
Док-во. Пусть, для определённости, на . Пусть с - произвольная точка , докажем, что график функции лежит выше касательной, проведённой к нему в точке . Уравнение касательной: ( - текущая точка касательной).
По формуле Тейлора . Вычитая из этого равенства предыдущее, получим на , т.е. точка графика функции действительно лежит выше точки графика касательной.
Аналогично рассматривается случай на .
Достаточное условие вогнутости ( выпуклости ) функции.
Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:
если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );
если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .
21. Точки перегиба. Необходимое условие существования перегиба. Достаточное
условие существования перегиба.
Точка перегиба функции это точка ,в которой существует касательная к графику и существует такая окрестность точки , в которой график имеет разные направления выпуклости.
Необходимые условия наличия перегиба
либо не существует.
Достаточные условия наличия перегиба
1. Если меняет знак при переходе через точку x0, то x0 - точка перегиба.
2. Если то при n четном x0 - точка перегиба, при n нечетном x0 не является точкой перегиба.
22. Понятие о многочлене Тейлора. Формула Тейлора для функции одной переменной (без доказательства). Формула Маклорена для функций , , .
Рассмотрим многочлен -й степени
Его можно представить в виде суммы степеней , взятых с некоторыми коэффициентами. Продифференцируем его раз по переменной , а затем найдем значения многочлена и его производных в точке :
Таким образом, получаем, что
Полученное выражение называется формулой Маклорена для многочлена степени .
Рассуждая аналогично, можно разложить многочлен по степеням разности , где - любое число. В этом случае будем иметь:
Это выражение называется формулой Тейлора для многочлена в окрестности точки .
Разложение функции ex
Так как (ex)' = ex, то производная любого порядка функции ex равна ex. При x = 0 функцияex и ее производные любого порядка равны одному. Таким образом, формула Маклорена для функции ex имеет вид
Отметим, что для любого вещественного числа x остаточный член
В самом деле, если x – фиксированное число, то, начиная с некоторого положительного целого числа N, для любого n > N имеем
Следовательно
так как q < 1, а величина является постоянной при любом n. Таким образом, значения функции ex могут быть найдены приближенно по формуле:
Разложение функции cos x
Находим последовательно производные от f(x) = cos x.
При x = 0 получаем
Следовательно, формула Маклорена для функции cos x имеет вид
Так как , то
для любого фиксированного вещественного числа x. Таким образом, значения функции cosx могут быть найдены приближенно по формуле
Разложение функции sin x
Формула Маклорена для функции sin x находится аналогично формуле Маклорена для cos x
Причем
для любого фиксированного вещественного числа x.
23. Первообразная и неопределенный интеграл. Их свойства.
П. 1. Первообразная и неопределенный интеграл
Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции
F'(x) = f(x).
Обозначение
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.
П.2. Свойства неопределенного интеграла
1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.
24. Первообразная и неопределенный интеграл. Методы вычисления
неопределенных интегралов: интегрирование по частям и замена переменной.
Методы интегрирования.