теория вероятности. 1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы
 Скачать 1.11 Mb.
|
|
20. Статистическая проверка гипотез. Основные понятия. Статистический критерий, ошибки 1-го и 2-го родов, уровень значимости и мощность критерия. Критерий согласия Пирсона. Проверка гипотезы о значении параметров нормального распределения. Проверка гипотезы о законе распределения случайной величины. Статистическая проверка гипотез. Основные понятия. Уровень значимости и мощности критерия Статистической гипотезой наз всякое непротиворечивое множество утверждений 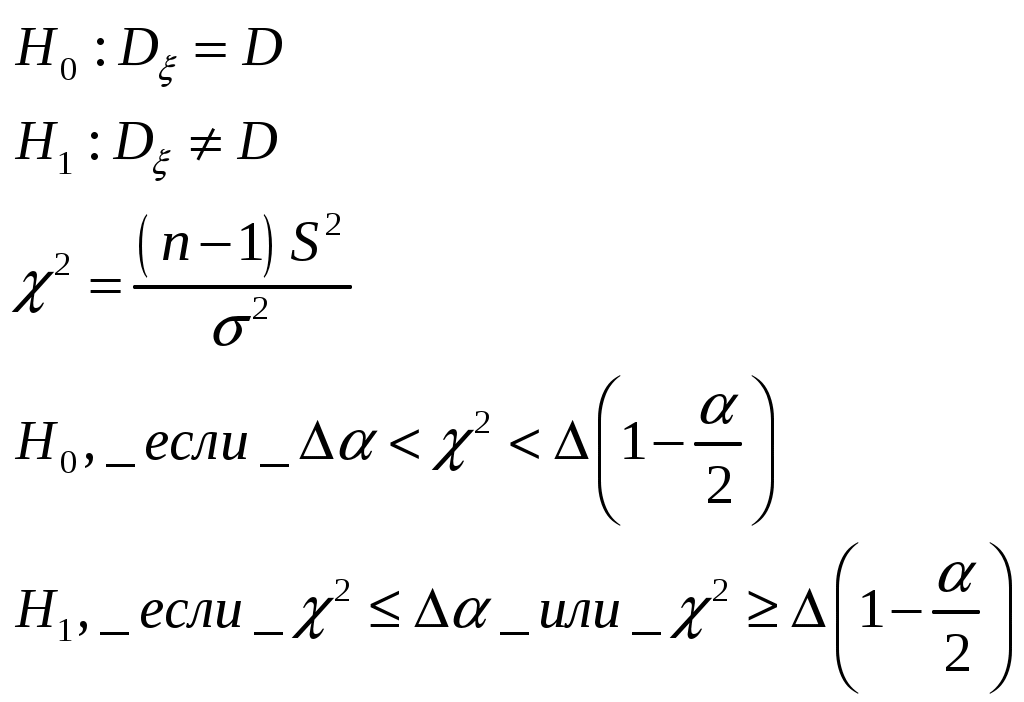 относительно закона распределения случайной величины. С  татистикой нзв произвольная функция Z = φ(Zn) выборки Zn, для значений к-рой известны условные плотности распределения f(z|H0) и f(z|H1) относительно проверяемой гипотезы H0 и конкурирующей с ней альтернативной гипотезы H1. Из опред следует, что Z есть СВ. Практическое применение мат. статистики состоит в проверке соответствия результатов экспериментов предполагаемой гипотезе. С этой целью строится процедура (правило) проверки гипотезы. Критерием согласия называется правило, в соответствии с которым по реализации статистики Z, вычисленной на основании апостериорной выборки zn, гипотеза H0 принимается или отвергается. Критической областью G называется область реализаций z статистики Z, при которых гипотеза H0 отвергается. Доверительной областью G называется область значений z статистики Z, при которых гипотеза H0 принимается. Уровнем значимости α критерия согласия называется вероятность события, стоящего в том, что гипотеза H0 отвергается, когда она верна, т.е.α =P{ZG|H0} где вероятность P соответствует условной плотности распределения f(z|H0). Мощностью γ критерия согласия называется вероятность события, состоящего в том, что гипотеза H0 отвергается, когда она неверна, т.е. γ=P{ZG|H1} где вероятность P соответствует условной плотности f(z|H1). Критической точкой zβ называется точка на оси Oz, являющаяся квантилем уровня β=1 – α распределения F(z|H0), соответствующего плотности распределения f(z|H0). На рис. показана графическая интерпретация введенных понятий, где β + α = 1, δ + γ = 1.  Статистический критерий, ошибки 1-го и 2-го родов Ошибка 1-го рода состоит в отклонении гипотезы, если она верна (пропуск цели). Вероятность совершения ошибки 1-го рода обозначается α и наз. Уровнем значимости. Ошибка 2-го рода – гипотеза принимается, если она неверна – β (ложное срабатывание). Вероятность не совершить ошибку 2-го рода (1-β) наз. ложностью критерия. Критерием (статистическим критерием) наз. случайная величина 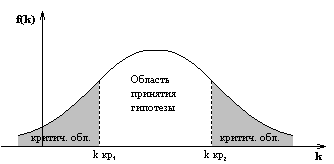 , которая позволяет принять или отклонить нулевую гипотезу. Проверка гипотез о законе распределения случайной величины. Критерий согласия Пирсона. Пусть имеется апостериорная выборка zn и требуется проверить гипотезу H0, состоящую в том, что непрерывная СВ X имеет определенный закон распределения f(x) (например, нормальный, равномерный и т.д.). Истинный закон распределения f(x) неизвестен. Для проверки такой гипотезы обычно используют критерий согласия хи-квадрат χ² (критерий Пирсона). 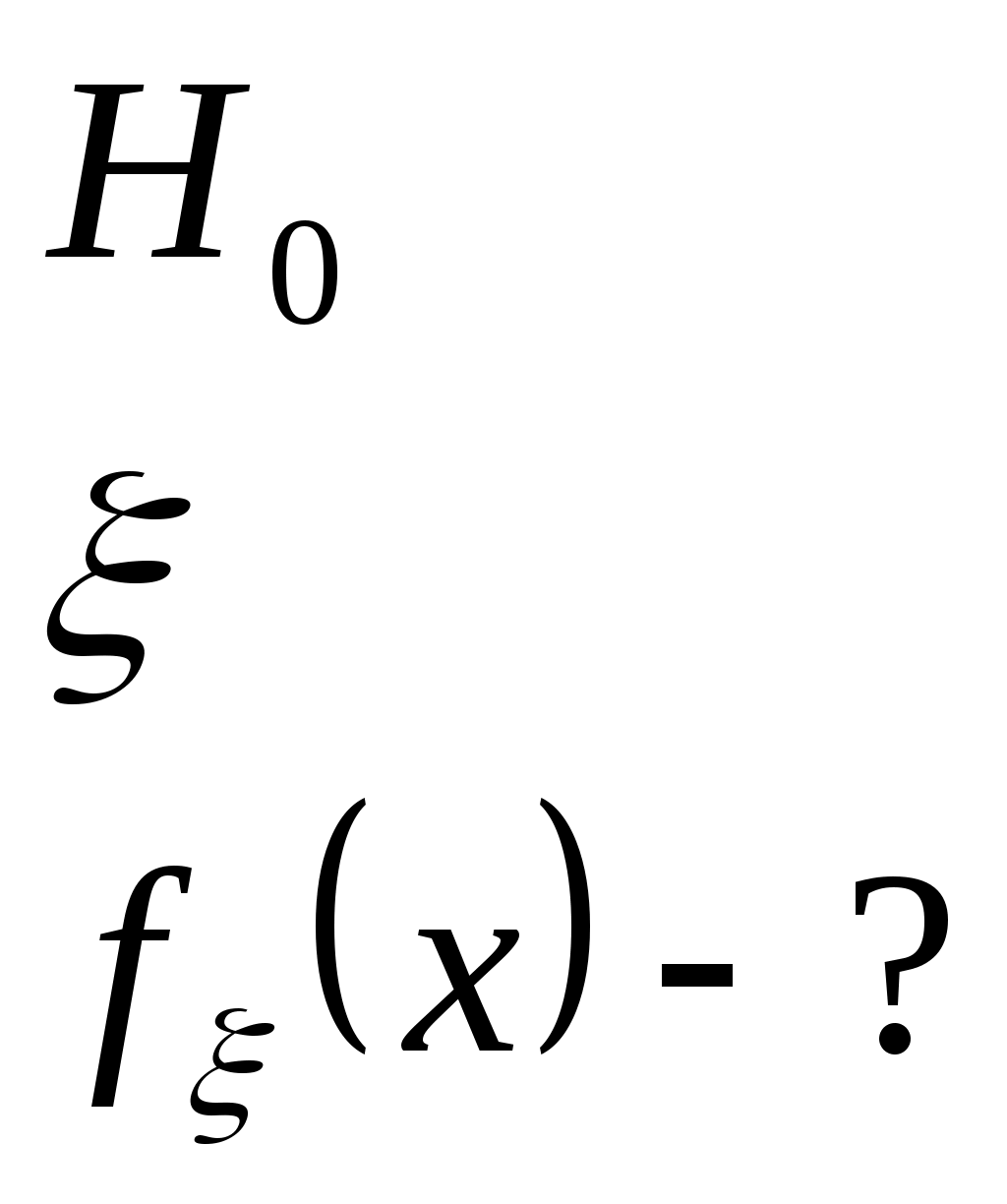  Критерием согласия называется критерий, использованный для проверки гипотез о предполагаемом законе распределения. Проверка состоит в следующем: 1)Строится интервал - статистический ряд и гистограмма 2) По виду гистограммы  3) На основе выборки находим точечные оценки 4) Интервал возможных значений разбиваем на m непересекаемых интервалов. В каждом из них фиксируем число показаний  5) Вычисляем вероятность показаний ξ в каждом интервале 6) Строим критерий χ²  Аналитическое выражение плотности ²- сложное, поэтому задаем уровень значимости α; k; находим 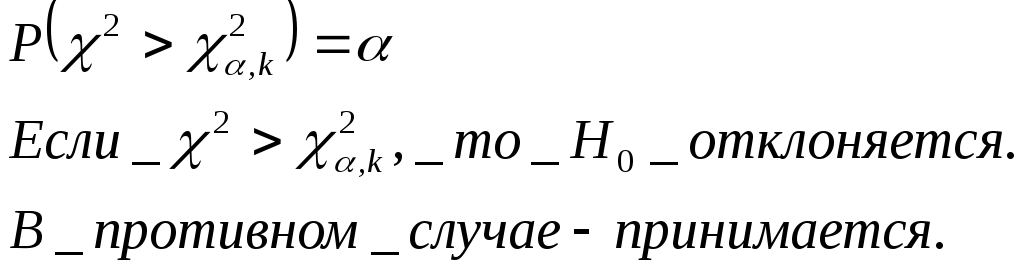   Проверка гипотезы о значении параметров нормального распределения. Пусть известно, что СВ X имеет нормальное распределение. Требуется проверить гипотезу H0, состоящую в том, что mX = m (m - некоторое фиксированное число), используя апостериорную выборку zn. Возможны два случая: дисперсия (σX)2 известна или неизвестна. 1) Дисперсия известна 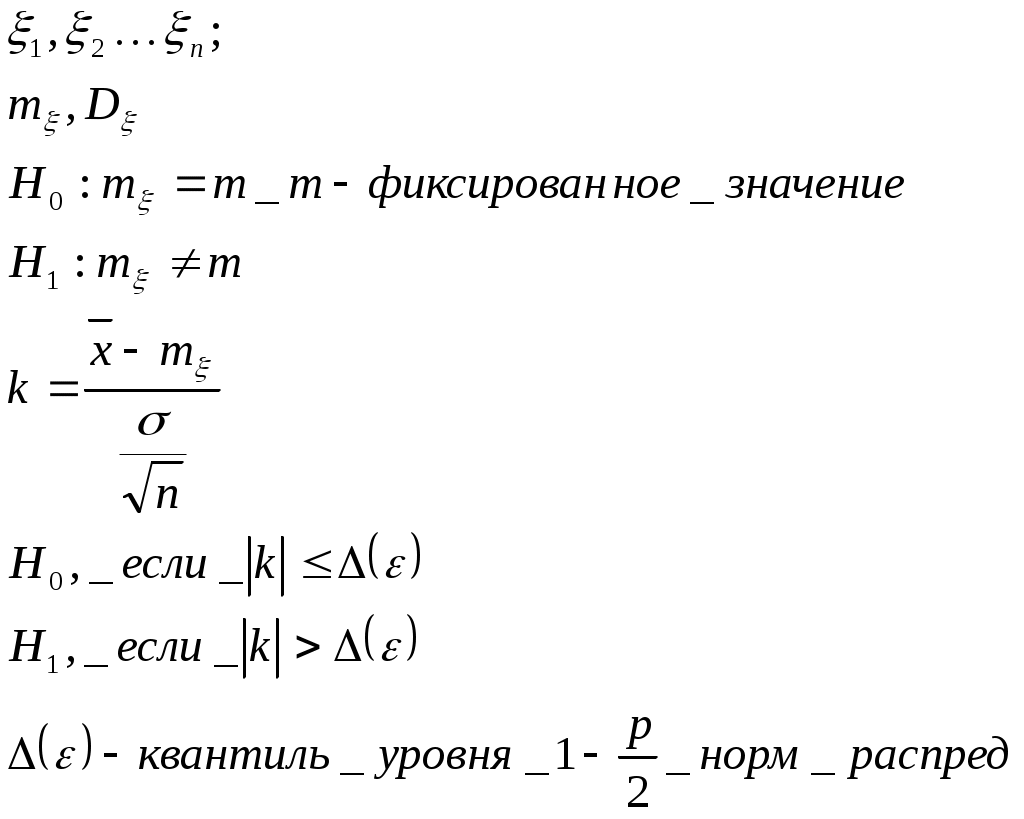 2) Дисперсия неизвестна В качестве оценки вводим выборочную дисперсию В качестве статистики: 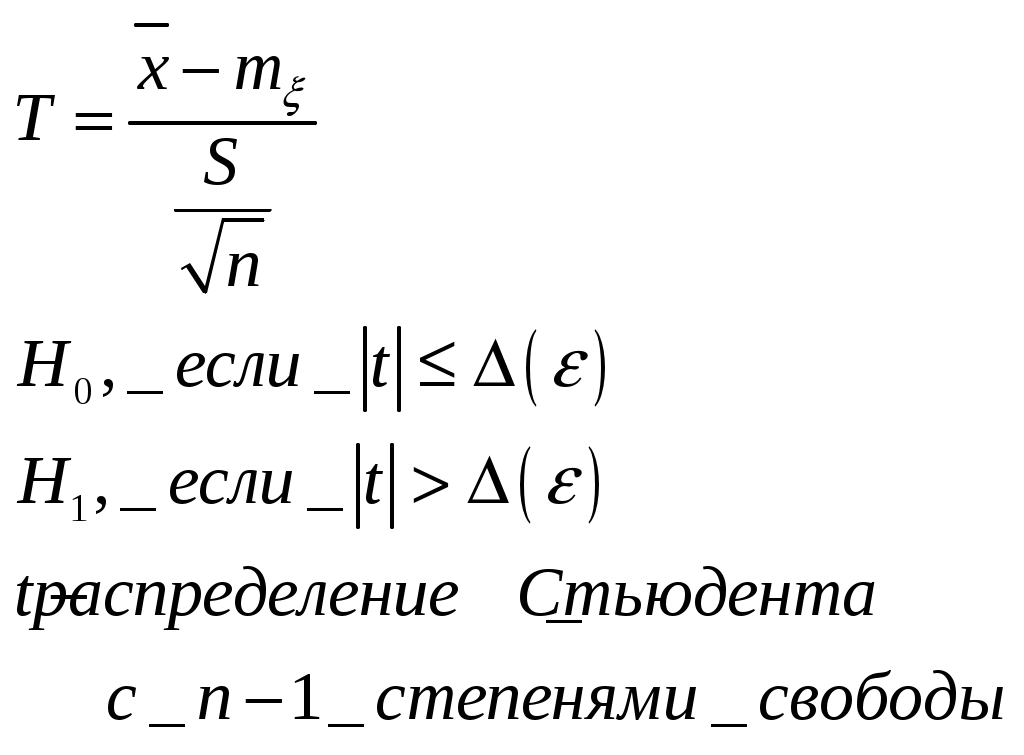 Гипотезы о значении дисперсии |