теория вероятности. 1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы

• Название: 1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы
• Дата: 23.04.2022
• Размер: 1.11 Mb.
• Имя файла: теория вероятности.doc
• Тип: Документы; #492247
• страница: 3 из 5

Теорема. Для того, чтобы случ.вел-ны ξ и  были независимыми, необходимо и достаточно, чтобы ф-ция распред.системы (ξ, η) была равна произведению ф-ций распределения составляющих



Следствие. Для того, чтобы непрерывные случайные величины ξ и  были независимыми, необходимо и достаточно, чтобы плотность совмест.распред.системы (ξ, η) была равна произведению плотностей распред.составляющих:


(9.) Критерии независимости:

1) для всех х,у

2) Непрерывность



3) Дискретность

для всех х, у

Если хотя бы один из критериев не выполняется в любой одной точке, то величины ξ и η зависимы.
15. Условные распределения двумерной случайной величины. Функция распределения и её свойства. Условная плотность распределения и её свойства. Условные числовые характеристики. Корреляционные зависимости. Нормальный закон распределения двумерной случайной величины.

Случайные величины: ξ x_i i=1÷n; η y_j j=1÷m.

Условной функцией распределения случайной величины ξ, при условии, что случайная величина η приняла значение y_i называется условная вероятность.



Свойства условной ф-ции распределения:

1) Fξ(x|y) – определена для всех х

2) Fξ(x|y)  [0,1] для всех х  R

3) Fξ(-∞|y)=0

4) Fξ(+∞|y)=1

5) Сумма вероятностей распределения равна 1.

Имеем y_i:

Имеем x_i:

Используют для контрольного вычисления.
Условная плотность распределения и её свойства

Условной плотностью распределения f_ξ(x/y) непрерывной случайной величины ξ при фиксированном значении η=у называется отношение плтности совместного распределения f_ξη(x/y) случайной величины (ξ,η) к плотности распределения случайной величины ξ.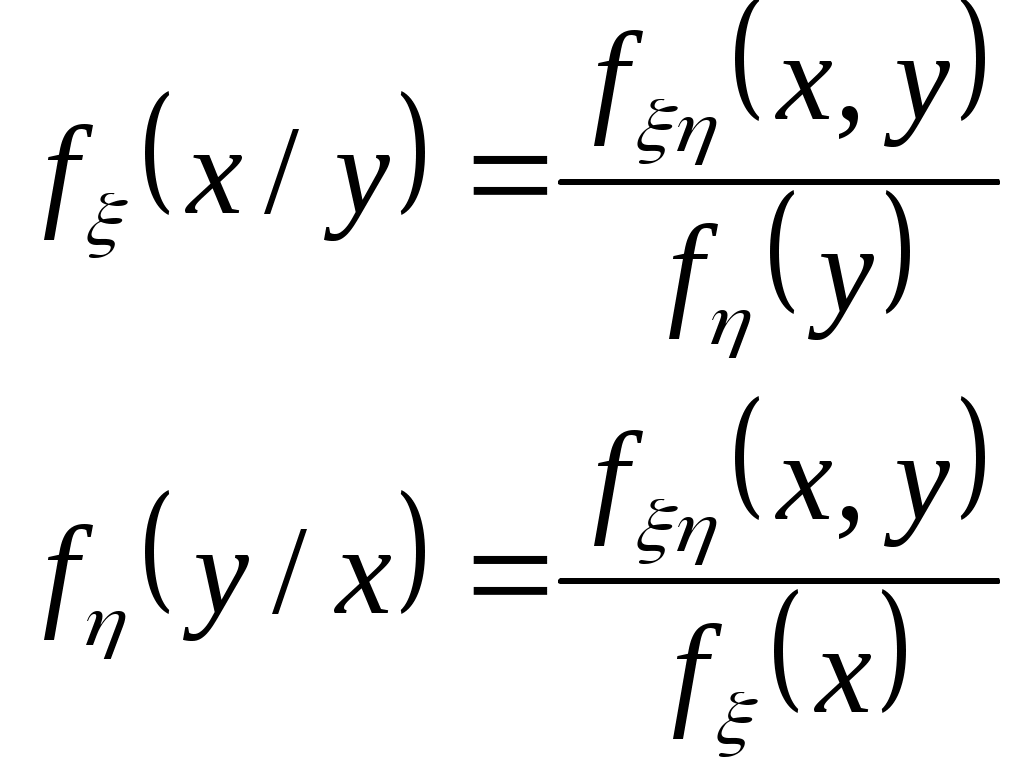



Свойства:

1) f_ξ(x/y)≥0

2)

f_ξ(x/y) – непрерывная функция

3)

4) ξ и η – независимы



5)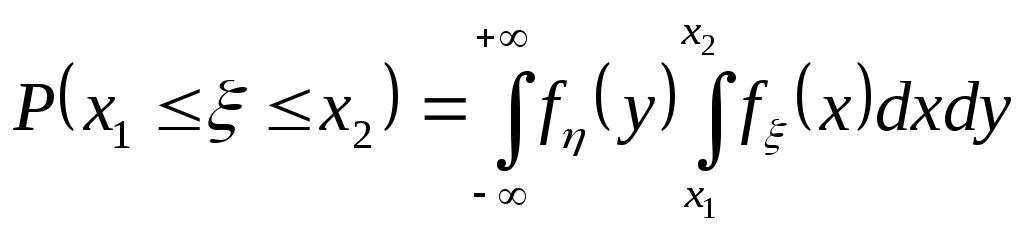
Условные числовые характеристики

Условным мат ожиданием случайной величины ξ называют её мат ожидание, вычисленное при условии, что случайная величина η приняла значение у.



Условное мат ожидание M[ξ|y] случайной величины ξ как функция параметра у называется регрессией ξ на у



Смешанный начальный момента порядка K+S равен мат ожиданию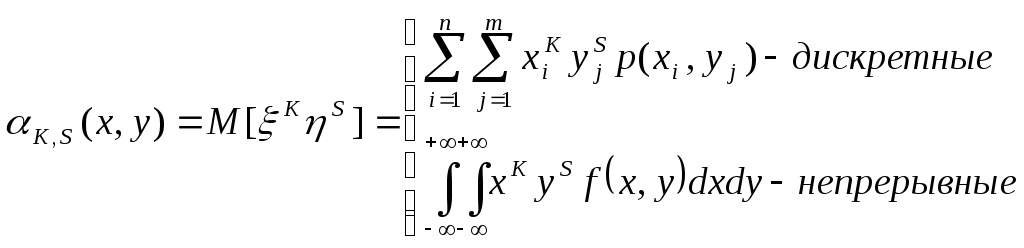



Смешанные центральный момент K+S равен мат ожиданию произведения центрированных величин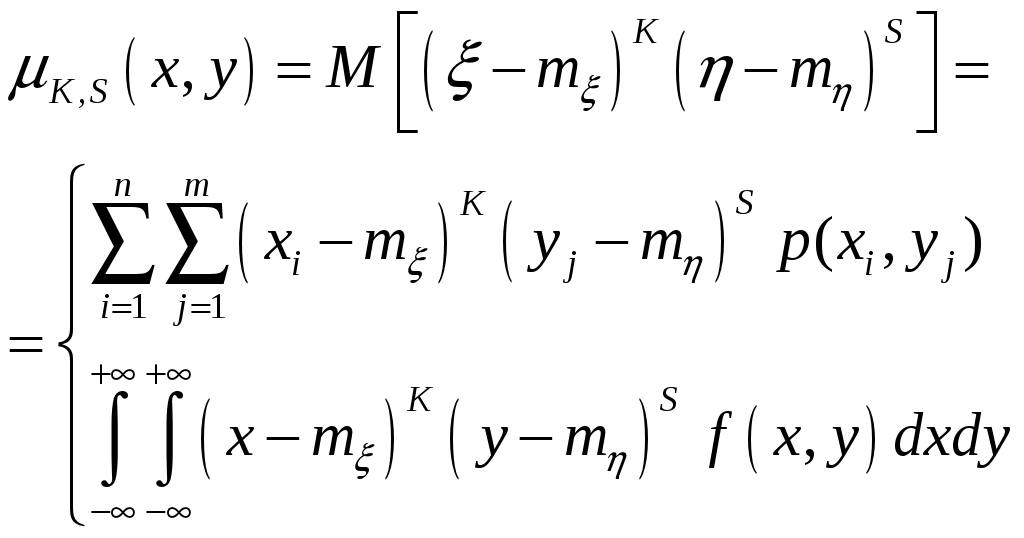



Следствия: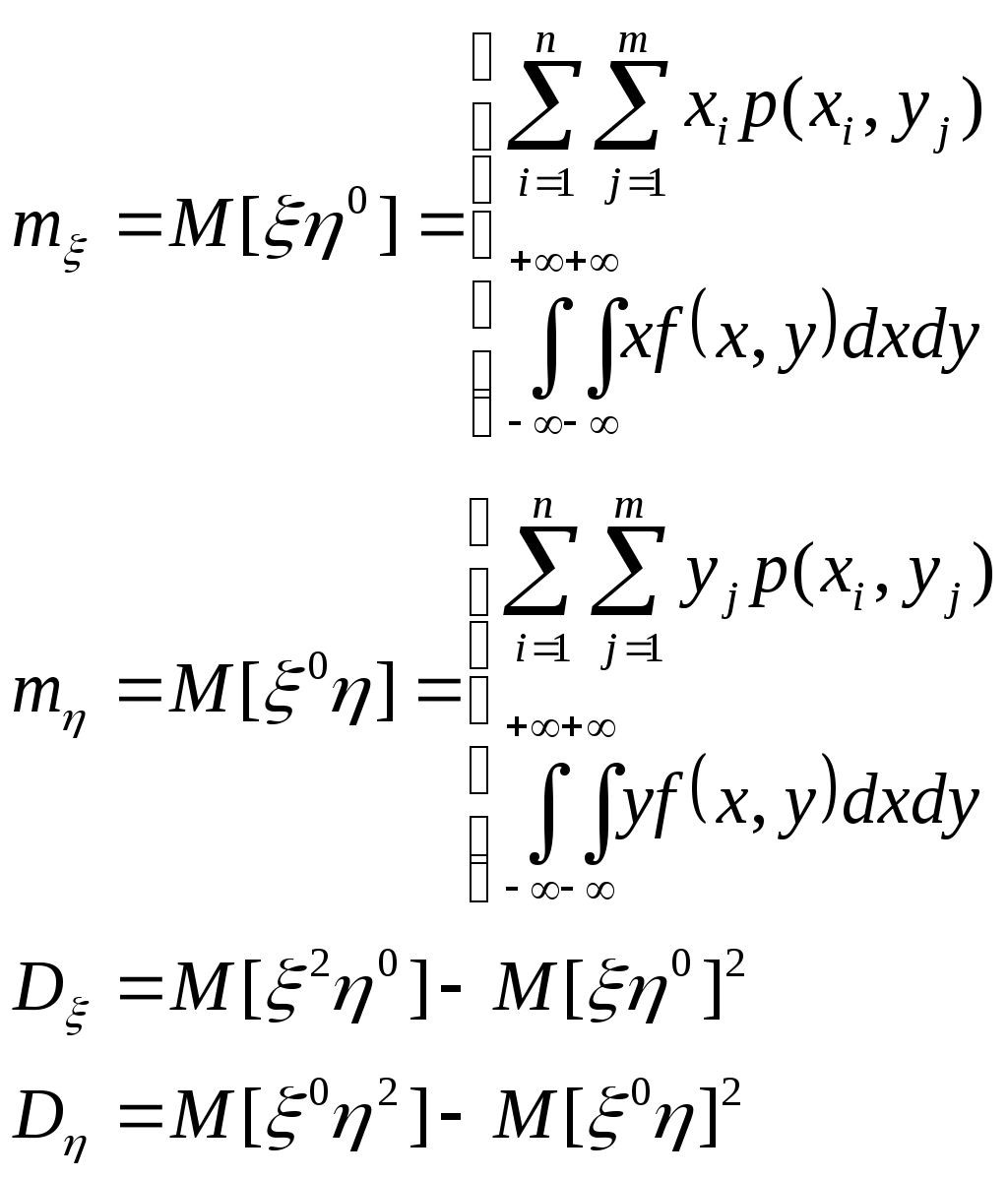


Корреляционные зависимости

Корреляционным моментом (k_ξη) случайных величин ξ и η называют мат ожидание произведения отклонения этих величин от их мат ожидания:

Характеризует степень тесноты линейных величин ξ и η и их рассеивание их значений относительно точки

Свойства:

1) k_ξη = k_ηξ

2) Корреляционный момент двух независимых случайных величин ξ и η равен 0.

3)Абсолютная величина корреляционного момента двух случайных величин ξ и η не превышает среднего геометрического их дисперсий:
Если k_ξη<0, то между ξ и η существует отрицательная корреляционная зависимость(если одно значение растет, то другое значение уменьшается).

Если k_ξη >0, то между ξ и η существует положительная корреляционная зависимость(если одно значение растет, то и другое значение растет).
Коэффициент корреляции (r_ξη) случайных величин ξ и η называется отношение корреляционного момента к произведению среднего квадратических отклонений этих величин:

-1≤ r_ξη ≤1

Две случайные величины ξ и η называются коррелированными, если их корреляционный момент отличен от нуля.

Соответственно, ξ и η называются некоррелированными, если их корреляционный момент равен нулю.
r_ξη=1; ξ и η; η=аξ+b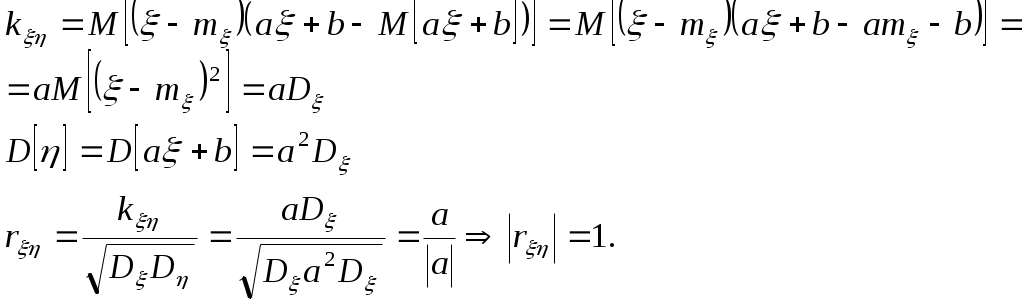


Нормальный закон распределения двумерной случайной величины

Непрерывная двумерная случайная величина (ξ,η) имеет нормальное распределение, если её плотность вероятности равна: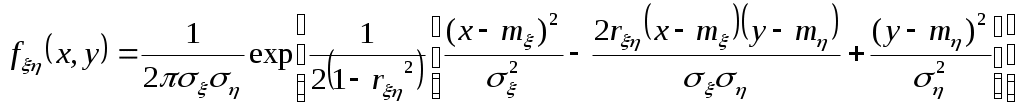



Параметрами нормального закона распределения являются:



Если случайные величины распределены нормально, но они некоррелированны, то r_ξη=0, и получим: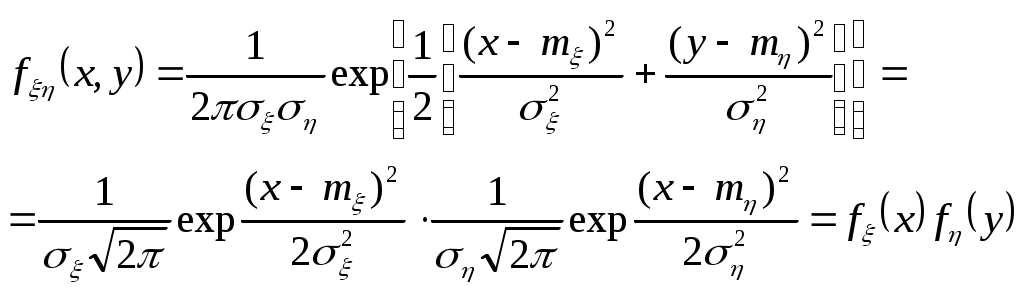



Таким образом, если составляющие нормального распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих.
16. Многомерные случайные величины.Основные характеристики (Ф-я распределения, плотность распр-я, понятие независимости). Основные числовые характеристики (мат.ожидание, дисперсия, корреляционная матрица, коэф-т корреляции, нормированная корреляционная матрица).

Опр. Совокупность произвольного числа n одномерных случ. вел-н , кот. принимают значения одного и того же опыта наз. n-мерной случ. величиной: .

Опр. Ф-я распределения n-мерной случ. величины наз. вероятность выполнения n-неравенств вида:



Опр. Плотность распред-я n-мерной случ. величины наз. смешанная частная производная функции распределения F(х₁,х₂,…,х_n), взятая один раз по каждому аргументу. .

Св-ва плотности рапр-я:

1. f(x₁,x₂,…,x_n) 0

2.

3. Плотности распределения меньшего порядка могут быть получены путем интегрирования n-мерной плотности распр-я по ненужным переменным.



4. Вер-ть попадания многомер.случ.величины в n-мерную область D=n-кратному интегралу по этой области.



Опр. Случайные величины наз. независимыми, если закон распред. каждой частной системы, выделенной из системы не зависит от того, какие значения приняли остальные величины.

f(x₁,x₂,…,x_n)=f₁(x₁)f₂(x₂)…f_n(x_n)
Основные числовые характеристики.

1. Вектор мат. ожидания.

M=(m₁,m₂,…,m_n)



2. Вектор дисперсии.

D=(D₁,D₂,…,D_n)



3. Корреляционная матрица.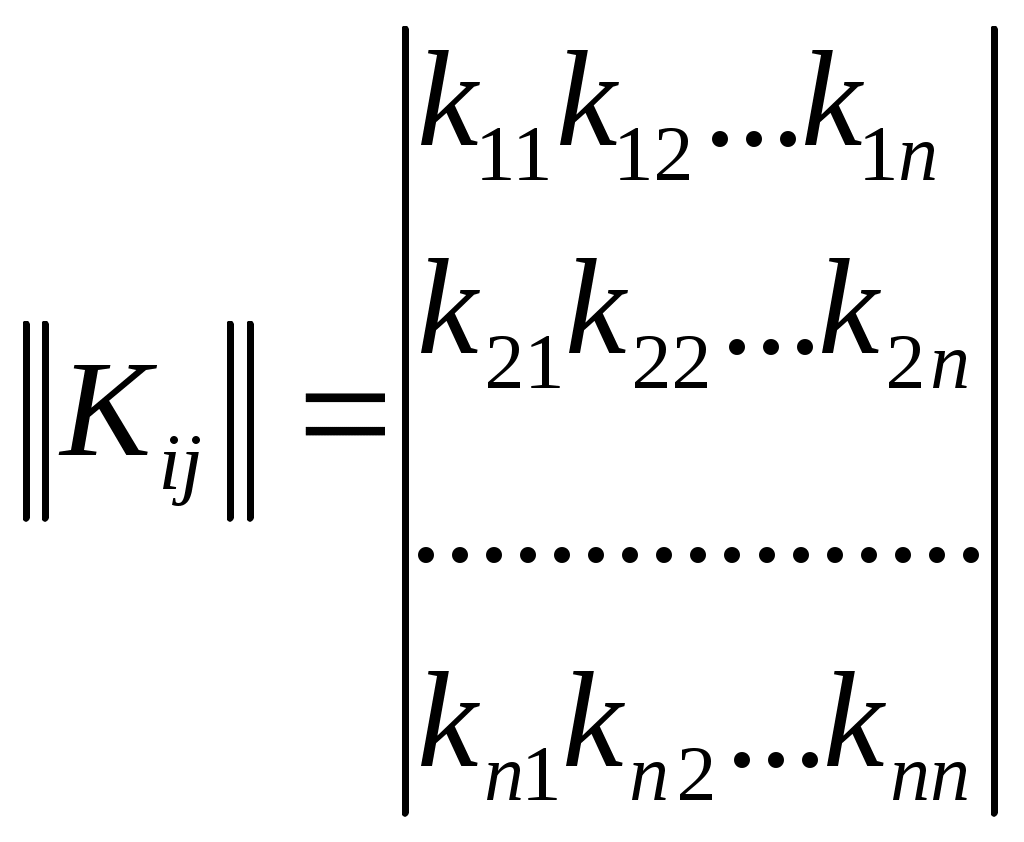



где k_ij=k_ji - т.е. матрица симметрична.





Замечание: случ. величины – будут некоррелированные, если их недиагональные элементы корреляц-ой матрицы=0.

4. Коэф-т корреляции.



5. Корреляционная нормированная матрица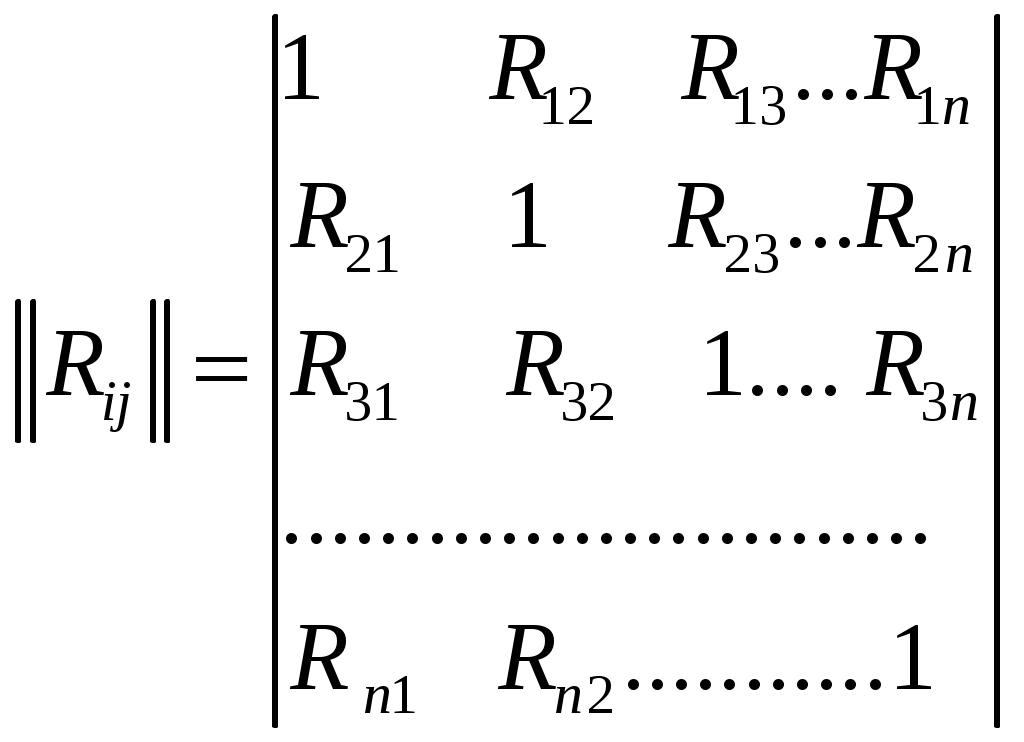

R_ij=R_ji

Случ. величины - независимы, если , где F – ф-ция распред.случ величины.

! Если случ. величины независимы, то они некоррелируемы, НО обратное утверждение НЕВЕРНО!
Коэффициентом корреляции (r_ξη) случ вел ξ и η наз.отношение корреляц.момента к произведению среднеквадратич.отклонений этих величин



-1≤ r_ξη ≤1
17. Основные задачи математической статистики. Генеральная и выборочная совокупность. Повторная и бесповторная выборка. Репрезентативность выборки. Теоретическая ФР. Статистическое распределение выборки. Эмпирическая функция распределения. Гистограмма, полигон относительных частот. Статистические оценки параметров распределения (выборочная, средняя, групповая и общая средняя, выборочная дисперсия). Формула для вычисления дисперсии.

Статистика разрабатывает методы сбора данных и группировки по умолчанию. Задачи мат стат.: 1) указать способы сбора и группировки стат. сведений, полученных в рез-те наблюдения за случ. процессами; 2) разработка методов анализа стат. данных в зависимости от цели исследования.

Генеральная и выборочная совокупность:

Генеральной совокупностью опыта наз. множ-во объектов, из к-ых производится выборка. Выборочной совокупностью или просто выборкой наз. совокупность случайно отобранных объектов.

{х₁, х₂, …, х_n} n-объём выборки

Объёмом совокупности (выборочной или генеральной) наз. число объектов этой совокупности.

Повторная и бесповторная выборка. Репрезентативность выборки. Теоретическая ФР.

Повторной наз.выборку, при к-ой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной наз.выборку, при к-ой отобранный объект в генеральную совокупность не возвращается. Выборка будет репрезентативной, если её осуществлять случайно, то есть каждый из объектов генеральной совокупности имеет одинаковую вероятность попасть в выборку.

k-кол-во выборок, которые можно сделать

n-объём выборки

:



…………………



Пусть F_ξ(x) – функция распределения, тогда каждую из следующих выборок:

, …..

можно рассмотреть как реализацию n-мерной случайной величины (ξ₁, ξ₂,…, ξ_n) Для всех ξ_i закон распределения единственный. Все компоненты (ξ_i) – независимы.

Тогда F(х₁,х₂,…,х_n)=F(x₁)F(x₂)…F(x_n)

Вариационным рядом наз.выборка полученная в рез-те расположения значений исходной выборки в порядке возрастания.

наз. вариантами.

В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности наз. теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том,что теоретическая функция F(x) определяет вер-сть события X*(x)=n_x/n определяет относительную частоту этого же события.

Статистическое распределение выборки:

x₁ – наблюдается n₁ раз

x₂ – n₂

x_k – n_k

xi	x1	x2	……	xk
P*i	n1	n2	……	nk

n_i - частота

-относительная частота



Замечание: В теории вероятности под распределениями понимают соответствие между возможными значениями случ.величины и их вер-тями. А в мат.статистике – соответствие между наблюдаемыми вариантами и их частотами.

Эмпирическая функция распределения:

n_x-число наблюдений, при которых наблюдалось значение признака варианты меньше, чем х

n-общее число наблюдений (объём выборки)


-частота события, когда 
Эмперической функцией распределения случ.величины  наз.функцию F*_ξ(x), определяющую для каждого значения x относительную частоту событий: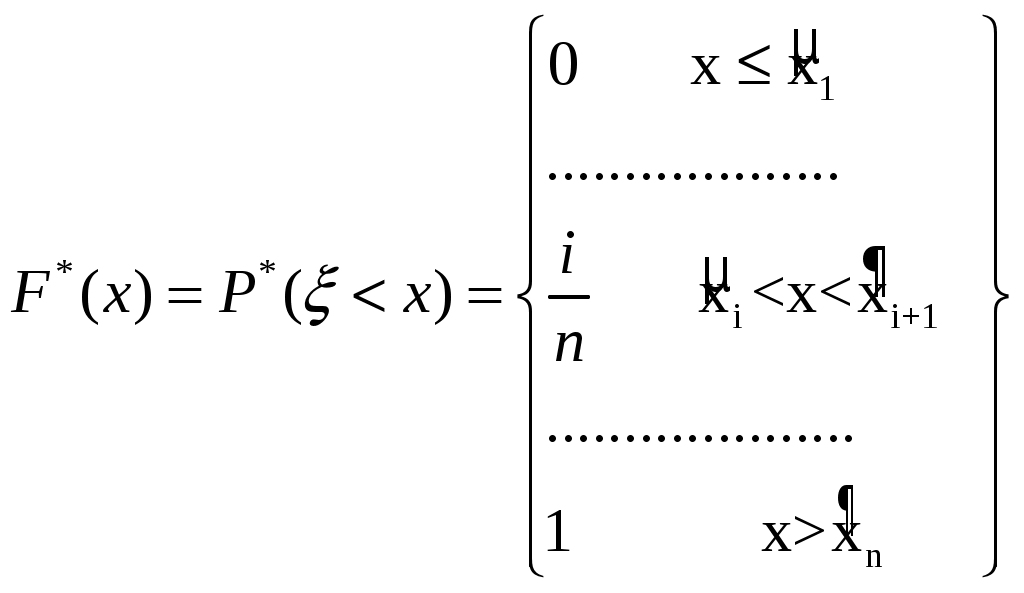







Недостатки:

Невысокая наглядность (визуально сложно определить закон распределения сл.величины )

Гистограмма и полигон относит.частот:

Полигоном частот наз.ломаную, отрезки к-ой соединяют x_i и n_i.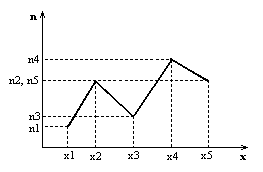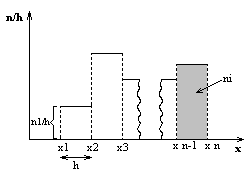



Площадь гистограммы частот =сумме всех частот, то есть объёму выборки.