теория вероятности. 1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы
 Скачать 1.11 Mb.
|
|
Статистические оценки параметров распределения (выборочная средняя, групповая и общая средняя, выборочная дисперсия). Формула для вычисления дисперсии. *-статистическая оценка  xi -значение выборки 1) Оценка параметра наз.состоятельной, если при увеличении объёма выборки n она сходится по вероятности к значению теоретической оценки . Состоятельность -минимальное требование к оценкам.  2) Оценка * наз.несмещённой, если её мат.ожидание равно параметру для любого объёма выборки  3) Смещённой наз. оценку, мат.ожидание к-ой не равно оцениваемому параметру. 4) Несмещённая оценка * наз.эффективной, если её дисперсия минимальна по отношению к дисперсии любой другой оценки этого параметра  Выборочная средняя: Выборочной средней  наз.среднее арифметическое значений признака выборочной совокупности.1) х1,х2,…,хn -все различны n-объём выборки  2) х1,х2,…,хk -появляются с опред.частотой. x1 – появляется n1 раз x2 – n2 xk – nk  Групповая и общая средняя: Групповой средней наз.среднее арифметическое значений признака, принадлежащих группе. Общей средней наз.среднее арифм.значений признака,принадлежащих всей совокупности(выборки) -  Выборочная дисперсия (Dв): Выборочной дисперсией наз.среднее арифмет.квадратов отклонения наблюдаемых значений признака от их среднего значения. 1)  2)  Среднеквадратическое отклонение. Формула дисперсии.  Выборочная дисперсия=ср.арифметическому квадрату значений выборки между квадратом общей средней. 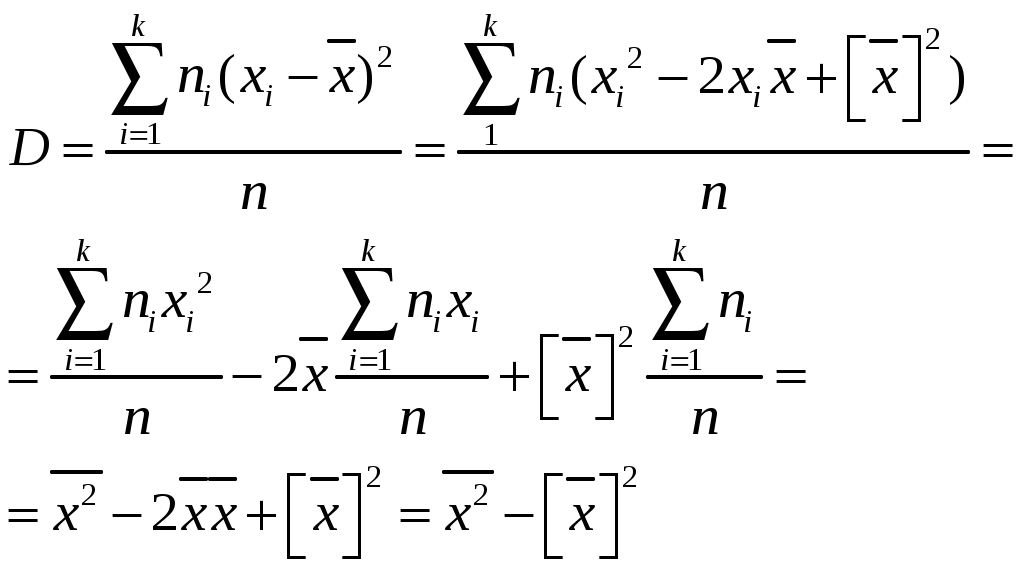  18. Основные распределения в статистике. Распределение хи-квадрат. Распределение Стьюдента. Распределение Фишера. Распределение ² Пусть независимые случ.величины ξi где  распределены по нормальному закону распределения, причем M[ξi]=0, а средн.квадратич. отклонение=1, тогда величина ξi распределена по закону ² с n степенями свободы. ξi распределено по норм.закону-это значит,что: 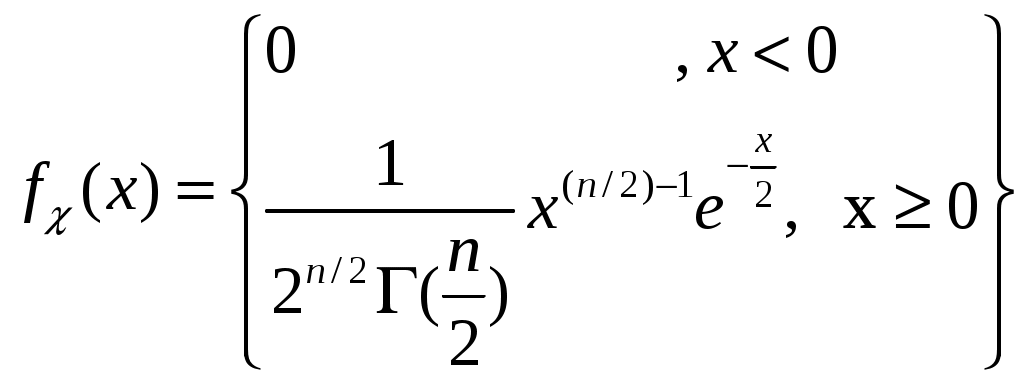    -гамма функция m-положительна Г(m+1)=Г(m) m-целое Г(m)=(m-1)! Распределение ² опред.одним параметром - числом степеней свободы n f(x) - называется графиком Пирснона Они ассиметричны и начинаются с n>2, имею один максимум в значении x=n-2 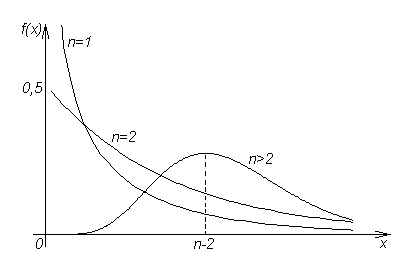 Характериситческая ф-ция 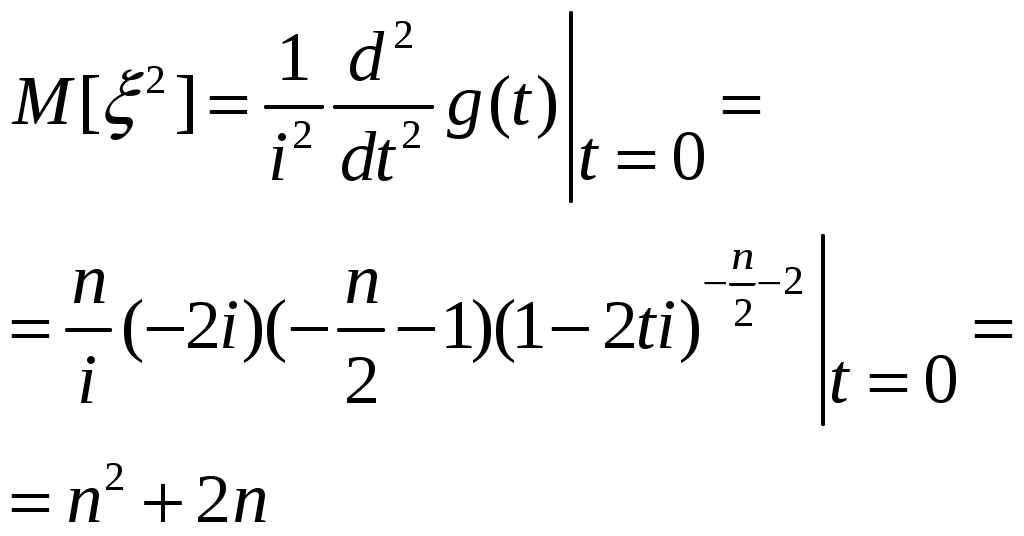    Распределение Стьюдента: Пусть V не зависит от Z и V распределена по закону ², и есть n степеней свободы, тогда вводим величину  , тогда величина T имеет распределение Стьюдента t с n-степенями свободы. Плотность распределения:  Графики fT(x) наз.кривыми Стьюдента, симметрична при всех n = 1,2,... относительно оси ординат.   С возрастанием числа степеней свободы распр-е Стьюдента быстро приближается к нормальному. Распределение Фишера:  -независимые случ.величины, распределены по нормальному закону ² с n и m степенями свободы, тогда  распределение Фишера с n и m степенями свободы. Плотность этого распределения:  где  Распределение Фишера определяется 2-мя параметрами – числами степеней свободы. 19. Статистические оценки. Точечные оценки. Метод максимального правдоподобия. Метод наименьших квадратов. Интервальные оценки. Стат.оценкой неизвестного параметра теоретического распределения нзв ф-цию от наблюдаемых случайных величин. Несмещенной нзв стат.оценку, мат.ожид.к-рой равно оцениваемому параметру при любом объеме выборки, т.е. M[*]=. Смещенной нзв оценку, мат.ожид.к-рой не равно оцениваемому параметру. Эффективной нзв оценку, к-рая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию. С  остоятельной нзв оценку, к-рая при n∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n∞ стремится к 0, то такая оценка оказывается и состоятельной.Точечные оценки Точечной нзв оценку, к-рая опред-ся одним числом, например: генеральная средняя, выборочная средняя, групповая и общая средние, генеральная дисперсия, выборочная дисперсия и др.  xi – значения выборки При выборке малого объема точечная оценка может знач.отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Несмещенной оценкой генеральной средней (мат ожидания) служит выборочная средняя  ,где xi –варианта выборки, ni-частота варианты xi,  -объем выборки.Замечание1.Если первоначальные варианты xi-большие числа,то для упрощения расчета из каждой варианты одно и то же число С,т.е. перейти к условным вариантам ui=xi-C, тогда  .Смещенной оценкой генеральной дисперсии служит выборочная дисперсия  ,эта оценка является смещенной, т к  Замечание2.Если первоначальные варианты xi-большие числа, то целесообразно вычесть из всех вариант одно и то же число C,равное выборочной средней или близкое к ней,т.е. перейти к условным вариантам ui=xi-C (дисперсия при этом не изменится). Тогда  Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями,умножают первоначальные варианты на постоянное число C=10k,т.е. переходят к условным вариантам ui=Cxi . При этом дисперсия увеличится в C2 раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на C2:  Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия  В условных вариантах она имеет вид  Причем если ui=xi-C,то s2x=  ; если ui=Cxi , то s2x= ,то s2x= /C2.Примечание 4. При большом числе данных используют метод произведений или метод сумм. Метод максимального правдоподобия. Метод м.п. точечной оценки неизвестных параметров заданного распределения сводится к отысканию максимума ф-ции одного или нескольких оцениваемых параметров. А) Дискретные случ величины. Пусть Х-дискретная случ величина,кот в результате n опытов приняла возможные значения х1,х2..хn.Допустим,что вид закона распределения случ велич Х задан,но неизвестен параметр ,которым определяется этот закон;требуется найти его точечную оценку *=*( х1,х2..хn). Обозначим вероятность того,что в результате испытания величина Х примет значение хi через p(xn; ). Функцией правдоподобия дискретной случайной величины Х назыв ф-цию аргумента : L(х1,х2..хn; )=p(x1; )* p(x2; )… p(xn; ) . Оценкой наибольшего правдоподобия параметра назыв такое его значение *,при кот ф-ция правдоподобия достигает максимума.Функции L и lnL достигают максимума при одном и том же значении ,поэтому вместо отыскания максимума ф-ции L ищут,что удобнее,максимум ф-ции lnL. Логарифмической ф-цией правдоподобия назыв ф-цию lnL.Точку максимума ф-ции lnL аргумента можно искать,например,так: 1.найти производную  2.приравнять производную 0 и найти критич точку *-корень получ ур-ия (ур-ия правдоподобия) 3.найти вторую производную  ,если вторая производная при =* отрицательна,то *-точка максимума. Найденную точку максимума * принимают в качестве оценки наибольшего правдоподобия параметра .Б) Непрерывные случайные величины. Пусть Х-непрерывн случ велич,которая в результате n испытаний приняла значения х1,х2..хn. Допустим,что вид плотности распределения-ф-ции f(x) – задан,но неизвестен параметр θ,которым определяется эта ф-ция. Ф-ией правдоподобия непрерывной случ величины Х назыв ф-цию аргумента : L(х1,х2..хn; )=f(x1; )* f(x2; )… f(xn; ). Оценку наибольшего правдоподобия неизвестного параметра распределения непрерывной случ величины ищут также,как в случае дискретной случ величины. Если плотность распределения f(x) непрерывной случ величины определяется двумя неизвестными параметрами 1и 2,то ф-ция правдоподобия есть ф-ция двух независ аргументов 1и 2: L= f(x1; 1, 2)* f(x2; 1, 2)… f(xn; 1, 2). Далее находят логарифмическую ф-цию правдоподобия и для отыскания ее максимума составл и решают систему  Метод наименьших квадратов а0, а1,…,an 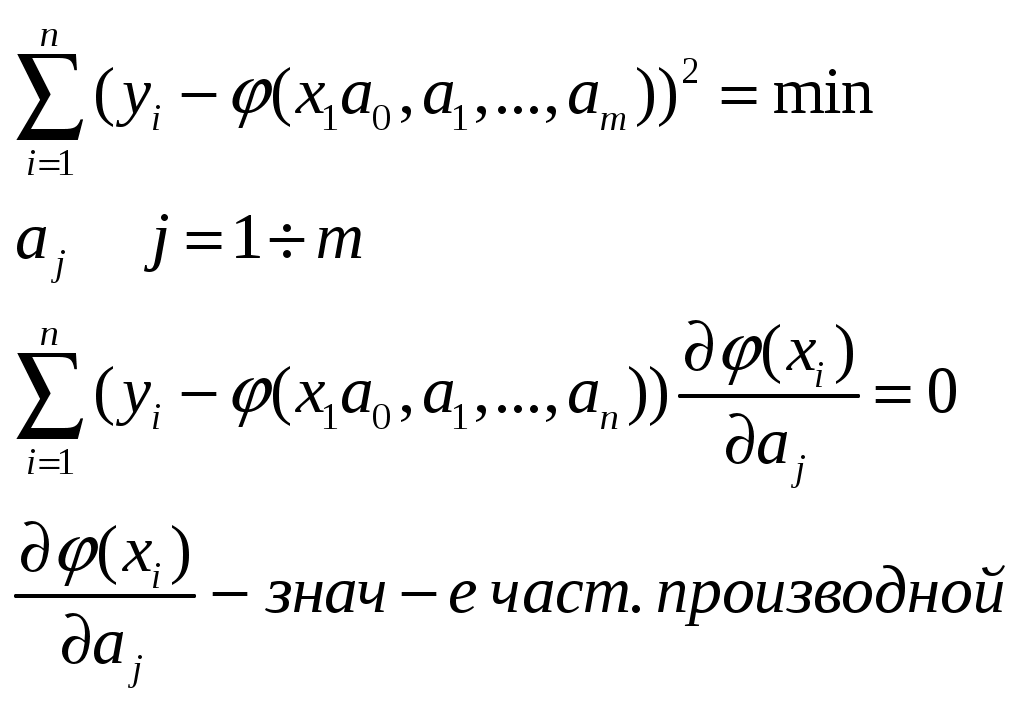 (m+1) уравнений y=ax+b (x1, y1), (x2, y2)… 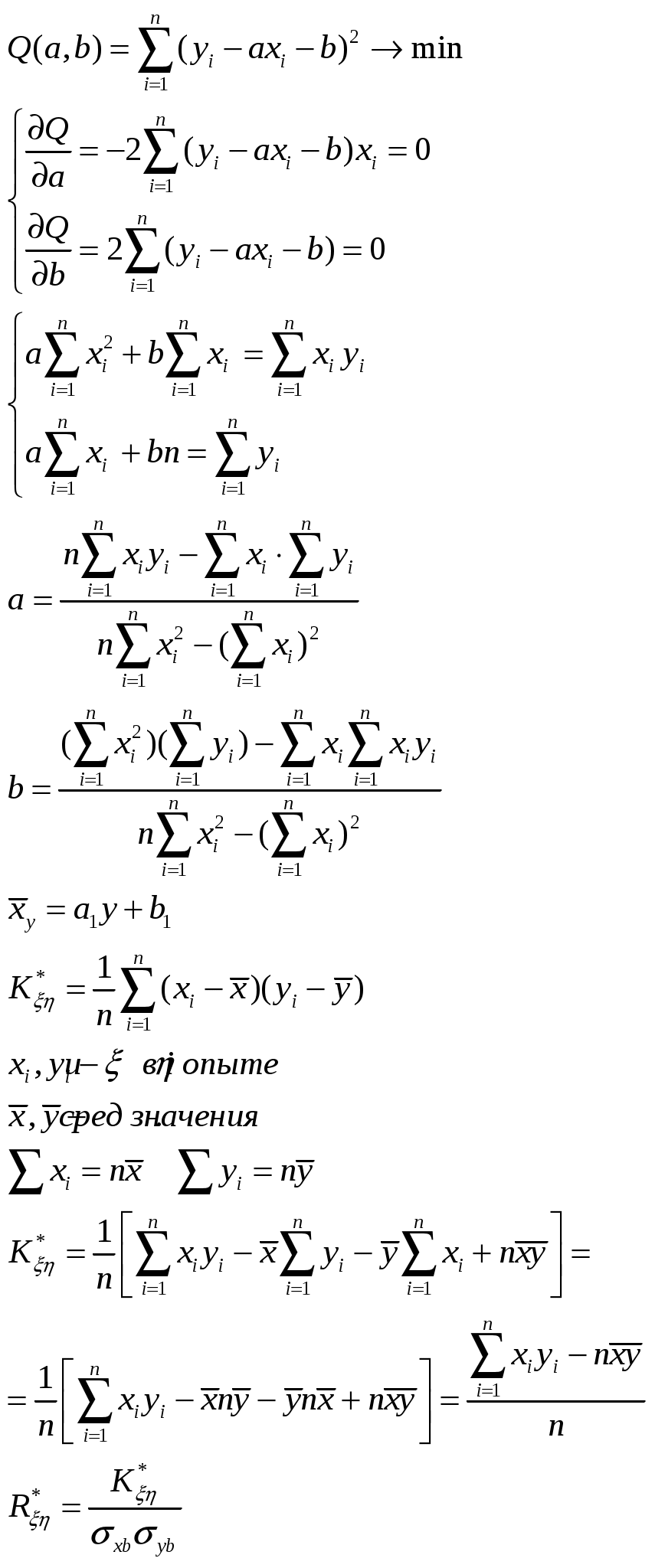 Интервальные оценки Интервальной нзв оценку, к-рая определяется двумя числами – концами интервала. Инт.оценки позволяют установить точность и надежность оценок. Надежностью (доверительной вероятностью) оценки по * нзв вер-ть γ, с к-рой осуществл.нерав-во | - *|<δ. Заменив нерав-во | - *|<δ равносильным ему двойным нерав-вом -δ< - *<δ или *-δ<<δ+* имеем  Доверительным нзв интервал (*-δ, *+δ), к-рый покрывает неизвестный параметр с заданной надежностью γ. 1.Интервальной оценкой (с надежностью γ) математического ожидания а нормально распределенного количественного признака X по выборочной средней  при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал Где  - точность оценки, n-объем выборки, t-значение аргумента ф-ции Лапласа Ф(t),при котором Ф(t)=γ/2; при неизвестном σ (и объеме выборки n<30) где s-«исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице по заданным n и γ. 2. Интервальной оценкой (с надежностью γ) среднего квадратического отклонения σ нормально распределенного количественного признака X по «исправленному» выборочному среднему квадратическому отклонению s служит довер. инт-л  (при q<1) (при q>1)Где q находят по таблице по заданным n и γ 3. Интервальной оценкой (с надежностью γ) неизвестной вер-ти p биноминального распред-я по относ. частоте ω служит довер.инт-л (с приближ. концами p1 и p2)  где   Где n-общее число испытаний; m-число появлений событий; ω-относ.частота, равная отношению m/n;t-значение аргумента ф-ции Лапласа, при к-ром Ф(t)=γ/2(γ-заданная надежность). Замечание. При больших значениях n (порядка сотен) можно принять в кач-ве приближ.границ довер.инт-ла  |