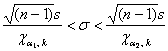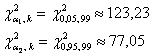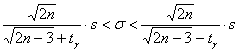|
|
11.05.2023.Пр.р.15.Вычисление интервальной оценки, доверительног. Практическая работа в форме практической подготовки 15
Здравствуйте, ребята. Вот тема на сегодня.
Практическая работа в форме практической подготовки №15. Вычисление интервальной оценки, доверительного интервала, уровня значимости, доверительной вероятности.
Напишите конспект.
Для изучения генеральной совокупности объёма 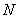 из неё производится выборка, состоящая из из неё производится выборка, состоящая из 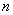 элементов, которая хорошо характеризует всю совокупность. И на основании исследования этой выборочной совокупности с высокой достоверностью можем оценить генеральные характеристики. Чаще всего требуется выявить закон распределения генеральной совокупности и оценить его числовые параметры, такие как генеральная средняя элементов, которая хорошо характеризует всю совокупность. И на основании исследования этой выборочной совокупности с высокой достоверностью можем оценить генеральные характеристики. Чаще всего требуется выявить закон распределения генеральной совокупности и оценить его числовые параметры, такие как генеральная средняя 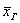 , генеральная дисперсия , генеральная дисперсия 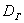 и среднее квадратическое отклонение и среднее квадратическое отклонение 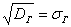 . .
Для оценки этих параметров нужно вычислить соответствующие выборочные значения. Так, выборочная средняя 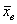 позволяет нам оценить генеральную среднюю позволяет нам оценить генеральную среднюю 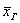 . Несмещённой точечной оценкой генеральной дисперсии . Несмещённой точечной оценкой генеральной дисперсии 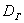 является исправленная выборочная дисперсия является исправленная выборочная дисперсия 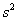 , и стандартного отклонения , и стандартного отклонения 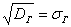 – исправленное стандартное отклонение – исправленное стандартное отклонение 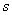 . .
Справка: 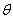 – греческая буква «тета», – греческая буква «тета», 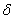 – греческая буква «дельта». – греческая буква «дельта».
Значение 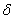 называется точностью оценки, и можно записать с помощью модуля: называется точностью оценки, и можно записать с помощью модуля:
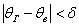
Обозначение: точность оценки также обозначают через 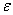 («эпсилон»). («эпсилон»).
Но статистические методы не позволяют 100%-но утверждать, что рассчитанное значение 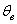 будет удовлетворять этому неравенству – ведь в статистике всегда есть место случайности. Таким образом, можно говорить лишь о вероятности будет удовлетворять этому неравенству – ведь в статистике всегда есть место случайности. Таким образом, можно говорить лишь о вероятности 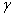 , с которой это неравенство осуществится: , с которой это неравенство осуществится: 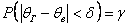 . .
Теперь раскроем модуль:
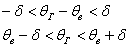
Интервал 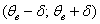 называется доверительным интервалом и представляет собой интервальную оценку генерального значения называется доверительным интервалом и представляет собой интервальную оценку генерального значения 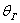 по найденному выборочному значению по найденному выборочному значению 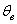 . Данный интервал с вероятностью . Данный интервал с вероятностью 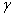 «накрывает» истинное значение «накрывает» истинное значение 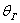 . Эта вероятность называется доверительной вероятностью или надёжностью интервальной оценки . Эта вероятность называется доверительной вероятностью или надёжностью интервальной оценки
Надёжность «гамма» часто задаётся наперёд, популярные варианты 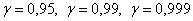
Пример 1
Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением 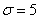 . Найти доверительный интервал для оценки математического ожидания . Найти доверительный интервал для оценки математического ожидания 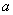 с надежностью 0,95, если выборочная средняя с надежностью 0,95, если выборочная средняя 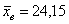 , а объем выборки , а объем выборки 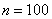 . .
здесь известно стандартное отклонение 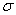 генеральной совокупности. генеральной совокупности.
– из генеральной совокупности попугаев проведена выборка в 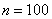 особей и по её результатам найдена выборочная средняя: особей и по её результатам найдена выборочная средняя: 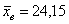 . .
Выборочная средняя – это точечная оценка неизвестной нам генеральной средней 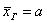 Недостаток точечной оценки состоит в том, что она может оказаться далёкой от истины. И по условию, требуется найти интервал Недостаток точечной оценки состоит в том, что она может оказаться далёкой от истины. И по условию, требуется найти интервал  , которой с вероятностью , которой с вероятностью 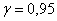 накроет истинное значение накроет истинное значение 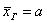 . Здесь будет неверным сказать, что . Здесь будет неверным сказать, что 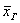 попадёт в этот интервал. попадёт в этот интервал.
Точность оценки рассчитывается по формуле 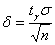 , где , где 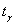 – коэффициент доверия. Этот коэффициент отыскивается из соотношения – коэффициент доверия. Этот коэффициент отыскивается из соотношения 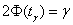 , где , где 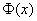 – функция Лапласа. – функция Лапласа.
В данном случае 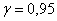 , следовательно: , следовательно:
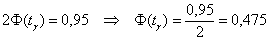
И по таблице значений функции Лапласа либо пользуясь расчётным макетом, выясняем, что значению 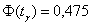 соответствует аргумент соответствует аргумент 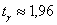 . .
Таким образом, точность оценки:
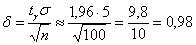
и искомый доверительный интервал:
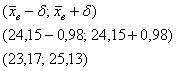
Этот интервал с вероятностью 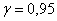 (надёжностью) накрывает истинное генеральное значение (надёжностью) накрывает истинное генеральное значение 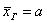 . Но всё же остаётся 5%-ная вероятность, что генеральная средняя окажется вне найденного интервала. . Но всё же остаётся 5%-ная вероятность, что генеральная средняя окажется вне найденного интервала.
Ответ: 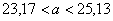 . .
Пример 2
В результате 10 независимых измерений некоторой величины 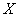 , выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице: , выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице:

Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение величины 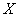 при помощи доверительного интервала, покрывающего это значение с доверительной вероятностью 0,95. при помощи доверительного интервала, покрывающего это значение с доверительной вероятностью 0,95.
Решение следует начать с вычисления выборочных характеристик: 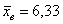 и и 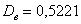 . По условию, требуется оценить генеральную совокупность (а именно, параметр . По условию, требуется оценить генеральную совокупность (а именно, параметр 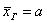 ), и поэтому дисперсию нужно обязательно поправить: ), и поэтому дисперсию нужно обязательно поправить:
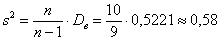 – несмещённая оценка неизвестной генеральной дисперсии – несмещённая оценка неизвестной генеральной дисперсии 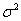 . И нас будет интересовать несмещённая оценка генерального стандартного отклонения . И нас будет интересовать несмещённая оценка генерального стандартного отклонения 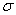 : :
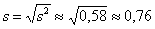 – исправленное среднее квадратическое отклонение. – исправленное среднее квадратическое отклонение.
Теперь построим доверительный интервал для оценки истинного (генерального) значения 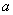 величины величины 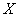 . .
Если генеральное стандартное отклонение 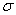 не известно не известно
, то этот интервал строится по похожей формуле:
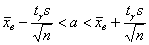 , с той поправкой, что коэффициент доверия , с той поправкой, что коэффициент доверия 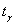 рассчитывается с помощью распределения Стьюдента. рассчитывается с помощью распределения Стьюдента.
Вычислим точность оценки:
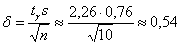
Таким образом, искомый доверительный интервал:
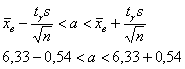
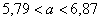 – данный интервал с вероятностью – данный интервал с вероятностью 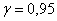 накрывает истинное значение накрывает истинное значение 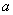 измеряемой величины измеряемой величины 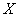 . .
Ответ: 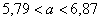
Пример 3
По 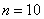 равноточным измерениям найдено исправленное среднее квадратическое отклонение равноточным измерениям найдено исправленное среднее квадратическое отклонение 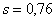 . Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения . Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения 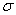 (генерального стандартного отклонения) с надёжностью (генерального стандартного отклонения) с надёжностью 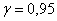 . .
Решение: Доверительный интервал для оценки неизвестной дисперсии 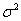 нормально распределённой генеральной совокупности определяется следующим образом: нормально распределённой генеральной совокупности определяется следующим образом:
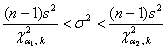 , где , где 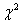 – распределение «хи-квадрат», а – распределение «хи-квадрат», а 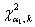 , , 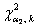 – его критические значения, вычисленные для – его критические значения, вычисленные для 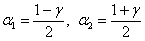 , , 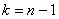
Данный интервал с вероятностью 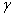 (надёжностью) накрывает истинное значение (надёжностью) накрывает истинное значение 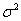 . И если из всех частей неравенства извлечь корни, то получим соответствующий интервал для оценки генерального стандартного отклонения: . И если из всех частей неравенства извлечь корни, то получим соответствующий интервал для оценки генерального стандартного отклонения:
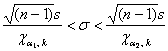
Значения 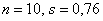 известны, и вычислим: известны, и вычислим:
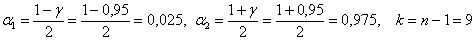
и теперь, по таблице критических значений распределения 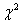 находим: находим:
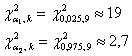
Получены различные значения, и наш доверительный интервал будет асимметричным (ввиду асимметрии распределения «хи-квадрат»):
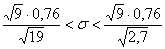 – не забываем извлечь корни из знаменателей! – не забываем извлечь корни из знаменателей!
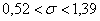 – таким образом, с вероятностью – таким образом, с вероятностью 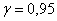 можно утверждать, что данный интервал накроет генеральное стандартное отклонение можно утверждать, что данный интервал накроет генеральное стандартное отклонение 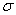 . .
Ответ: 1) 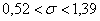 , 2) , 2) 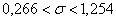 . .
Пример 4
В результате обработки экспериментальных данных объёма 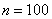 мы получили следующие выборочные характеристики: мы получили следующие выборочные характеристики: 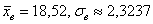 . .
В предположении о нормальном распределении генеральной совокупности, с надёжностью 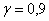 определить доверительные интервалы: определить доверительные интервалы:
1) для оценки неизвестной генеральной средней 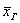 ; ;
2) для оценки генерального среднего квадратического отклонения 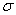 двумя способами – с помощью распределения хи-квадрат: двумя способами – с помощью распределения хи-квадрат: 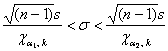 и приближённо, по формуле и приближённо, по формуле 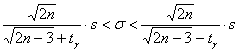 , где , где 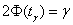 . .
И заметьте, что здесь «плакал» лёгкий способ построения интервала 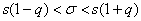 , так как в стандартной таблице отсутствуют значения для , так как в стандартной таблице отсутствуют значения для 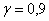 . .
Решение: вычислим исправленное среднеквадратическое отклонение:
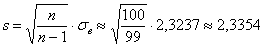
1) Определим доверительный интервал 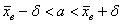 , где , где 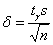 . .
Для уровня доверительной вероятности 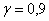 и объёма выборки и объёма выборки 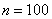 по соответствующей таблице найдём по соответствующей таблице найдём 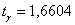 . .
Вычислим точность оценки:
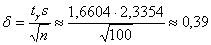
Таким образом:
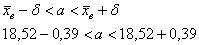
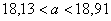 – с вероятностью – с вероятностью 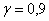 данный интервал накроет генеральное среднее значение данный интервал накроет генеральное среднее значение 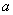 . .
2) Найдём доверительный интервал для генерального стандартного отклонения 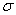 . .
а) С помощью распределения 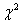 : :
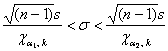
Вычислим 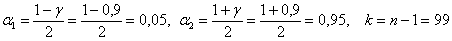 и с помощью соответствующей функции Экселя найдём: и с помощью соответствующей функции Экселя найдём:
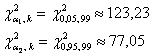
Таким образом:
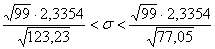
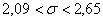 – искомый интервал, накрывающий генеральное значение – искомый интервал, накрывающий генеральное значение 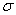 с вероятностью с вероятностью 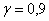 . .
б) Дадим интервальную оценку приближенно, с помощью формулы:
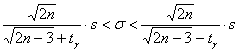
Коэффициент доверия найдём из соотношения 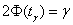 . В данном случае: . В данном случае:
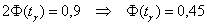 , и с помощью таблицы , выясняем, что , и с помощью таблицы , выясняем, что 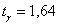 . .
Таким образом:
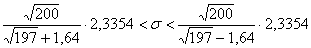
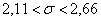 – искомый интервал. – искомый интервал.
Ответ:
1) 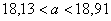 , ,
2) 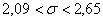 с помощью распределения с помощью распределения 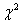 и и 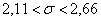 приближённо. приближённо.
Задание на дом.
По результатам выборочного исследования 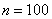 объектов найдена выборочная средняя объектов найдена выборочная средняя 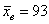 . .
1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения менее чем на 3, если известно, что генеральная совокупность распределения нормально с дисперсией 400?
2) Определить доверительный интервал, который с надежностью 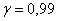 накроет истинное значение генеральной средней. накроет истинное значение генеральной средней. |
|
|
 Скачать 78.16 Kb.
Скачать 78.16 Kb.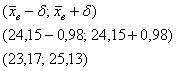

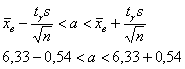
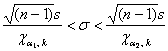
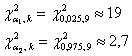
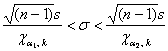 и приближённо, по формуле
и приближённо, по формуле 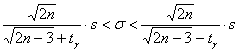 , где
, где