теория вероятности. 1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы

• Название: 1. Опыт с равновероятностными исходами. Вероятность и частота. Некоторые комбинаторные формулы
• Дата: 23.04.2022
• Размер: 1.11 Mb.
• Имя файла: теория вероятности.doc
• Тип: Документы; #492247
• страница: 2 из 5

а) для всех i;
б) .

То есть случайная величина ξ имеет дискретное распределение, если она принимает не более чем счетное число значений.

Виды дискр.распр-ний: вырожденное распр., распр. Бернулли, биноминальное распр., геометрическое распр., распр. Пуассона, гипергеометрическое распр. и др.
Вырожденное распределение.
Говорят, что случайная величина ξ имеет вырожденное распределение с параметром а, если ξ принимает единственное значение а с вероятностью 1, то естьР(ξ=а)=1. Таблица распределения ξ имеет вид

ξ	а
Р	1

Испытания Бернулли

Одинаковые, независ.между собой испытания, в каждом из к-рых рассматривается некотор.соб.А, наступающее с некотор.положит.вер-тью Р=Р(А)0, нзв испытаниями Бернулли. Само соб.А нзв успехом, а Ā – неудачей. р – вер-ть успеха; q – вер-ть неуспеха. q=1-р.
Распределение Бернулли.
Говорят, что случайная величина ξ имеет распределение Бернулли с параметром р, если ξ принимает значения 1 и 0 с вероятностями р и 1-р, соответственно. Случайная величина ξ с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха р (0 успехов или 1 успех). Таблица распределения ξ имеет вид

ξ	0	1
Р	1-р	р

Биноминальное распределение

Говорят, что случайная величина ξ имеет биномиальное распределение с параметрами n и p, где 0p1, если ξ принимает значения 0, 1,…, n с вероятностями . Случайная величина ξ с таким распределением имеет смысл числа успехов в nиспытаниях схемы Бернулли с вероятностью успеха p.
Таблица распределения ξ имеет вид



ξ – может быть представл в виде суммы независ-ых событий ξ_k.

ξ_k = 0 – неуспех

ξ_k =1 – успех

ξ= ξ₁+ ξ₂+…+ ξ_k

M[ξ_k]=P

D[ξ_k]=M[ξ_k ²]-[M[ξ_k]²]=p-p²=pq

=> M[ξ]=np

D[ξ]=npq
Распределение Пуассона

Говорят, что случайная величина ξ имеет распределение Пуассона с параметром , где >0, если ξ принимает значения 0, 1, 2… с вероятностями
Таблица распределения ξ имеет вид



Ф-ция распределения:

где а – мат.ожидание









Замечание: распр Пуассона явл предельным, к кот-му → биноминальное распр при n→∞ и a=np=const.
Теорема Пуассона.

n – большое число испытаний

p – достаточно малая вер-ть

np – число успехов – значительно



a=np – среднее число успехов

Док-во:



р=a/n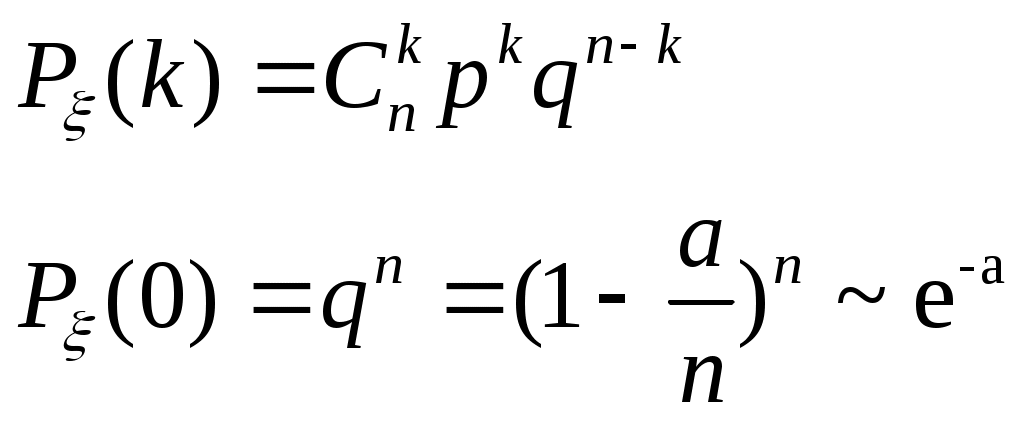













Теорема: Пусть число исп-ий n →∞, а P→0, так что среднее число успехов np=a>0, тогда для любого k≥0 вер-ть получить k успехов в n исп-ях схемы Бернулли с вер-тью P по формуле:



n∞, P0, np=const>0, то




12. Основные непрерывные распределения. Равномерное распределение. Экспоненциальное распределение. Нормальное распределение. Логарифмически нормальное распределение.

Основные непрерывные распределения

Случайная величина ξ имеет абсолютно непрерывное распределение, если существует неотрицательная функция f_ξ(x) такая, что для любого xR функция распределения F_ξ(x) представима в виде



При этом функция f_ξ(x) называется плотностью распределения случайной величины ξ.

Виды непрерывных распред.: равномерное, нормальное (гауссовское), показательное (экспоненциальное), логарифмически нормальное.
Равномерное распр.

С 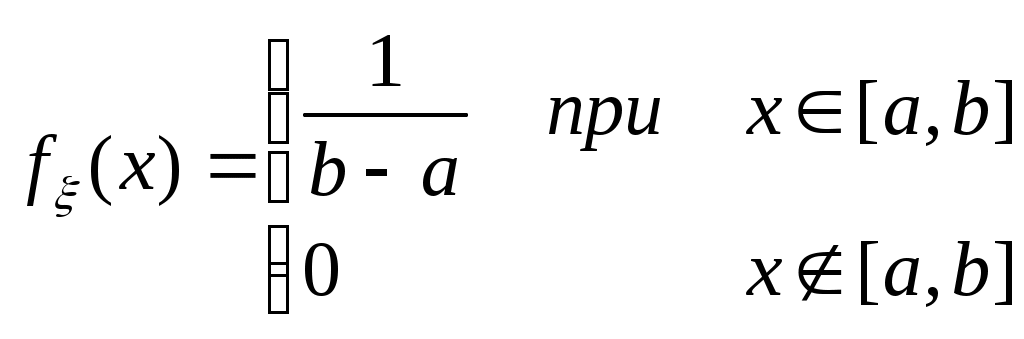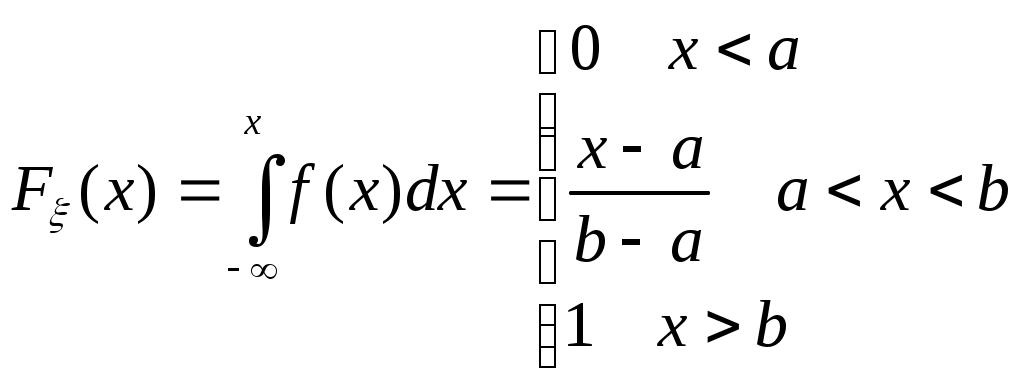л вел-на ξ имеет равномер распред на отрезке [a;b] с несчет мн-вом возм значений, если плотность распр ξ постоянна на отрезке [a;b] и = 0 вне его.












Равномер распр явл непрерывным аналогом дискр распр-я вер-ей для опытов с равновероятностными исходами.
Экспоненциальное распределение.

С 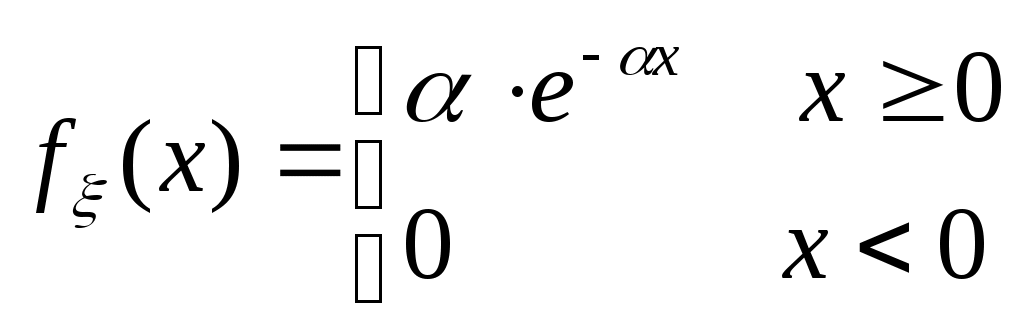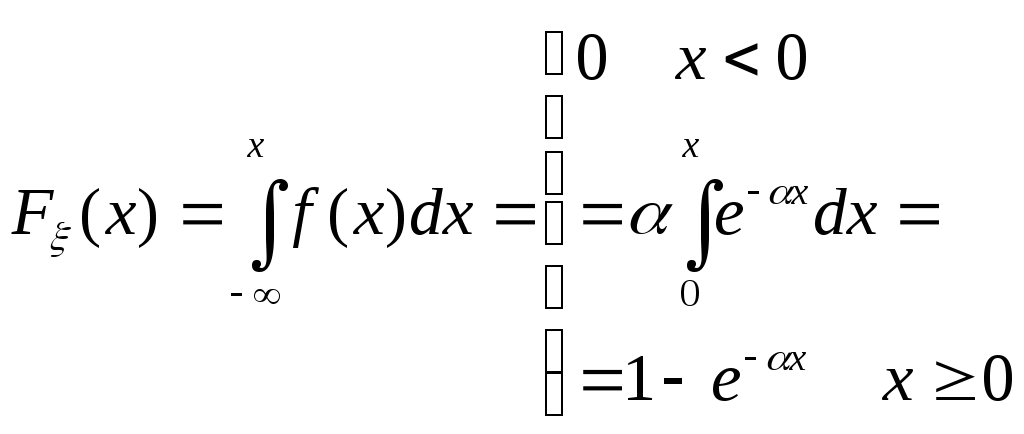луч вел-на ξ имеет экспоненц-ое (показательное) распр с параметром α>0, если имеет место след посл-ть распределения:












Нормальное распределение.

Опред: Случ вел-на ξ имеет нормальное (Гауссовское) распр-е с параметрами a и σ (σ >0), если имеет место след плотность распр-ия:























Свойства:

1. F_a,σ ²(x)=F_0,1((x-a)/σ)

xR

2. ξ (x₁, x₂)

P(x₁≤ξ≤ x₂)=Ф((x₂-a)/σ) – Ф((x₁-a)/σ)

3. Ф-ция распр сл вел-ны ξ, распред-ой по норм закону, выражается через ф-цию Лапласа по формуле:

F_ξ(x)=½+Ф((x-a)/σ)
Логарифмически нормальное распределение.

Опред: Лог-ски норм распр-ем наз-ся распр-ие вер-ти неотриц случайной вел-ны ξ, логарифм кот-ой распределен по норм-му закону с параметрами a и σ, σ>0.

a=M[ln ξ]

σ²=D[ln ξ]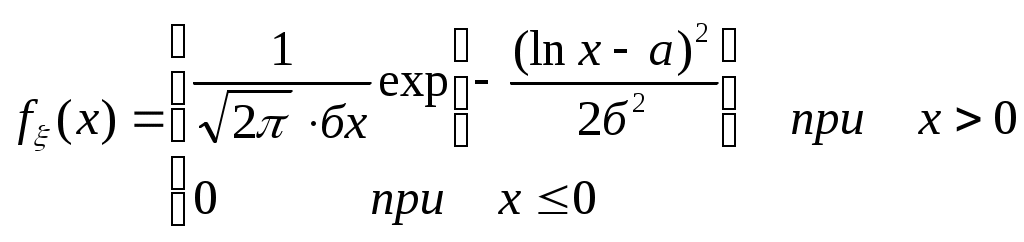










Числовые характеристики: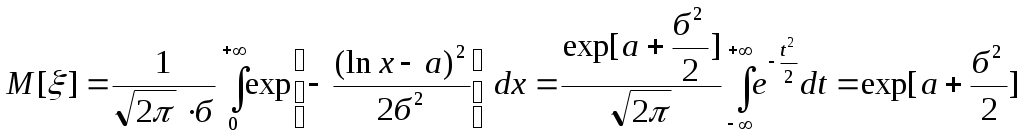




13. Закон больших чисел. Неравенство Чебышёва. Правило 3σ. Теорема Чебышёва. Теорема Бернулли. Центральная предельная теорема. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.

Закон больших чисел

Свойства статистической устойчивости средних заключается в том, что индивидуальные особенности, присущие каждому конкретному случайному явлению, почти не сказываются на усредненном результате таких явлений.

Закон больших чисел – это несколько теорем, определяющих общие условия, при которых среднее значение случайных величин стремится к некоторой const при проведении большого числа опытов (теоремы Чебышева и Бернулли).



Если существует последовательность

таких, что для любых ε>0, выполняется условие:

(*)

Последовательность подчиняется закону больших чисел с заданными функциями :



Если в выражении (*) , то говорят, что случайная величина сходится по вероятности к а.

В данных терминах означает, что вел-на η_n-a_n сходится по вероятности к нулю.
Неравенство Чебышева

Для любой случайной величины ξ(кси), имеющей M[ξ] и D[ξ] при каждом ε>0 имеет место неравенство(неравенство Чебышева):
Док-во:

ξη, M[ξ]M[η]

Рассмотр. некотор.сл.вел-ну η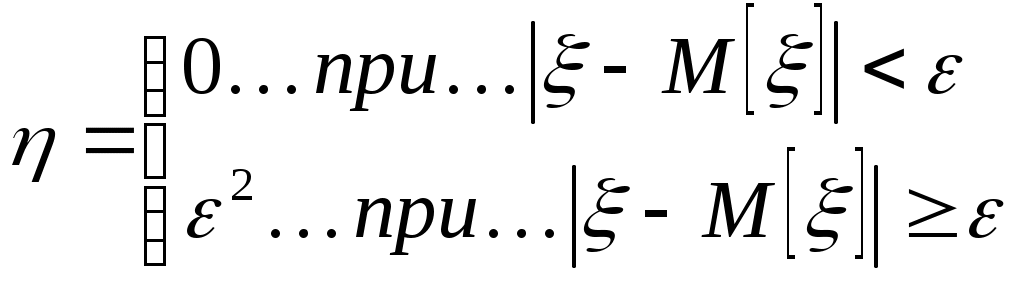







Пример: пусть ε=3σ

Случайная величина окажется за пределами 3σ:



Верно для любого распределения. Это – верхняя граница распределения вер-ти.

Противоположное событие – в пределах 3σ:


Правило 3σ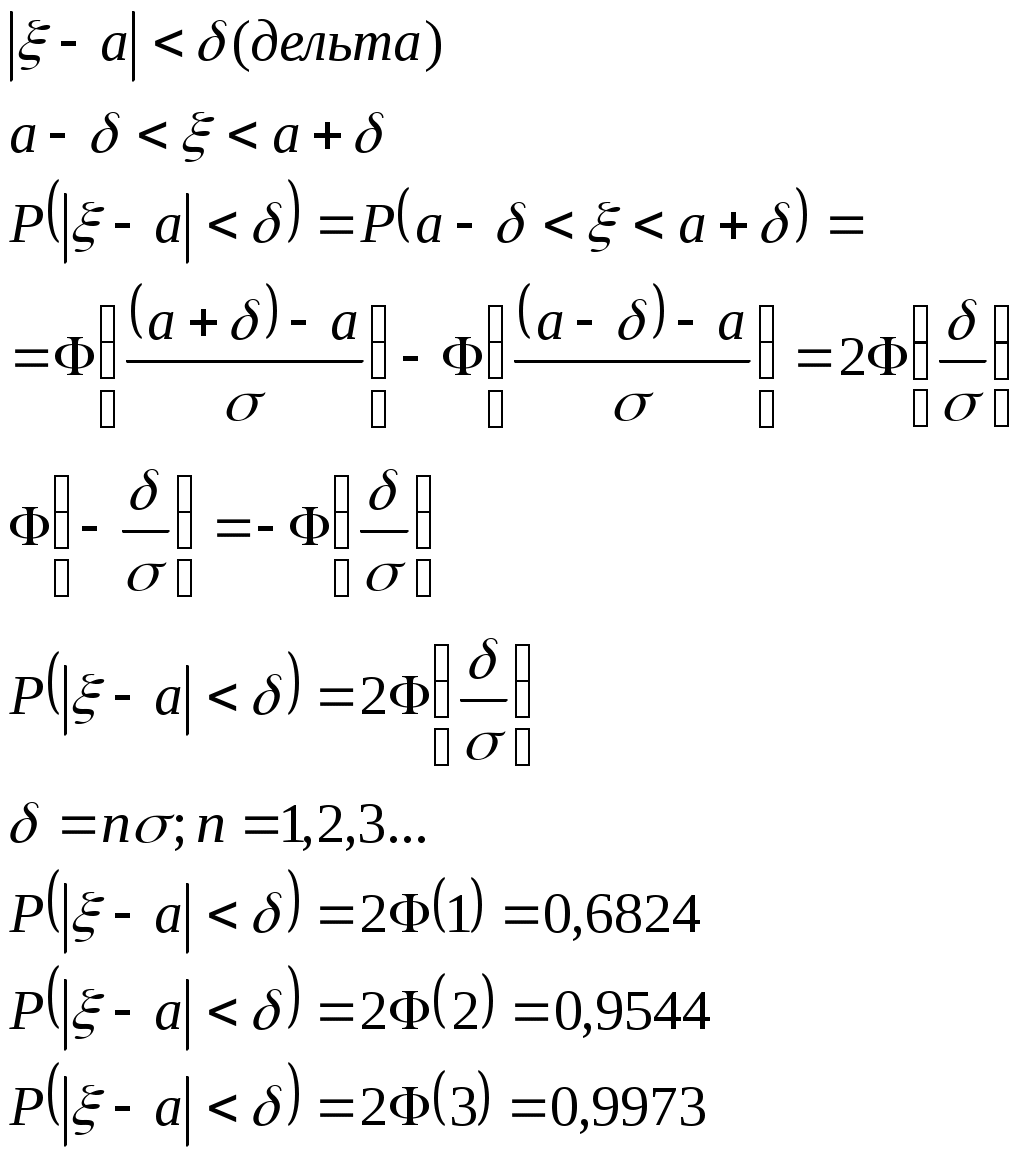



99,73%

0,27% - неудача (практически невозможное событие)

Правило 3σ:

Если случайная величина имеет нормальное распределение, то отклонение этой величины от мат ожидания по абсолютной величине не превосходит утроенного среднеквадратического отклонения.
Теорема Чебышева

Если 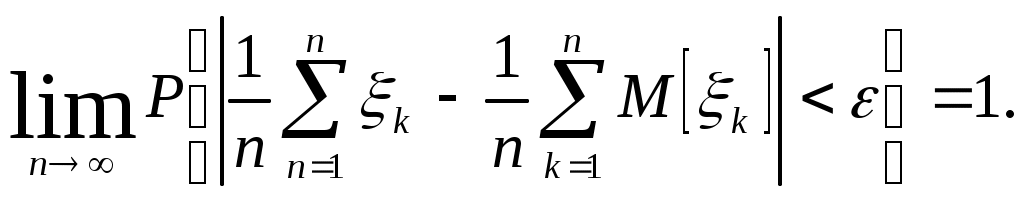последовательность попарнонезависмых случайных величин, имеющих конечное мат ожидание и дисперсия, ограниченная одной и той же постоянной то при любом ε>0, предел вероятности события стремится к 1 при n→∞:


Док-во: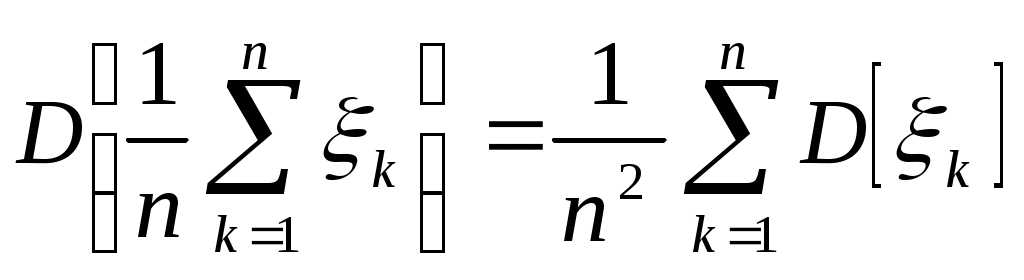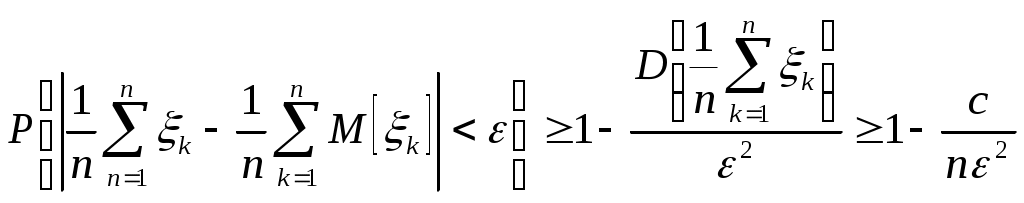









следовательно, при n→∞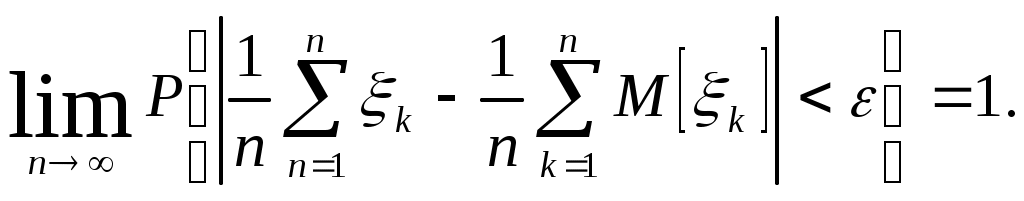


Теорема Бернулли

Пусть m – число наступлений события А в n независимых испытаний и Р – вероятность наступления события А в каждом из испытаний при любом ε>0.



С ростом числа испытаний относительная частота успехов (m/n) будет приближаться к единичной вероятности.

Вводим случайную величину 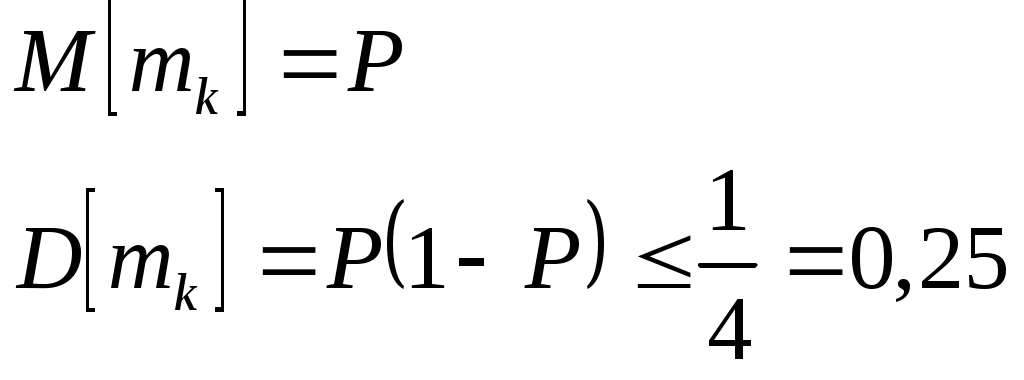- число наступлений события А в k-ом испытании.




Центральная предельная теорема

Если 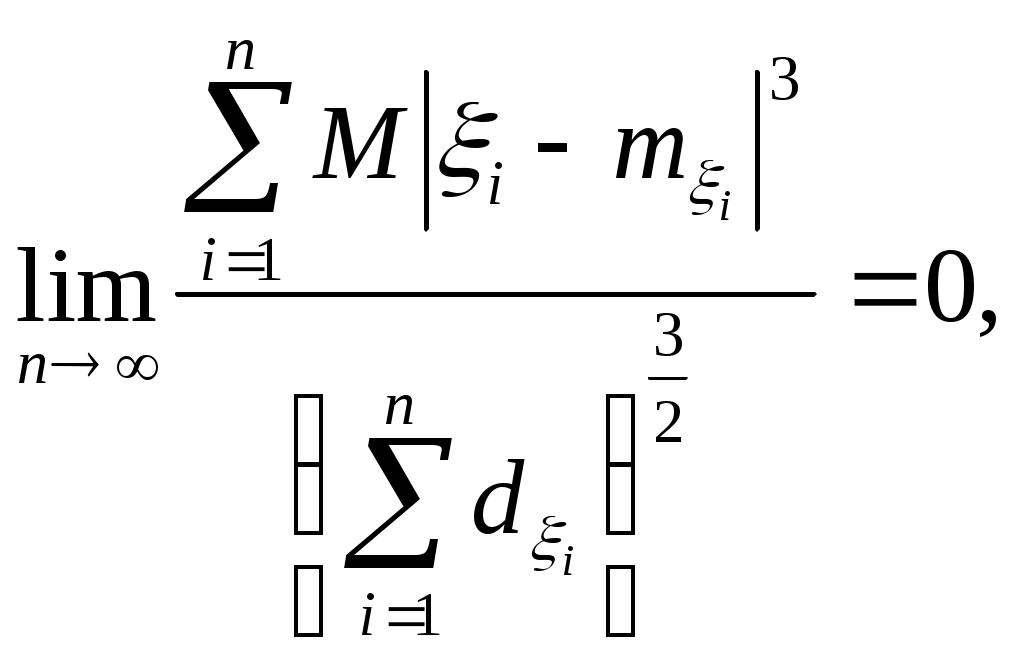независимые случайные величины, имеющие и третий центральный абсолютный момент: и если выполняется условие Ляпунова:

то при неограниченном возрастании n (n→∞) закон распределения суммы случайных величин 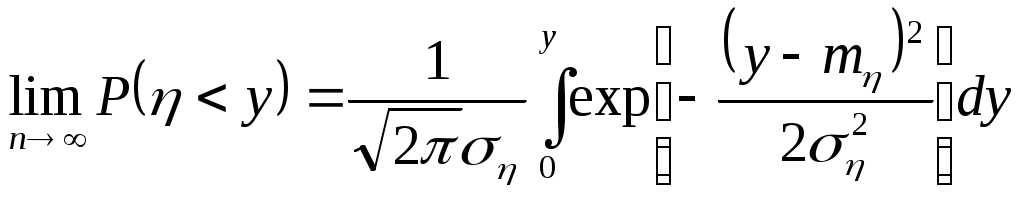неограниченно приближается к нормальному закону с параметрами:





Пусть 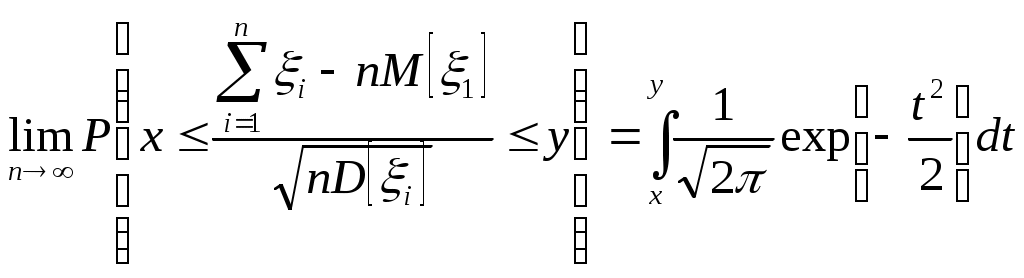независимые случайные величины с конечной ненулевой дисперсией, тогда для любых вещественных чисел х и у, х<у, n→∞ имеет место следующий вид сходимости:


Локальная предельная теорема Муавра-Лапласа

Если вероятность наступления некоторого события в n независимых испытаниях постоянна и равна Р (0<Р<1), то вероятность 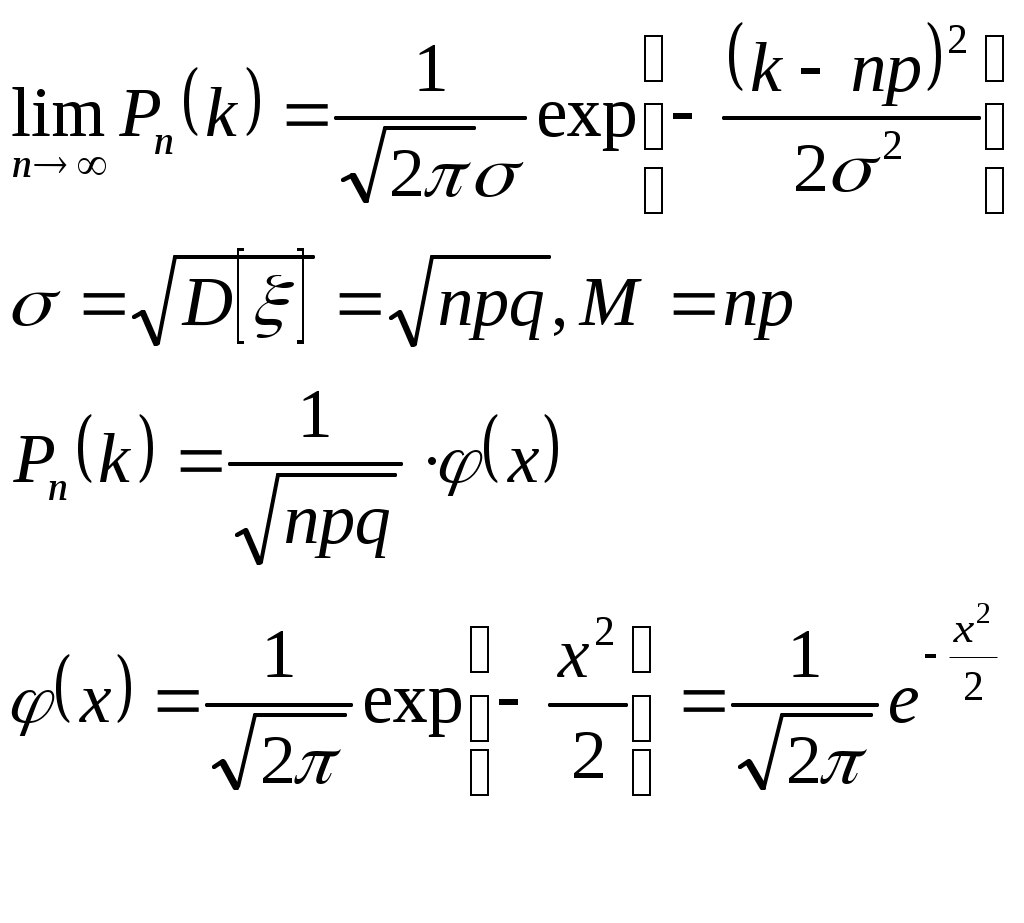того, что в этих испытаниях событие А наступит ровно k раз при n→∞ удовлетворяет соотношению:

для х>0

φ(-х)=φ(х)
Интегральная теорема Муавра-Лапласа

Если k – число наступления события в n независимых испытаниях, в каждом из которых вероятность этого события = Р, то равномерно относительно а и b, связанных так: – ∞ ≤ а ≤ b ≤ + ∞, имеет место соотношение при n→∞:



Функция Лапласа: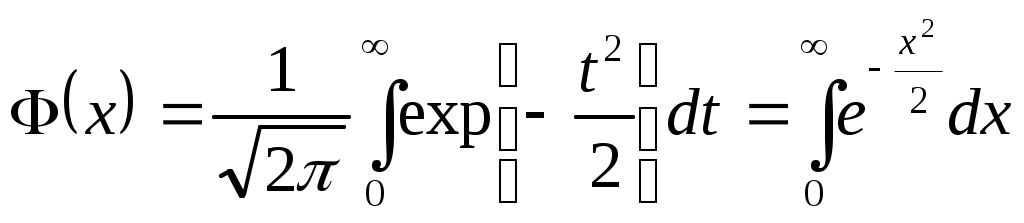



Ф( – х)= – Ф(х)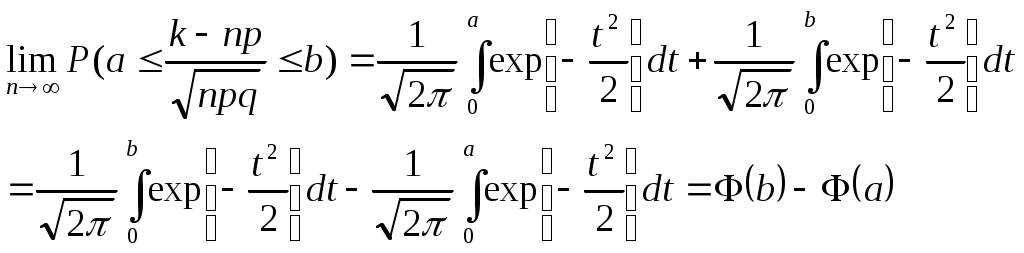



при n→∞.

Если n конечно


14. (1.)Векторные случайные величины. (2.)Свойства двумерной случайной величины. (3.)Двумерная дискретная случайная величина, её геометрическая интерпретация. (4.)Функция распределения и её свойства. (5.)Матрица распределения. (6.)Двумерная непрерывная случайная величина, её геометрическая интерпретация. (7.)Плотность распределения двумерной случайной величины и её свойства. (8.)Понятие независимости для двумерных случайных величин. (9.)Критерии независимости.

(1.) Кроме одномерных, случайных величин можно рассматривать многомерные, случайные векторы, координаты которых являются одномерными, случайными величинами. Пример:

1) Успеваемость ученика

2)Погода в данное время в данном месте.

Случайная векторная величина принимает каждый раз значения, зависящие от элементарного события. Таким образом, многомерная, случайная величина есть вектор-функция, заданная на пространстве элементарных событий, и каждое ее возможное значение есть вектор.

Будем обозначать через (X, Y) двумерную сл.вел-ну. Каждую из вел-н Х и Y нзв составляющей (компонентой); обе вел-ны Х и Y, рассматриваемые одновременно, образуют систему двух сл.вел-н. Аналогично n-мерную вел-ну можно рассматривать как систему n сл.вел-н. Например, трехмерная вел-на (X, Y, Z) определяет систему трех сл.вел-н X, Y и Z. Целесообразно различать дискретные (составляющие этих вел-н дискретны) и непрерывные (составляющие этих вел-н непрерывны) многомерные сл.вел-ны.

В теоретеко-множественной трактовке любая случайная величина X_i(i=1,2,…n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω (ωΩ).

Поэтому и многомерная случайная величина есть функция элементарных событий ω, т.е. каждому элементарному событию ставится в соответствие несколько действительных чисел х₁,х₂,…x_n , которые приняли случайные величины Х₁,Х₂, …Х_n в результате испытания. В этом случае вектор х=(х₁,х₂,…х_n) называется реализацией случайного вектора Х= (Х₁,Х₂, …Х_n).

На вероятностном пространстве {Ω,F,P} определены n-мерные сл.вел-ны ξ₁=f₁(), ξ₂=f₂(), …, ξ_n=f_n() (f_i() измеримы). Вектор (ξ₁, ξ₂,…, ξ_n) нзв случ.вектором или n-мерной сл.вел-ной. Обозначим мн-во элемент.событий  {ξ₁1, ξ₂2, …, ξ_nn}, для к-рых одноврем.выполняется неравенство f₁()1, f₂()2, …, f_n()n, при этом {ξ₁1, ξ₂2, …, ξ_nn}F. Тогда при любом наборе х₁, х₂,…,x_n выполняется равенство F(х₁, х₂,…,x_n)=P{ξ₁1, ξ₂2,…, ξ_nn}. Эта ф-ция n-аргументов нзв n-мерной ф-цией распределения сл.вектора (ξ₁, ξ₂,…, ξ_n).

Многомерная случайная величина полностью определяется ее функцией распределения вероятностей, удовл. след.условиям:

1. 0 F(х₁, х₂,…,x_n)1

2. F(х₁, х₂,…,x_n) не убывает по каждому аргументу

3.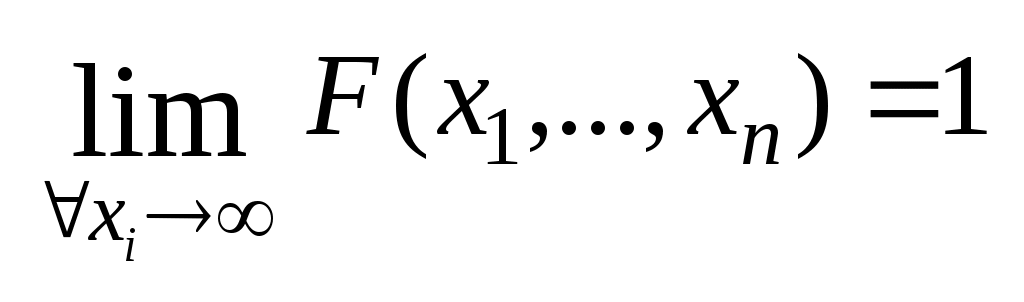

4. 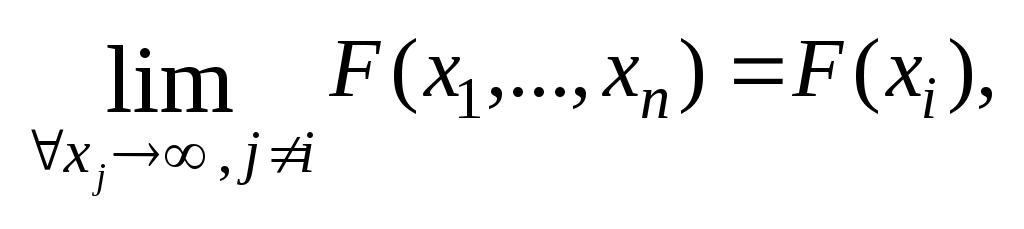где F(x_i) – ф-ция распред.одномерной сл.вел-ны ξ_i.

(2.) Двумерная сл.вел-на (ξ, ) – это совокупность 2-х одномерных сл.вел-н, к-рые принимают значения в рез-те проведения одного и того же опыта. Двумерные сл.вел-ны характеризуются мн-вами значений Ω_ξ и Ω_ своих компонент и совместными (двумерными) законами распределения. В зав-ти от типа компонент ξ и , различают дискретные, непрерывные и смешанные сл.вел-ны.

(3.) Двумерная случайная величина называется дискретной, если составляющие ее случайные величины являются дискретными. Двумерную сл.вел-ну (ξ, η) геометрически можно изобразить либо как случайную точку М(ξ, ) на плоскости (т.е. как точку со случ.координатами), либо как случ.вектор ОМ.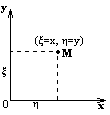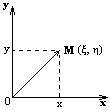




(4.) Ф-цией распред. F_ξη(x, y) двумерной сл.вел-ны (ξ, η) нзв вер-ть совместного выполнения события (ξξη(x, y)=Р(ξ
Г еометрически это можно истолковать так: F_ξη(x, y) есть вер-ть того, что случ.точка (ξ, η) попадет в бесконечный квадрант с вершиной (х, у), расположенные левее и ниже этой вершины.
Св-ва ф-ции распределения двумерной сл.вел-ны:

1. 0 F_ξη(x, y)1 Вытекает из опред-я ф-ции рапред.как вер-ти: вер-ть – всегда неотриц.число, не превышающее 1.

2. F_ξη(x, +∞)= F_ξ(x), т.к. F_ξη(x, +∞)=Р(ξξ(x)

F_ξη(+∞, y)= F_η(y) аналогично

3. F_ξη(x, -∞)= F_ξη(-∞, у)= F_ξη(-∞, -∞)=0. Вытекает из невозможности событий.

F_ξη(+∞, +∞)=1. Вытекает из достоверности событий.

4. F_ξη(x, y) есть монотонно неубывающая ф-ция по каждому аргументу.

Д-во: Событие, состоящее в том, что составляющая ξ примет значение, меньшее х₂, и при этом составляющая η1, и при этом η1, η<у); 2) ξ примет значение, удовлетворяющее нер-ву х₁ξ<х₂, и при этом η1ξ<х₂, η2, η<у)= Р(ξ1, η<у)+ Р(х₁ξ<х₂, η2, η<у) – Р(ξ1, η<у) = Р(х₁ξ<х₂, ηξη(x₂, y) - F_ξη(x₁, y)= Р(х₁ξ<х₂, ηξη(x₂, y) - F_ξη(x₁, y)0, или F_ξη(x₂, y)F_ξη(x₁, y) ч.т.д. Аналогично доказывается, что F_ξη(x, y) неубывающая по аргументу у.

5 . Если двумерн.ф-ция распред. F_ξη(x, y) непрерывна по х и по у, то вер-ть попадания случ.вел-ны (ξ, η) в прямоугольную область D={х₁  x  х₂, y₁  y y₂} равна Р(х₁ξх₂, у₁ η у₂) = F(x₁, y₁)+F(x₂, y₂) – F(x₁, y₂) – F(x₂, y₁).
(5.) Законом распред.дискретной двумерной сл.вел-ны нзв перечень возможных значений этой вел-ны, т.е пар чисел (x_i, y_j) и их вероятностей р(x_i, y_j) (i=1, 2,…,n; j=1, 2,…, m). Обычно закон распределения задают в виде матрицы. Матрица распред.предст.соб.таблицу, к-рая содержит значения {x₁, x₂,…, x_n}, {y₁, y₂,…, y_n} и вероятности возможных пар значений P_ij=P(ξ=x_i; η=y_j) (i=1, 2,…,n; j=1, 2,…, m).

	y1	y2	…	ym
x1	P11	P12	…	P1m
x2	P21	P22	…	P2m
…	…	…	…	…
xn	Pn1	Pn2	…	Pnm

Св-ва:

1)

2) ,

3) ,

(6.) Двумер.сл.вел-на (ξ, η) является непрерывной, если ее ф-ция распред.предст.соб. непрерывную дифференцированную ф-цию по каждому из аргументов и существует 2-ая смешанная производная. Пространством ее элементарных событий является плоскость, либо область плоскости, либо область конечной ненулевой плоскости.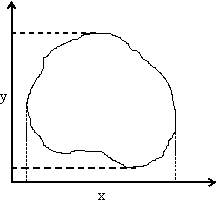



(7.) Двумерной плотностью ф-ции распред. f_ξη(x, y) случ.вел-ны (ξ, η) нзв предел отношения вер-ти попадания случ.точки в элементарный участок плотности, примыкающий к точке (х, у), к площади этого участка, когда его размер стремится к 0.

Т.о. плотностью совместного распределения вер-тей двумерной непрерывной сл.вел-ны нзв вторую смешанную частную производную от ф-ции распред. Геометрически эту ф-цию можно истолковать как поверхность, к-рую нзв поверхностью распределения.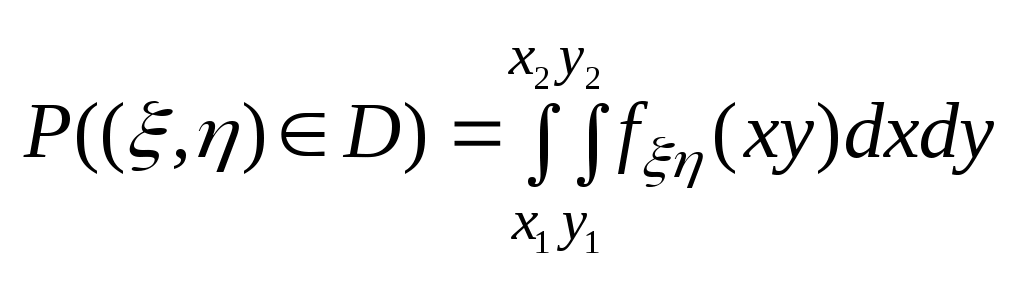

D={х₁ ξ х₂, у₁ η у₂}
Свойства двумерной плотности распределения:

1)

2) Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен 1.



3)

4)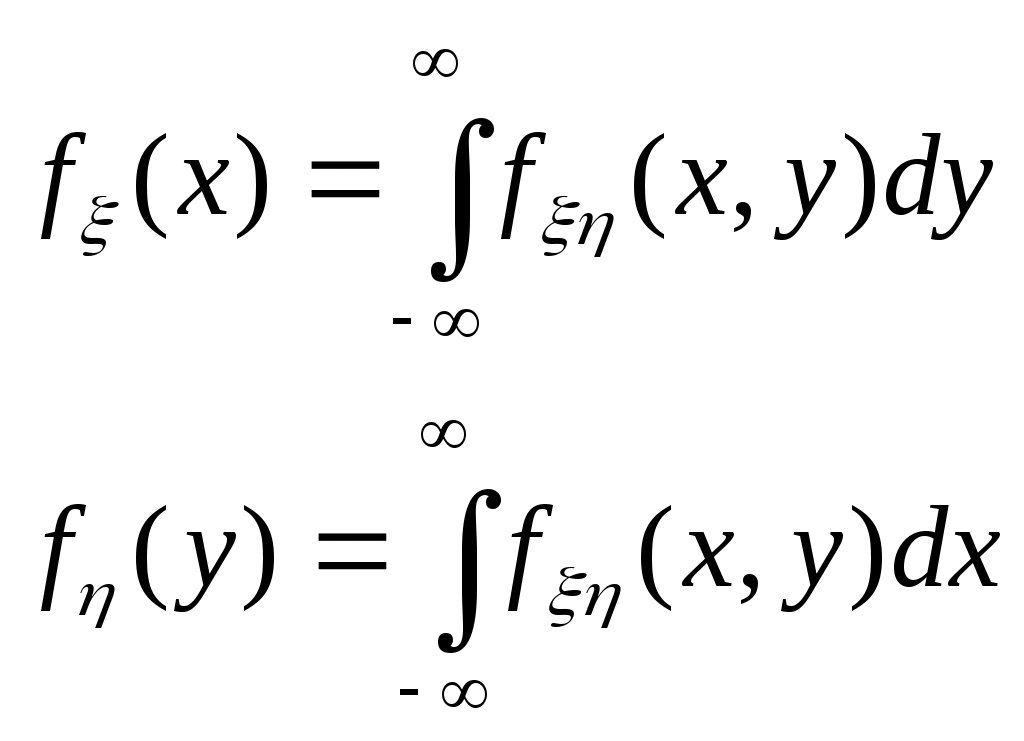

(8.) Величина ξ независима от величины η ,если её закон распределения не зависит от того, какое значение принимает величина η.