Лекция. Повторные независимые испытания лекция. Повторные независимые испытания
 Скачать 252 Kb. Скачать 252 Kb.
|
|
Повторные независимые испытания На практике приходится сталкиваться с такими задачами, которые можно представить в виде многократно повторяющихся испытаний, в результате каждого из которых может появиться или не появиться событие . При этом интерес представляет исход не каждого "отдельного испытания, а общее количество появлений события в результате определенного количества испытаний. В подобных задачах нужно уметь определять вероятность любого числа появлений события в результате испытаний. Рассмотрим случай, когда испытания являются независимыми и вероятность появления события в каждом испытании постоянна. Такие испытания называются повторными независимыми. Примером независимых испытаний может служить проверка на годность изделий, взятых по одному из ряда партий. Если в этих партиях процент брака одинаков, то вероятность того, что отобранное изделие будет бракованным, в каждом случае является постоянным числом. Формула Бернулли Воспользуемся понятием сложного события, под которым подразумевается совмещение нескольких элементарных событий, состоящих в появлении или непоявлении события в –м испытании. Пусть проводится независимых испытаний, в каждом из которых событие может либо появиться с вероятностью , либо не появиться с вероятностью . Рассмотрим событие , состоящее в том, что событие в этих испытаниях наступит ровно раз и, следовательно, не наступит ровно раз. Обозначим Событие может появиться раз в разных последовательностях или комбинациях, чередуясь с противоположным событием . Число возможных комбинаций такого рода равно числу сочетаний из элементов по , т. е. . Следовательно, событие можно представить в виде суммы сложных несовместных между собой событий, причем число слагаемых равно : где в каждое произведение событие входит раз, а — раз. Вероятность каждого сложного события, входящего в формулу (3.1), по теореме умножения вероятностей для независимых событий равна . Так как общее количество таких событий равно , то, используя теорему сложения вероятностей для несовместных событий, получаем вероятность события (обозначим ее )
Формулу (3.2) называют формулой Бернулли, а повторяющиеся испытания, удовлетворяющие условию независимости и постоянства вероятностей появления в каждом из них события , называют испытаниями Бернулли, или схемой Бернулли. Пример 1. Вероятность выхода за границы поля допуска при обработке деталей на токарном станке равна 0,07. Определить вероятность того, что из пяти наудачу отобранных в течение смены деталей у одной размеры диаметра не соответствуют заданному допуску. Решение. Условие задачи удовлетворяет требования схемы Бернулли. Поэтому, полагая Пример 2. Наблюдениями установлено, что в некоторой местности в сентябре бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми? Решение. Наивероятнейшее число появлений события Наивероятнейшим числом появления события в независимых испытаниях называется такое число , для которого вероятность, соответствующая этому числу, превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных чисел появления события . Для определения наивероятнейшего числа не обязательно вычислять вероятности возможных чисел появлений события, достаточно знать число испытаний и вероятность появления события в отдельном испытании. Обозначим вероятность, соответствующую наивероятнейшему числу . Используя формулу (3.2), записываем
Согласно определению наивероятнейшего числа, вероятности наступления события соответственно и раз должны, по крайней мере, не превышать вероятность , т. е. Подставляя в неравенства значение и выражения вероятностей и , получаем 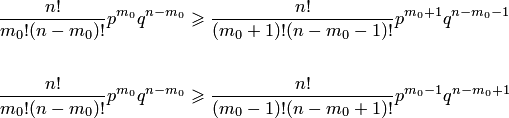 Решая эти неравенства относительно , получаем Объединяя последние неравенства, получаем двойное неравенство, которое используют для определения наивероятнейшего числа:
Так как длина интервала, определяемого неравенством (3.4), равна единице, т. е. и событие может произойти в испытаниях только целое число раз, то следует иметь в виду, что: 1) если — целое число, то существуют два значения наивероятнейшего числа, а именно: и 2) если — дробное число, то существует одно наивероятнейшее число, а именно: единственное целое, заключенное между дробными числами, полученными из неравенства (3.4); 3) если — целое число, то существует одно наивероятнейшее число, а именно: . При больших значениях пользоваться формулой (3.3) для расчета вероятности, соответствующей наивероятнейшему числу, неудобно. Если в равенство (3.3) подставить формулу Стирлинга
Пример 2. Известно, что часть продукции, поставляемой заводом на торговую базу, не удовлетворяет всем требованиям стандарта. На базу была завезена партия изделий в количестве 250 шт. Найти наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, и вычислить вероятность того, что в этой партии окажется наивероятнейшее число изделий. Решение. По условию откуда Локальная теорема Лапласа Пользоваться формулой Бернулли при больших значениях очень трудно. Например, если Естественно, возникает вопрос: нельзя ли вычислить интересующую вероятность, не используя формулу Бернулли? Оказывается, можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления событий ровно раз в испытаниях, если число испытаний достаточно велико. Теорема 3.1. Если вероятность появления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в испытаниях ровно раз, приближенно равна (тем точнее, чем больше ) значению функции Существуют таблицы, которые содержат значения функции Итак, приближенно вероятность того, что событие появится в испытаниях ровно раз, Пример 3. Найти вероятность того, что событие наступит ровно 80 раз в 400 испытаниях, если вероятность появления события в каждом испытании равна 0,2. Решение. По условию Вычислим определяемое данными задачи значение : По таблице прил, 1 находим Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены): Интегральная теорема Лапласа Предположим, что проводится независимых испытаний, в каждом из которых вероятность появления события постоянна и равна . Необходимо вычислить вероятность того, что событие появится в испытаниях не менее и не более раз (для краткости будем говорить "от до раз"). Это можно сделать с помощью интегральной теоремы Лапласа. Теорема 3.2. Если вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, то приближенно вероятность того, что событие появится в испытаниях от до раз, 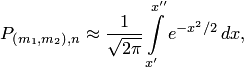 где где При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл 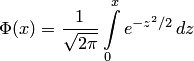 приведена в прил. 2, где даны значения функции для положительных значений , для используют ту же таблицу (функция нечетна, т. е. приведена в прил. 2, где даны значения функции для положительных значений , для используют ту же таблицу (функция нечетна, т. е. Итак, приближенно вероятность того, что событие появится в независимых испытаниях от до раз, Пример 4. Вероятность того, что деталь изготовлена с нарушениями стандартов, . Найти вероятность того, что среди 400 случайно отобранных деталей нестандартных окажется от 70 до 100 деталей. Решение. По условию Вычислим пределы интегрирования: нижний верхний Таким образом По таблице прил. 2 находим Искомая вероятность Применение интегральной теоремы Лапласа Если число (число появлений события при независимых испытаниях) будет изменяться от до , то дробь
Поставим задачу найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства
Пример 5. Вероятность того, что деталь нестандартна, . Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности по абсолютной величине не более чем на 0,03. Решение. По условию По таблице прил. 2 находим Формула Пуассона для маловероятных событий Если вероятность наступления события в отдельном испытании близка к нулю, то даже при большом числе испытаний , но при небольшом значении произведения получаемые по формуле Лапласа значения вероятностей оказываются недостаточно точными и возникает потребность в другой приближенной формуле. Теорема 3.3. Если вероятность наступления события в каждом испытании постоянна, но мала, число независимых испытаний достаточно велико, но значение произведения остается небольшим (не больше десяти), то вероятность того, что в этих испытаниях событие наступит раз, Для упрощения расчетов с применением формулы Пуассона составлена таблица значений функции Пуассона (см. прил. 3). Пример 6. Пусть вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных. Решение. Здесь Найдем вероятность того же события по формуле Лапласа. Для этого сначала вычисляем значение , соответствующее : Поэтому согласно формуле Лапласа искомая вероятность а согласно формуле Бернулли точное ее значение Таким образом, относительная ошибка вычисления вероятностей по приближенной формуле Лапласа составляет а по формуле Пуассона — т. е. во много раз меньше. |

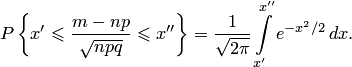 (3.6)
(3.6)