Гидравлика Экзамен. 1. Определение гидравлики. Основные понятия и определения. Сплошная среда. Гидравликой

• Название: 1. Определение гидравлики. Основные понятия и определения. Сплошная среда. Гидравликой
• Анкор: Гидравлика Экзамен.doc
• Дата: 26.04.2017
• Размер: 2.14 Mb.
• Имя файла: Гидравлика Экзамен.doc
• Тип: Документы; #5498
• страница: 3 из 4

3) Расходомер Вентури.

Расходомер Вентури (рис ниже) представляет собой сужение, или горло, в тракте трубопровода постоянного сечения. В горле скорость возрастает, а давление соответственно уменьшается. Разность статических давлений на входе и в горле регистрируется дифференциальным манометром, и расход жидкости определяется по формуле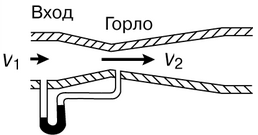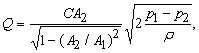



где Q – объемный расход жидкости, измеряемый в м³/с, А₁ и А₂ – площади поперечных сечений на входе и в горле соответственно, r – плотность жидкости, (p₁ – p₂) – разность статических давлений на входе и в горле и С– определяемый экспериментально коэффициент расходомерного насадка, принимающий значения, как правило, от 0,95 до 0,99. Введение коэффициента насадка отражает потери давления внутри расходомера.

Выходной (расширяющийся) конус трубы Вентури предназначен для расширения проходного сечения потока до прежнего значения. Суммарные потери давления в трубе Вентури составляют от 5 до 20%.

4) Формула Торричелли

Закон Торричелли показывает, что при истечении идеальной нестискувальнои жидкости из щели в боковой стенке или на дне сосуда жидкость приобретает скорость тела, падающего с определенной высоты. С помощью этого можно вычислить максимальный уровень утечки жидкости из сосуда. Для подтверждения можно воспользоваться законом Бернулли, выведя из него формулу Торричелли: ρgh + p ₀ = (pV ²⁾ / 2 + p _0, где p0 - атмосферное давление, h - высота столба жидкости в сосуде, V - скорость истечения жидкости. Отсюда V = √ 2gh.

5) Пульверизатор

В пульверизаторе применяется главный следствие закона Бернулли: с ростом скорости происходит рост динамического давления и падение статического давления. В капилляры пульверизатора вдувается воздух или пар. Вдувание снижает атмосферное давление в капилляре, и жидкость из баллона пульверизатора под действием большего атмосферного давления поднимается капилляром. Там она раздробляется струей воздуха.

6) Водоструйный насос

Водоструйный насос - резервуар, в который впаяны две трубки. Под действием давления в первую трубку протекает вода, попадая затем в другую трубку. В суженной части первой трубки возникает уменьшен давление, меньше атмосферного. Поэтому в резервуаре создается напряжение. Трубку подсоединяют к резервуару, который проходит в сосуд, из которого необходимо откачать воздух.

7)Ракета

В конструировании ракет также применяется закон Бернулли. Для создания тяги в ракете используется топливо, которое сжигают в камере сгорания. Газы образуют реактивную струю, который ускоряется, проходя через специальное сужение - сопло. Именно сужение сопла и является основной причиной ускорения реактивной струи газов и увеличения реактивной тяги.

8) Свисток Свисток представляет собой пример использования закона Бернулли в газоструменевих излучателях звуковых волн. Вихревой свисток представляет собой цилиндрическую камеру, в подается поток воздуха через тангенциально расположенную трубку. Образовавшийся вихревой поток поступает в выходную трубку меньшего диаметра, расположенной на оси. Там интенсивность вихря резко повышается и давление в его центре становится значительно ниже атмосферного. Перепад давления периодически выравнивается за счет прорыва газов из атмосферы в выходную трубку и разрушения вихря.
32. Классификация гидравлических потерь

Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной.

Гидравлические потери принято разделять на два вида:

1) Потери на трение по длине- это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают прямо пропорционально длине трубы . Рассматриваемые потери обусловлены внутренним трением жидкости в трубах. Потери напора при трении определяются по формуле Дарси-Вейсбаха

где λ – коэффициент гидравлического трения по длине или коэффициент Дарси; l – длина трубопровода; d–его диаметр; V – средняя скорость течения жидкости.

2) Местные потери напора h_м - обусловлены местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. , и определяются по формуле Вейсбаха

, где V-средняя скорость в трубе;-коэффициент местного сопротивления.
33.Структура потока в области местных сопротивлений

Простейшие местные гидравлические сопротивления можно раз­делить на расширения, сужения и повороты русла, каждое из ко­торых может быть внезапным или постепенным. Более сложные слу­чаи местных сопротивлений представляют собой соединения или комбинации перечисленных простейших сопротивлений. Так, напри­мер, при течении жидкости через вентиль поток ис­кривляется, меняет свое направление, сужается и, наконец, расширя­ется до первоначальных размеров; при этом возникают интенсивные вихреобразования.

1) При внезапном расширении потока в трубке от сечения 1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот.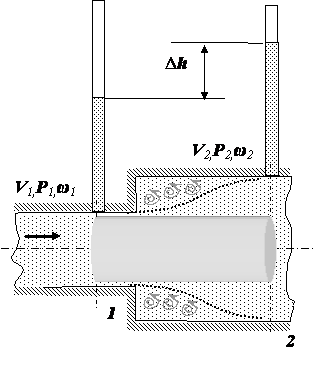



Назвав разность потерянной скоростью, можно сказать, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.

2) При внезапном сужении, так же как и при внезапном расширении потока, создаются пространства с завихрениями вращающейся жидкости, которые образуются в пристенном пространстве широкой части трубы. Такие же завихрения образуются в начале узкой части трубы за счёт того, что при входе в неё (узкую часть) жидкость продолжает некоторое время двигаться по инерции в направлении центра трубы, и основное русло потока ещё некоторое время продолжает сужаться. Следовательно, при внезапном сужении потока возникает как - бы два подряд идущих местных сопротивления. Местное сопротивление за счёт сужения основного русла и сразу же за ним местное расширение, уже рассмотренное выше. С учётом этого потери напора при внезапном сужении примут вид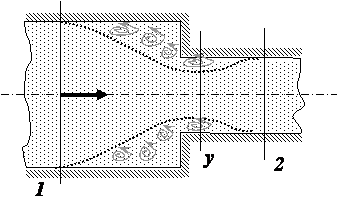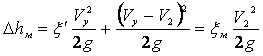



3) Постепенное расширение трубы называется диффузором. Движение жидкости в диффузоре сопровождается уменьшением скорости и повышением давления. Частицы жидкости движутся вперёд, в сторону более высокого давления, по инерции за счёт своей кинетической энергии, которая уменьшается по направлению движения. Кроме того, за счёт расширения трубы частицы жидкости движутся не только вдоль оси потока, но и в направлении от оси к стенкам. В каком-то сечении инерция жидкости уменьшается до такой степени, что её не хватает для преодоления повышающегося давления. Тогда такие частицы жидкости останавливаются или даже начинают двигаться в обратном направлении. В результате возникают вихревые потоки и потоки, отрывающиеся от стенки. Эти явления зависят от скорости и интенсивности расширения потока. Кроме того, в диффузоре происходят обычные потери на трение, подобные потерям по длине в трубах постоянного сечения. Таким образом, потери энергии в диффузоре складываются из потерь на трение по длине и потерь на вихреобразование за счёт расширения: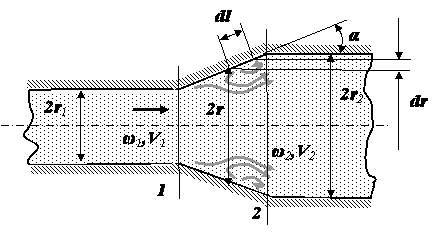

.

Окончательно формула для определения потерь напора в диффузоре примет вид



4) Постепенное сужение потока - такое сопротивление представляет собой коническую сходящуюся трубку – конфузор. Течение в конфузоре сопровождается постепенным увеличением скорости и одновременным снижением давления. По этой причине условия для вихреобразования на конической поверхности отсутствуют. Потери в этой части местного сопротивления происходят только за счёт трения. Вихреобразование может происходить только в узкой части трубы. Его природа аналогична природе подобного вихря при внезапном сужении потока, однако величина существенно меньше. В большинстве работ по гидравлике указывается, что эта величина столь незначительна по сравнению с потерями на трение в конической части конфузора, что ею можно пренебречь. С учётом сказанного, величину этих потерь можно определить по формуле, вывод которой аналогичен выводу формулы потерь на трение в диффузоре. Она имеет вид: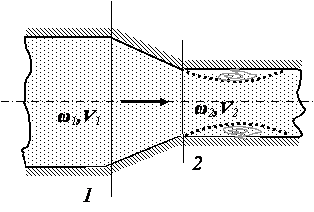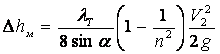



5) Внезапный поворот потока - такое местное сопротивление, называемое обычно коленом, очень сильно влияет на потери напора. В нём происходит отрыв потока от стенки трубы и создаются две сложные вихревые зоны, в которых интенсивно теряется энергия. Степень интенсивности существенно зависит от угла поворота . Коэффициент местного сопротивления значительно возрастает с увеличением угла поворота, и его можно определить по эмпирической формуле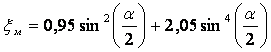

.

В гидросистемах подобных местных сопротивлений рекомендуется избегать.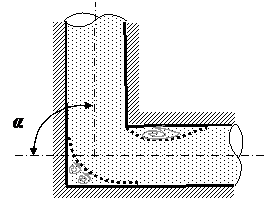



6) Плавный поворот потока - постепенный поворот трубы (отвод или закруглённое колено) значительно уменьшает вихреобразование и, следовательно, потери энергии. Величина потерь существенно зависит от отношения R/d и угла .

Коэффициент местного сопротивления для плавного поворота можно определить по экспериментальным формулам. Для поворота под углом 90⁰ и (R / d) >1 он равен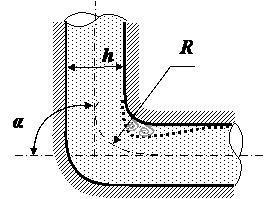

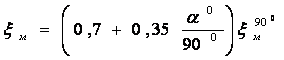;для угла поворота более 100⁰

;для угла поворота менее 70⁰

.

34. Эквивалентная длина

Эквивалентной длиной называют такую длину прямого участка трубопровода данного диаметра, потери напора в котором при пропуске данного расхода равны рассматриваемым местным потерям.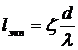

, получаем .

Эквивалентной длинойданного местного сопротивления называют такую длину прямого отрезка трубы, которая создает гидравлическое сопротивление, равное сопротивлению детали трубопровода, обусловившей потери напора.

35. Режимы движения жидкости. Основные понятия. Критерий Рейнольдса

1) Ламинарнымназывается слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При таком течении все линии тока жидкости вполне определяются формой русла. При ламинарном течении в трубе все линии тока направлены параллельно оси трубы. Ламинарное течение является упорядоченным при постоянном напоре строго установившегося течения. Ламинарный режим наблюдается преимущественно при движении вязких жидкостей (нефти, смазочных масел и т.п.), и менее вязких жидкостей при их течении с небольшими скоростями.

2) Турбулентнымназывается течение, сопровождающееся интенсивным перемешиванием жидкости и пульсацией скоростей и давления. Движение отдельных частиц оказывается хаотичным, беспорядочным. Наряду с осевым перемещением наблюдается вращательное и поперечное перемещение отдельных объемов жидкости. Этим и объясняются пульсации скоростей и давления.

- Безразмерный комплекс величин , значение которого позволяет судить о режиме движения жидкости, называется критериемРейнольдса(Re)

При режим движения жидкости будет ламинарным. При Re>3000 режим турбулентный. При 2300 ≤ Re ≤ 3000 переходный режим.

Если жидкость движется по трубе круглого сечения, то в формулу (чуть выше) подставляют внутренний диаметр трубы . Если жидкость движется по каналу некруглого сечения, то подставляют, так называемый, эквивалентный диаметр , равный отношению учетверённой площади сечения потока к смоченному периметру канала: d_э= 4F / П.
36. Основное уравнение равномерного движения

Рассмотрим прямолинейное равномерное движение жидкости. Живые сечения в этом случае могут быть произвольной формы, но не должны изменяться по всей длине рассматриваемого участка. В таком потоке потери напора определяются лишь потерями по длине.

Выделим из потока участок жидкости длиной l и запишем уравнение Бернулли для сечений 1 и 2( рис. 32 )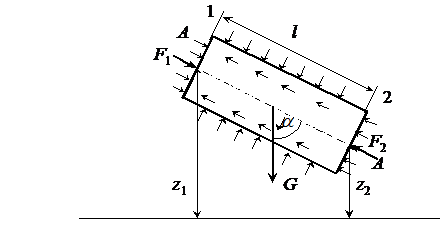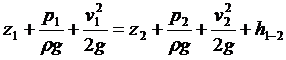



где z1 , z2 - ординаты центра тяжести сечений 1,2; p1 , p2 - давление в центрах тяжести этих сечений,

v1 , v2 - средние скорости в этих сечениях, h1-2 - потери напора по длине.

Так как движение равномерное, то v1 =v2 и уравнение можно переписать так: .

Для вычисления этой разности напишем сумму проекций на ось А-А всех сил, действующих на участке 1-2. Эти силы следующие:

1) сила тяжести жидкости

2) силы давления на плоские сечения , , ,

3) сила трения ,

где t - сила трения на единицу площади смачиваемой поверхности русла, c - смоченный периметр,

4) силы давления стенок на жидкость ( эти силы не подсчитываем, так как они параллельны оси А-Аи, следовательно, их проекции на ось А-А равны нулю ). Спроектируем все эти силы на ось А-А: Из рисунка .

Подставим выражение для сил в уравнение .

Разделим обе части этого равенства на , имеем

Сравнивая выражения, находим 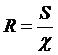, откуда . Отношение площади живого сечения S к смоченному периметру c называется гидравлическим радиусом

. Величина обозначается через i и называется гидравлическим уклоном. Получаем - Это уравнение называется основным уравнением равномерного движения.

37. Эпюры скоростей при ламинарном и турбулентном режимах движения жидкости

1) При ламинарном движении наибольшая скорость развивается в центре трубы, наименьшая - у стенок.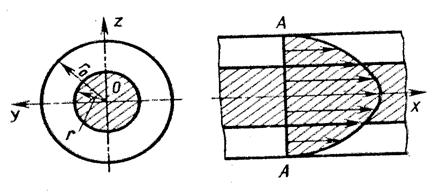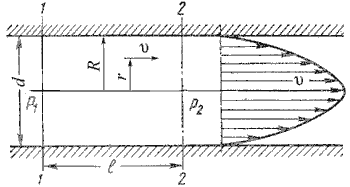

2) При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рисунке ниже. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.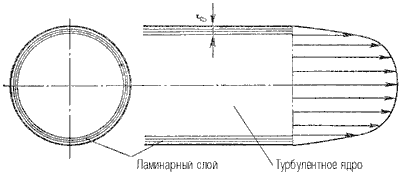



38. Определение эквивалентной шероховатости. Гидравлически гладкие и шероховатые поверхности

1) Эквивалентная шероховатость называется абсолютная равномерная шероховатость, которая вызывает также гидравлические потери, как и шероховатость на реальной стенке трубы. Обозначается К_Э или Δ_Э.

( Равномерной называется шероховатость, имеющая одинаковую высоту выступов, находящихся на одинаковом расстоянии друг от друга. В природе такая шероховатость не существует. Её можно создать только искусственно. Если поверхность труб и открытых лотков покрыта специально отсортированными зёрнами песка одной фракции, то шероховатость получается равнозернистая и равномерно расположенная по поверхности стенки; Абсолютная шероховатость полностью не может характеризовать гидравлическое сопротивление стенки, так как одна и та же её величина в "тонкой" трубе имеет большее значение, чем в "толстой". Поэтому вводится понятие относительной шероховатости, являющейся отношением эквивалентной шероховатости к диаметру трубы К_Э/d или Δ_Э /d. Или к радиусу К_Э /r или Δ_Э /r. Величина, обратная относительной шероховатости называется относительной гладкостью трубы d /К_Э или d/ Δ_Э.)

2) Если толщина вязкого подслоя δ_b превышает толщину абсолютной шероховатости Δ (δ_b > Δ), то все неровности полностью погружены в ламинарную пленку. Ядро потока как бы катится по пленке, не чувствуя шероховатости стенок. В этом случае шероховатость стенок не влияет на особенности движения ядра потока и, соответственно, потери напора не зависят от пристенной шероховатости. Такие поверхности условно называют гидравлически гладкими.

3) Если высота выступов шероховатости Δ превышает толщину вязкого подслоя (Δ > δ_b), нервности стенок выходят в пределы турбулентного ядра. Поток обтекает выступы с отрывом, сопровождающимся порождением мелкомасштабных вихрей и интенсивным перемешиванием частиц. В этом случае потери напора на трение сильно возрастают и уже зависят от шероховатости. Такие трубы поверхности называются гидравлически шероховатыми.

39.Метод наложения потерь. Коэффициент сопротивления системы

метод наложения потерь применим только в тех случаях, когда местные сопротивления расположены друг от друга на таких расстояниях, при которых движение жидкости в трубопроводе до места следующего сопротивления успевает установиться, а эпюра распределения скоростей в трубопроводе успевает приобрести обычную форму, присущую данному ввиду движения.